Fracciones equivalentes

Las fracciones

En este sentido, será necesario comenzar a decir entonces que las fracciones pueden ser consideradas como una de las expresiones que pueden tener los números fraccionarios, encontrándose constituida entonces por la división de dos números enteros. Así también, las Matemáticas indican que dentro de las fracciones podrán encontrarse dos elementos, cada uno de los cuales ha sido descrito de la siguiente manera:

• Numerador: en primer lugar, se encontrará el Numerador, el cual estará constituido por el número que se ubica en la parte superior de la fracción, y que cumplirá con la función de señalar cuál es la parte del todo que representa la fracción.
• Denominador: por su parte, el Denominador ocupará la posición inferior de la fracción, y tendrá la tarea de dar cuenta del todo, del que la fracción es solo una porción.

Fracciones equivalentes

Teniendo presente esta definición, puede entonces que sea mucho más sencillo entender la noción de Fracciones equivalentes, las cuales básicamente han sido explicadas por las Matemáticas como aquellas fracciones, que pese a tener valores distintos en cuanto a sus numeradores y denominadores, en realidad representan la misma parte del todo, es decir, que más allá de sus aparentes diferencias, en realidad dan cuenta del mismo valor.

No obstante, puede que lo mejor para garantizar la total comprensión de este concepto, sea recurrir a un ejemplo gráfico, en el cual pueda verse claramente cómo dos fracciones, aun cuando no expresen iguales valores en sus elementos, en realidad son equivalentes por representar la misma porción, tal como se muestra a continuación:

Si se quisiera comprobar gráficamente que ambas fracciones son equivalentes, se deberían dibujar lo que representa cada una de ellas:

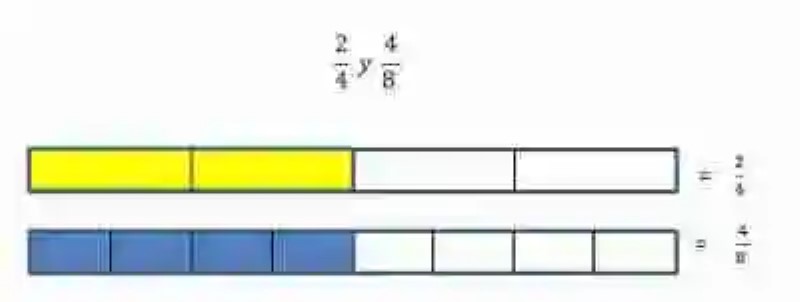
Al hacerlo, se podrá ver cómo aun cuando el todo esté dividido de forma distinta, y las porciones parecieran apuntar a valores distintos, en realidad son equivalentes, puesto que tienen igual valor.

Cómo determinar si dos fracciones son equivalentes

Sin embargo, no siempre se podrá recorrer al recurso gráfico toda vez que se quiera determinar si realmente el valor de las fracciones resulta equivalente, sino que se podrá hacer uso de la operación de la multiplicación cruzada, lo cual se usará en todos los casos, es decir, tanto si las fracciones resultan positivas o negativas. Esta operación podrá representarse de la siguiente manera:

Ejemplo de cómo determinar si dos fracciones son equivalentes

No obstante, puede que todavía sea necesario un ejemplo en donde se pueda ver de forma práctica la forma de determinar si dos fracciones, pese a expresar valores distintos, pueden referir a la misma porción, es decir, ser equivalentes, tal como el que se muestra a continuación:

Determinar si las siguientes fracciones son equivalentes:

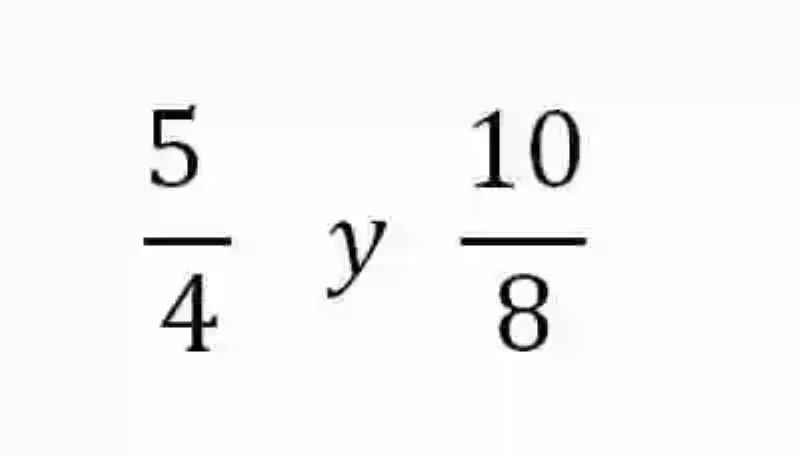
Para cumplir con lo solicitado por el postulado, será necesario comenzar a realizar una operación de multiplicación cruzada, en la cual el numerador de la primera fracción, se multiplica con el denominador de la segunda expresión, y así mismo el denominador de la primera fracción, se multiplicará por el numerador de la segunda fracción. Si estas fracciones son equivalentes, entonces ambos productos obtenidos contarán con iguales valores:

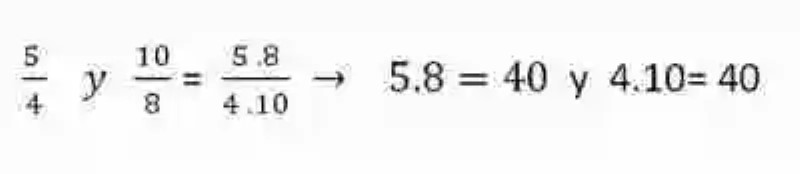
Tal como dice la teoría, la multiplicación cruzada de estas fracciones originan iguales resultados, por lo que entonces se asume que estas son fracciones equivalentes.

Imagen: pixabay.com