
Tal vez lo mejor, antes de avanzar sobre una definición respecto a las Fracciones propias, sea necesario hacer una breve revisión sobre algunos conceptos, que permitirán entender este tipo de fracción dentro de su contexto preciso.
Definiciones fundamentales
En este orden de ideas, quizás sea necesario centrar la atención entonces en tres definiciones específicas: Números racionales, Números fraccionarios, numerador y denominador, por ser estos los conceptos directamente relacionados a la naturaleza de las fracciones denominadas fracciones propias. A continuación, cada una de estas definiciones:
Números racionales
En primer lugar, se encontrarán los Números racionales, entendidos como aquellos elementos, distintos a cero, conformados tanto por números enteros como por números fraccionarios, los cuales son expresados en forma de fracción. Así mismo, estos números son considerados como aquellos elementos numéricos que componen el conjunto numérico Q, el cual cuenta con los números enteros como uno de sus subconjuntos, mientras que ella misma como colección es vista como un subconjunto de los Números reales.
Números fraccionarios
Por otro lado, los Números fraccionarios serán aquellos elementos numéricos usados para representar cantidades no enteras o exactas, las cuales serán representadas de dos formas posibles, bien a través de una fracción, en donde se verá tanto un numerador como un denominador, así también como a través de una expresión decimal, constituida por un número mixto, en el cual se puedan encontrar tanto números enteros como decimales. Estos números serán asumidos como un subconjunto de los Números racionales, es decir, del conjunto Q.
Numerador
Así también será de gran importancia lanzar luces sobre el concepto de Numerador, el cual es entendido por las distintas fuentes matemáticas como el elemento que se ubica en la parte superior de la fracción, y que cumple con la función de señalar cuál es el número entero o natural en el que quiere averiguarse cuántas veces se encuentran contenido el denominador. Debe ser un número distinto al cero, y siendo entero, pues puede ser tanto positivo como negativo.
Denominador
Por último, el Denominador será identificado como el elemento que se ubicará por debajo del denominador, a fin de señalar cuál es el número que debe determinarse cuántas veces se encuentra contenido por el numerador, es decir, que siendo distinto a cero, será el número que se usará para dividir el numerador.
Fracciones propias
Teniendo presente estas definiciones, quizás entonces sea mucho más sencillo abordar el concepto de fracciones propias, las cuales han sido explicadas por las Matemáticas como un tipo de fracción, caracterizada por contar con un numerador, que siendo distinto a cero, está constituido por un número que resulta mayor que el denominador. Algunos ejemplos de esta clase de fracciones son las siguientes:
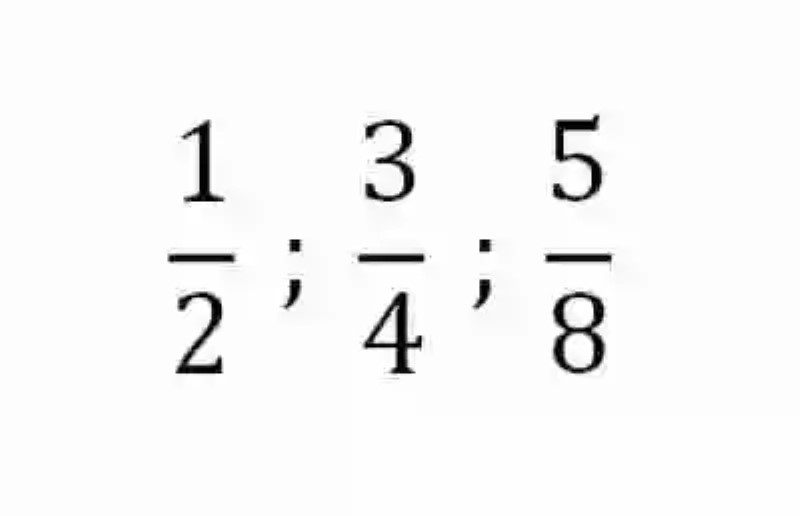
Cuando estas fracciones son llevadas a su expresión decimal dan como resultados números mixtos, en donde se puede ver como número entero al cero, y como decimales a otros números naturales. En cuanto a su ubicación en la Recta numérica, estas fracciones propias suelen encontrarse en algún lugar entre el 0 y el 1, o incluso, si en ella han participado números enteros negativos, también podrán encontrarse entre el 0 y el -1.
Imagen: pixabay.com
El pensante.com (diciembre 14, 2017). Fracciones propias. Recuperado de https://elpensante.com/fracciones-propias/