
Entre los distintos tipos de funciones matemáticas que existen, se encuentra la función Afín. Sin embargo, previo a avanzar en una explicación sobre este tipo de relación matemática, se estudiarán algunas definiciones, que de seguro permitirán entenderla dentro de su justo contexto matemático.
Definiciones fundamentales
En este sentido, se tomará igualmente la decisión de delimitar esta revisión teórica a cuatro nociones específicas: Conjuntos, Correspondencia, Funciones y Variables de la función, por encontrarse directamente relacionados con el tipo de función que se estudiará posteriormente. A continuación, cada una de estas definiciones:
Los conjuntos
Por consiguiente, podrá verse que las Matemáticas definen los Conjuntos como un objeto matemático, constituido por un grupo de elementos, que se caracterizan por responder a la misma naturaleza, de ahí que algunos autores señalan que los Conjuntos pueden ser entendidos también como colecciones abstractas de elementos heterogéneos.
Así mismo, la disciplina matemática ha señalado que los elementos del conjunto se caracterizan igualmente por contar con la capacidad de determinar la colección a la cual pertenecen de forma única y exclusiva. Por otro lado, los diferentes autores han señalado que los Conjuntos se deben expresar de la siguiente manera: ser denominados por una letra mayúscula, por su parte los elementos deberán ser presentados como una enumeración, separados por comas y comprendidos entre signos de llaves: { }
Correspondencia
Igualmente, será necesario revisar el concepto de Correspondencia, el cual ha sido explicado como un tipo de relación matemática, la cual ocurre entre dos conjuntos, siempre que uno, alguno o todos los elementos de una de estas colecciones encuentren en uno, alguno o todos los elementos de la otra colección, y según un criterio específico, una determinada correspondencia. Un ejemplo de este tipo de relación entre conjuntos será el siguiente:
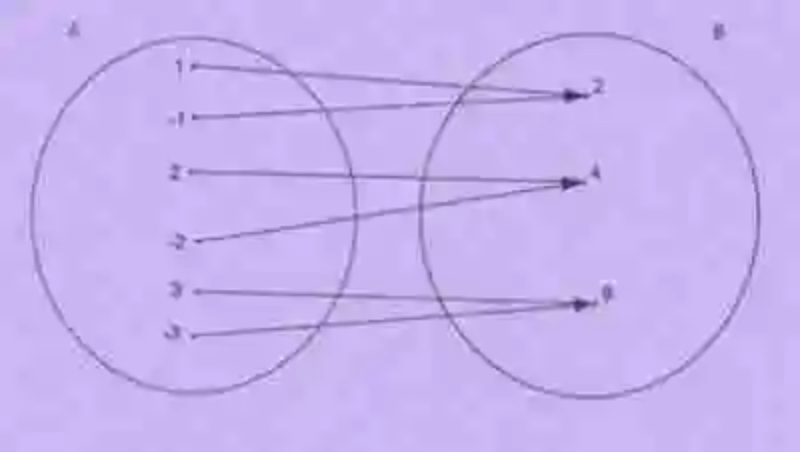
Por otro lado, los diferentes autores han indicado que en la Correspondencia, además de los conjuntos relacionados, se puede hablar de tres distintas colecciones, cada una de las cuales han sido descritas de la siguiente forma:
- Conjunto de inicio: también conocido como conjunto de partida o inicial, esta colección se caracteriza por encontrarse conformada por todos los elementos que se encuentran relacionados con los del siguiente conjunto. Estos elementos son denominados por su parte elementos antiimagen, y cumplen con la tarea de ejercer como primer elementos del par de correspondencia. Así también, las Matemáticas han explicado este conjunto como la colección de la cual parte la correspondencia, al igual que las flechas que indican la relación. V
- Conjunto final: igualmente, en la Correspondencia, podrá encontrarse el Conjunto final, conocido también como el Conjunto de llegada, el cual es definido como la colección en donde desemboca la correspondencia, al igual que las flechas que la señalan. Con respecto a sus elementos, estos estarán constituidos por aquellos que sirvan de imagen a los elementos de la primera colección. Estos elementos además fungirán como el segundo término del par de correspondencia.
- Grafo: por último, en la relación de Correspondencia, existirá también el Grafo, el cual ha sido explicado como el conjunto que se crea en base a los distintos pares de correspondencia, que se establecen entre los elementos del Conjunto inicial y los elementos del Conjunto final, que se encuentran relacionados entre sí.
Función
Otra de las definiciones sobre la cual deberán lanzarse luces en la de Función, la cual ha sido explicada por los distintos autores como una relación de correspondencia, que sucede entre dos conjuntos, siempre que los elementos del conjunto de inicio cuenten con una sola imagen entre los elementos del conjunto de llega. Un ejemplo de este tipo de relación puede ser el siguiente:
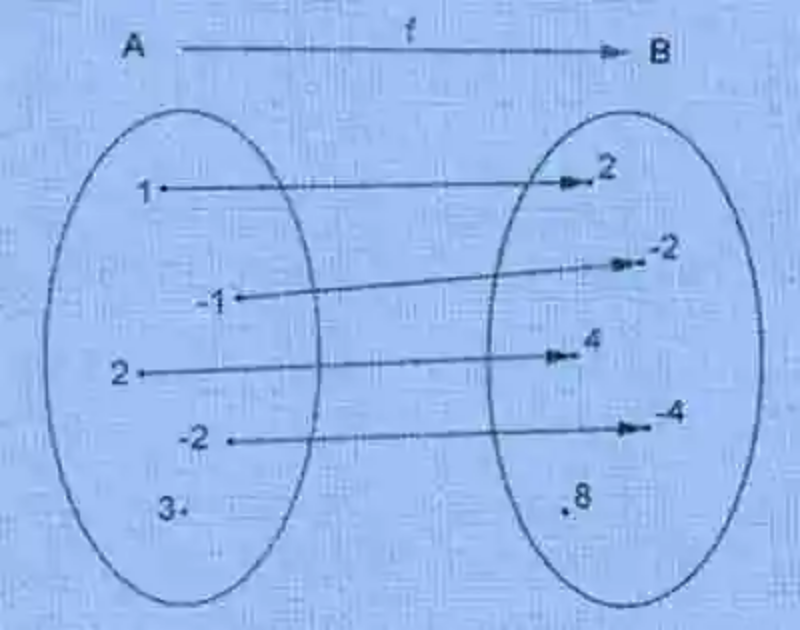
Variables de la Función
Además, las Matemáticas señalan que en la Función pueden distinguirse dos distintas variables, cada una de las cuales han sido explicadas de la siguiente forma:
- Variable independiente: esta variable también es conocida como variable x, y se caracteriza por tener un valor, que no depende de otra variable. Su función es someterse a la ecuación de la función, para determinar que valor tiene y cuando x presenta cierta cantidad.
- Valor dependiente: por otro lado, en la Función también se encuentra la Variable dependiente, la cual es conocida como Variable y. Su valor depende totalmente o se encuentra en función de x. Para determinarlo, es necesario resolver la ecuación de la función.
Función afín
Una vez se han revisado estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre la Función afín, la cual ha sido explicada como la situación matemática en la que dos o más funciones presentan características o propiedades similares, por lo que entonces se dice que estas tienen afinidad entre sí.
Además, la disciplina matemática señala que las funciones afines se identifican tomando en cuenta algunas de las siguientes posibles características:
1.- En primer lugar, todas las funciones afines responden a la ecuación o forma y = mx + b, en donde independientemente del valor que tome b, el sumando mx es común a todas las funciones que pueden considerarse afines entre sí.
2.- Otra característica importante de las Funciones afines es que todas son funciones lineales.
3.- Por último, entre las funciones lineales puede encontrarse también que todas cuentan con la misma pendiente de recta.
Imagen: pixabay.com
El pensante.com (marzo 30, 2019). Función afín. Recuperado de https://elpensante.com/funcion-afin/