Funciones de variable entera

Definiciones fundamentales

De esta forma, puede que también sea necesario enfocar esta revisión teórica a cuatro nociones específicas: Números enteros, Conjuntos, Correspondencias entre conjuntos, Funciones, así también como las definiciones de Dominio y Rango. A continuación, cada uno de estos conceptos:

Los números enteros

En primer lugar, se centrará la atención entonces en el concepto de Números enteros, los cuales han sido explicados como aquellos elementos numéricos, que pueden considerarse como parte de un conjunto, en donde hacen parte los números naturales, sus opuestos negativos y el cero. La colección conformada por este tipo de números se designa con la letra ℤ. Así mismo, estos números son reconocidos como aquellos elementos numéricos que expresan una cantidad completa, no fraccionaria, o la ausencia de ella.

Conjuntos matemáticos

Por otro lado, será igualmente conveniente detenerse un momento en la definición de Conjuntos matemáticos, los cuales han sido explicados como objetos que se constituyen en base a la reunión de una serie de elementos, cuya principal característica es la de pertenecer o poder considerarse pertenecientes a la misma naturaleza.

Igualmente, las distintas fuentes señalan que los elementos que conforman los conjuntos matemáticos cuentan con la capacidad de determinar, de forma única y exclusiva, las colecciones que constituye. Con respecto a la forma correcta en que debe ser expresado un conjunto, las Matemáticas señalan que este tipo de colecciones deberán ser siempre denominadas por medio de una letra mayúscula, mientras que sus elementos deberán presentarse como una numeración, siendo separados por comas, al tiempo que van incluidos entre signos de llaves: { }

Correspondencia

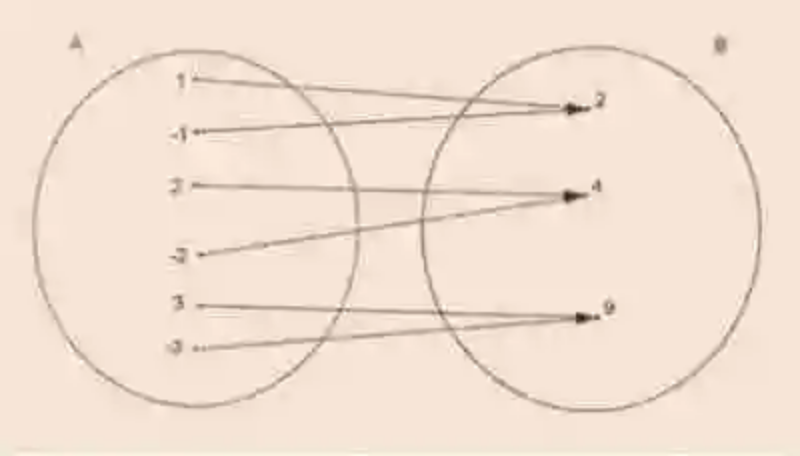
Otro de las definiciones que deben tenerse en cuenta durante esta revisión teórica es el de Correspondencia entre conjuntos, la cual ha sido definido entonces como la relación matemática que se da entre dos conjuntos, siempre que uno, algunos o todos los elementos de una colección encuentren correspondencia, según un criterio específico, en uno, algunos o todos los elementos de la segunda colección. Un ejemplo de este tipo de relación podrá ser la siguiente:

Además, en las relaciones de Correspondencia, se encontrarán tres distintos conjuntos o colecciones, las cuales pueden ser explicadas de la siguiente manera:

• Conjunto inicial: conocido también como Conjunto de partida, se caracteriza por ser la colección de la cual parte o se origina la correspondencia, así como el conjunto de donde parten las flechas que señalan esta relación. En cuanto a los elementos que pertenecen a este conjunto, las Matemáticas señalan que aquellos que participan de la Correspondencia reciben el nombre de elementos antiimagen, mientras que reciben la responsabilidad de ejercer como primer miembro del par de correspondencia. En el ejemplo usado para ilustrar esta relación, se puede establecer que el conjunto inicial es el siguiente: A = {1, -1, 2, -2, 3, -3}
• Conjunto de llegada: por su parte, en la Correspondencia también hará parte el Conjunto de llegada, o Conjunto final, el cual se caracterizará por ser la colección en la cual desembocan las flechas que señalan la Correspondencia. En cuanto a sus elementos, aquellos que participen de la relación recibirán el nombre de elementos imagen, al tiempo que fungirán como segundo elemento en el par de correspondencia. En el ejemplo empleado se tendrá el siguiente conjunto final: B= {2, 4, 9}
• Grafo: por último, en las relaciones de Correspondencia también se encontrará el Grafo, el cual es definido como la colección o conjunto conformado entonces por los distintos pares de correspondencia, que se han formado según el criterio de correspondencia por medio del cual se han relacionado las dos colecciones. En este caso en específico, es decir, en relación con este ejemplo, el Grafo será el siguiente: G = {(1, 2), (-1, 2), (2, 4), (-2, 4), (3, 9), (-3, 9)}

Función

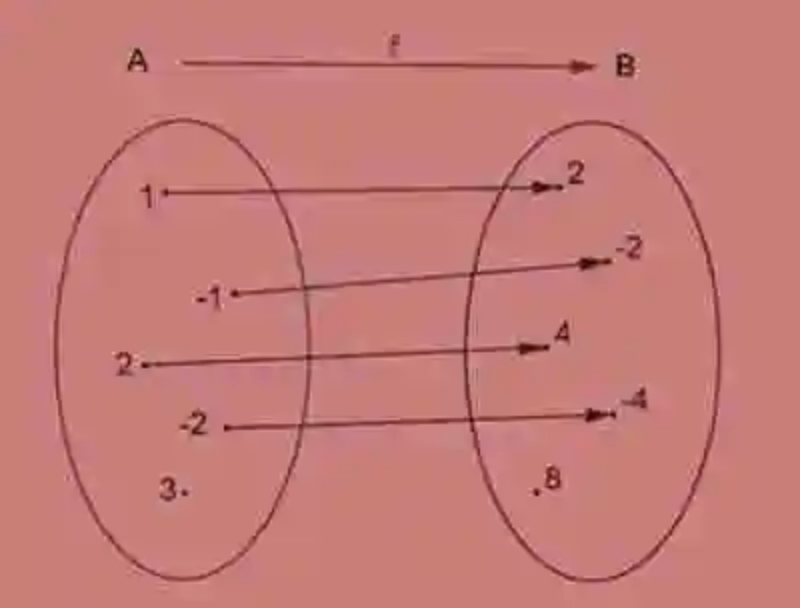
De igual forma, será necesario pasar revista sobre el concepto de Función, la cual ha sido explicada entonces como la relación matemática de correspondencia que existe entre dos conjuntos, siempre que los elementos del conjunto inicial que participan de la relación cuenten con solo una imagen en los elementos que constituyen el conjunto final. Un ejemplo de este tipo de relación será el siguiente:

Por igual, en las funciones matemáticas podrán distinguirse dos distintos tipos de variables, las cuales han sido explicadas de la siguiente manera:

• Variables independientes: este tipo de variables serán bautizadas o identificadas siempre por la letra x, y su valor puede ser asignado aleatoriamente, constituyendo el conjunto inicial.
• Variables dependientes: por otro lado, en las Funciones también podrán encontrarse las variables dependientes, las cuales serán bautizadas por el nombre de y, siendo su valor definida por la ecuación de la función, de la cual participa el valor de x, así como el criterio de correspondencia por medio del cual se ha conformado la función.

Dominio y recorrido de una función

Por último, también será necesario traer a capítulo los conceptos de Dominio y Rango de una función. Al respecto también es imprescindible con recordar que para que exista una Función es necesario que todos los elementos del conjunto inicial que encuentran correspondencia en el conjunto final cuenten con una sola imagen, lo cual no quiere decir entonces que todos los elementos del conjunto inicial y todos los elementos del conjunto final deban encontrarse relacionados necesariamente. Es acá cuando surgen entonces los conceptos de Dominio y Rango, los cuales han sido explicados de la siguiente forma:

• Dominio: será entendida entonces como la colección o conjunto, constituido por los elementos del conjunto inicial de una función que participan necesariamente de la relación.
• Rango: por su lado, el Rango de una Función matemática se encontrará constituido por la totalidad de elementos que sirven de imagen a los elementos del conjunto inicial, que hacen parte de la relación.

Función de variable entera

Una vez se han revisado cada uno de estos distintos conceptos, puede que ciertamente sea mucho más sencillo aproximarse a la definición de Función de variable entera, la cual básicamente podrá ser definida como la relación de correspondencia matemática que existe entre dos conjuntos, toda vez que los elementos del conjunto inicial cuentan en el conjunto final con una sola imagen, y los elementos que constituyen el Dominio de la Función pertenecen por completo al conjunto de los números enteros, es decir, que son números naturales, sus opuestos negativos o el cero.

Por ende, siempre que el Dominio de la Función esté constituido por números enteros, entonces se dirá que se está ante una Función de variable entera. Un ejemplo de este tipo de Función matemática será el siguiente:

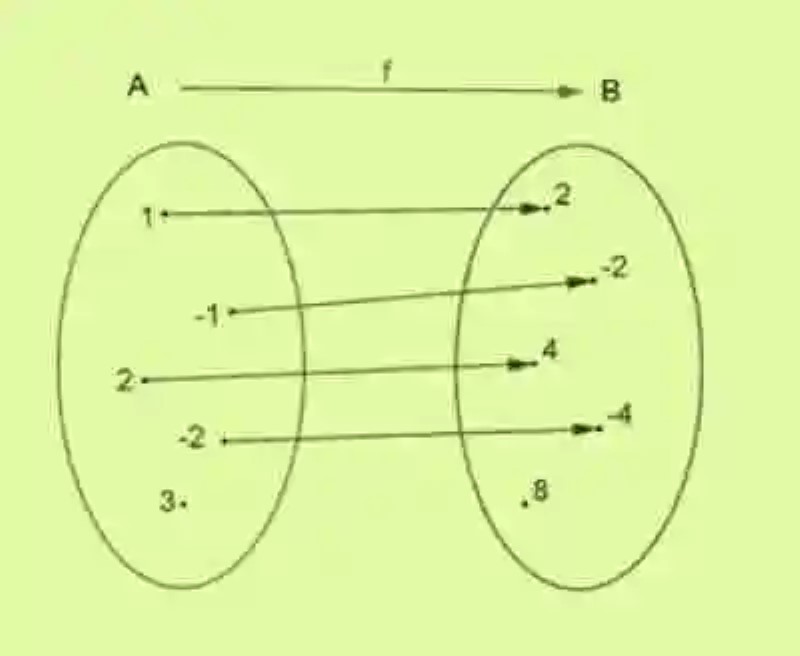
Imagen: pixabay.com