Funciones de variable racional

Definiciones fundamentales

En este sentido, se optará también por delimitar esta revisión teórica a cinco nociones específicas: Números racionales, Conjuntos matemáticos, Correspondencia entre conjuntos, Funciones, así como los conceptos de Dominio y Rango de una función. A continuación, cada una de estas definiciones:

Los números racionales

De esta manera, podrá comenzarse por decir que las Matemáticas han explicado los Números racionales como todos aquellos elementos abstractos numéricos, que cuentan con la propiedad de presentarse como el cociente entre dos números enteros, siempre que el número que sirve de dividendo sea un número entero, y el divisor sea un número natural positivo.

Así mismo, la disciplina matemática ha señalado que este conjunto numérico se denota con la letra Q, al tiempo que es considerado como un subconjunto de los números Reales (ℝ), mientras que él mismo cuenta con la capacidad de contener los Números enteros (ℤ).

Conjuntos matemáticos

En segunda instancia, será también prudente lanzar luces sobre la definición de Conjuntos matemáticos, los cuales han sido explicados entonces como un objeto matemático, constituido en base a un grupo de elementos, cuya principal característica es la de responder a la misma naturaleza, de ahí entonces que los Conjuntos también hayan sido explicados como colecciones abstractas y homogéneas.

Así mismo, las distintas fuentes han señalado que los Conjuntos matemáticos se caracterizan por contar con elementos, que tienen la capacidad de definir, esta clase de colecciones, de una forma única y exclusiva. En relación con la manera en que deben expresarse este tipo de conjuntos, las Matemáticas señalan que estos objetos deberán ser siempre bautizados por una letra mayúscula, mientras que sus elementos deberán presentarse como una enumeración de objetos, separados por comas, e incluidos entre signos de comas: { }

Correspondencia entre conjuntos

Otro de los conceptos que deben ser abordados será el de Correspondencia entre conjuntos, los cuales han sido explicados como la relación matemática que existe entre dos colecciones de elementos, siempre que uno, algunos o todos los elementos de un conjunto, según un criterio específico, encuentren relación o correspondencia con los elementos de la otra colección involucrada. Un ejemplo de Correspondencia entre conjuntos será el siguiente:

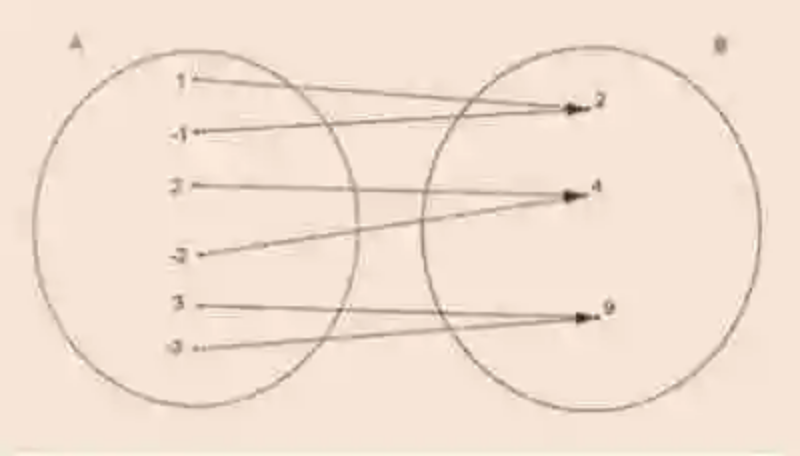
Además, la disciplina matemática señala que en la Correspondencia entre conjuntos también se pueden encontrar tres distintos tipos de colecciones, las cuales han sido explicadas de la siguiente manera:

• Conjunto inicial: también conocido como conjunto de partida, se entiende como la colección de elementos, desde la cual surge la correspondencia, así como las flechas que la indican. Por su parte, los elementos que hacen parte de la relación reciben el nombre de elementos antiimagen, al tiempo que tienen la responsabilidad de ejercer como el primer elemento del par de correspondencia. En el ejemplo usado para graficar esta relación, el conjunto inicial sería entonces el siguiente: A = {1, -1- 2, -2, 3, -3}
• Conjunto final: por otro lado, denominado igualmente como Conjunto de llegada, se encontrará esta otra colección, cuya principal característica es la de ser la colección en donde desemboca la relación de correspondencia, así también como las flechas que se encargan de señalarla. Con respecto a los elementos que hacen parte de este conjunto, las Matemáticas señalan que se denominarán como elementos imagen aquellos que sean partícipes en la correspondencia. En el ejemplo usado, el conjunto final sería este que se muestra a continuación: B = {2, 4, 9}
• Grafo: por último, en la Correspondencia entre conjuntos, existirá también la colección denominada tal como el criterio de relación: Grafo. En ella se podrán encontrar todos los pares de correspondencia que se han generado por medio de la relación. En el ejemplo citado el grafo sería el siguiente: G = {(1,2), (-1, 2), (2,4), (-2, 4), (3, 9), (-3, 9)}

Funciones

De igual forma, se llamará a capítulo el concepto de Funciones, las cuales han sido vistas como un tipo de correspondencia, la cual ocurre entre conjuntos siempre que todos los elementos relacionados que existen en el conjunto inicial cuenten con una sola imagen en el conjunto final. Un ejemplo de este tipo de correspondencia sería el siguiente:

En este tipo de correspondencia se encontrarán también dos distintos tipos de variables, las cuales han sido explicadas tal como se ve a continuación:

• Variable independiente: en primer lugar se encontrarán las variables independientes, que se distinguirán por ser denominadas por el nombre de x, y cuyos valores son aleatorios o independientes, es decir, que no se encuentran en función de ningún otro valor o variable.
• Variable dependiente: por otro lado, en las Funciones, también se encontrará la variable y, la cual es conocida como variable dependiente, y cuyo valor depende entonces tanto del valor de x como de la ecuación de la función, es decir, del conjunto de operaciones al que se somete el valor de x, según el criterio de correspondencia.

Dominio y Rango

Por último, también será necesario tomar un momento para revisar el concepto de Dominio y Rango, colecciones que hacen parte también de las Funciones matemáticas. No obstante, lo mejor será estudiar sus definiciones por separado:

• Dominio: de acuerdo a lo que señalan las Matemáticas, una Función es una relación entre conjuntos que ocurre toda vez que los elementos relacionados del conjunto inicial cuentan con una sola imagen en el conjunto final. Empero, esto no quiere decir que obligatoriamente todos los elementos del conjunto inicial se encuentren relacionados. Por ende, el Dominio de una Función podrá ser definido entonces como el conjunto de elementos del conjunto inicial que en este tipo de relación sí se encuentra vinculado.
• Rango: por igual, las Matemáticas señalan que el Rango de una Función será el conjunto de elementos del conjunto de llegada que sirven como imagen a los elementos del conjunto inicial.

Funciones de variable racional

Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre las Funciones de variable racional, las cuales han sido explicadas entonces como aquellas relaciones matemáticas, en donde los elementos pertenecientes al conjunto inicial, además de contar con una sola imagen, se caracterizan por estar conformados por números racionales, es decir, por elementos abstractos numéricos que pueden ser expresados como el cociente entre un número entero y un número natural positivo.

Por ende, las Matemáticas, también definen a las Funciones de variable racional como aquellas relaciones entre conjuntos en donde el Dominio se encuentra conformado por números racionales, que cuentan con una sola imagen en el Rango.

Imagen: pixabay.com