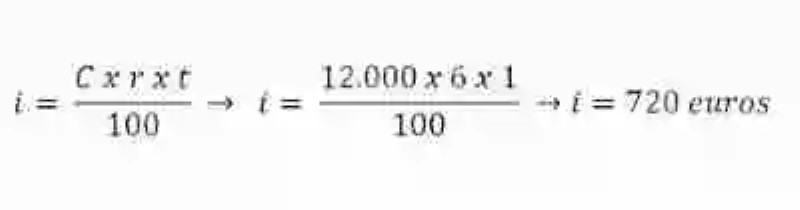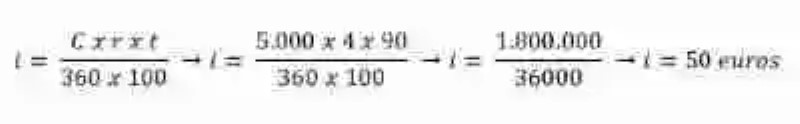Quizás lo mejor, antes de abordar una explicación sobre el Interés simple, sea revisar algunas definiciones, que de seguro permitirán entender este concepto dentro de su justo contexto matemático.
Definiciones fundamentales
En este sentido, puede que también sea de provecho delimitar esta revisión teórica a tres nociones específicas: Capital, Rédito y Tiempo, por ser las magnitudes entre las cuales se establece la proporción que dará como resultado el Interés simple. A continuación, una breve explicación de cada una de ellas:
Capital
De esta manera, se comenzará por decir entonces que el Capital ha sido definido de forma general, por las distintas fuentes matemáticas como el total de dinero que bien se consigna en una cuenta bancaria, o que por el contrario se da en préstamo a un tercero.
Tiempo
Por su parte, para determinar el Interés simple generado sobre un Capital específico, también se tomará en cuenta el Tiempo, el cual es definido entonces como el lapso que el dinero permanece consignado o en poder del beneficiario del préstamo.
Rédito
Finalmente, también será necesario tomar un momento para lanzar luces sobre el concepto de Rédito, el cual también es conocido como Tanto por ciento, y que básicamente puede ser explicado como la productividad que tienen cada 100 partes del dinero prestado o consignado (cada 100 dólares, cada 100 pesos, cada 100 euros) en el lapso de 1 año.
Interés simple
Una vez se han explicado cada una de estas magnitudes, puede que ciertamente sea mucho más sencillo aproximarse al concepto de Interés simple –conocido también como Interés a secas- y que es definido básicamente como la cantidad de dinero que produce en un tiempo determinado un capital específico, bien si esta se ha consignado en un banco, o si por el contrario se ha dado en préstamo.
No obstante, el Interés simple no depende únicamente del Capital que se ha prestado o del tiempo que este capital se ha entregado a la transacción, sino que se encuentra ligado directamente al rédito o tanto por ciento al cual se ha prestado. Por ende, de acuerdo a lo que señalan las distintas fuentes, el interés simple que puede obtenerse en un año sobre un capital que se ha prestado a un rédito específico, se determinará a través de una fórmula que lleva a multiplicar Capital por Tiempo y por Rédito, para luego este producto dividirlo entre 100, teniendo entonces la siguiente forma:
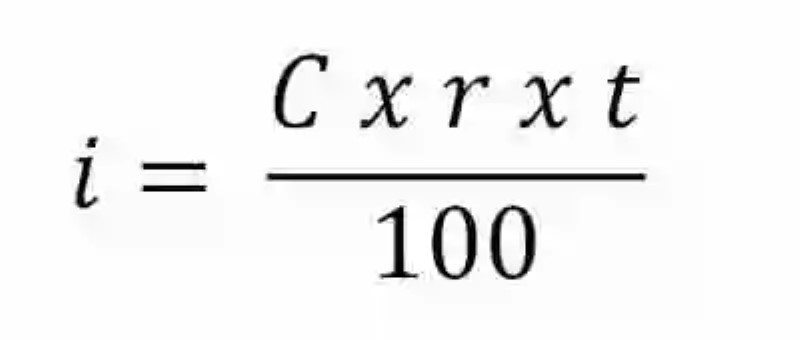
Sin embargo, también puede pasar que el tiempo no se encuentre expresado en años, sino en días. Para este tipo de casos, las Matemáticas señalan también otro tipo de fórmula, que llevará a multiplicar el Capital por el Rédito y por el tiempo, para finalmente dividir este producto entre el producto de 360 por 100, tal como puede verse a continuación:
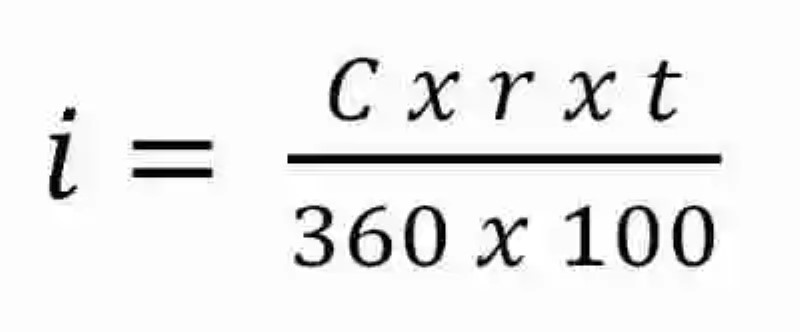
De igual forma, las Matemáticas señalan que el Interés simple es entonces directamente proporcional a cada una de las magnitudes que lo constituyen, puesto que si aumenta el Capital también aumentará el interés, así como si aumenta el Rédito o el Tiempo.
Ejemplos de interés simple
No obstante, puede que la mejor manera de completar una explicación sobre el Interés simple sea revisar la exposición de un ejemplo concreto, que permita entender la forma correcta en que deberá determinarse esta magnitud. A continuación, los siguientes ejemplos:
Ejemplo 1
Luis consignó en su cuenta de ahorros un total de 12.000 euros, ante la promesa de la institución de pagarle un rédito de 6 euros por cada 100. Si el tiempo que tendrá Luis esta cantidad a disposición del banco es de un año, ¿cuánto habrá ganado al cabo de este tiempo?
Una vez ha sido planteado el ejercicio, se deberá entonces exponer la información que se ha expuesto:
Capital: 12.000 euros
Rédito: 6 euros
Tiempo: 1 año
Interés: xCon estos datos, se deberá entonces completar la fórmula para determinar el interés simple:
El resultado obtenido será el interés simple que Luis ganará sobre el Capital que ha decidido depositar o consignar en su entidad bancaría. Para saber entonces cuánto dinero tendrá Luis al cabo de un año de haber hecho su consignación, bastará entonces con sumar el Capital que consignó Luis en primer momento más la ganancia que obtuvo al año:
12.000 + 720 = 12.720
Ejemplo 2
José Miguel le prestó a Paula un capital de 5.000 euros, a un rédito de 4%, y por un plazo de 90 días. Pasado este tiempo, ¿cuánto debe devolverle Paula a José Miguel si se suma el capital y la ganancia que le corresponde a este prestamista?
De igual forma, en este caso, lo primero que se debe hacer es plantear la información que ha presentado el ejercicio:
Capital: 5.000 euros
Rédito: 4
Tiempo: 90 días
Interés: xLo siguiente será entonces aplicar la fórmula de interés simple que se emplea cuando el tiempo se expresa en días:
Una vez se han determinado el interés simple, se deberá entonces sumar el capital prestado más esta magnitud determinada:
5.000 + 50 = 5.050 euros
Por ende, se ha podido encontrar entonces que luego de que José Miguel le ha prestado a Paula un total de 5.000 euros, a un rédito de 4%, esta muchacha deberá devolverle al cabo de 90 días un total de 5.050 euros, pues el interés simple es 50 euros.
Imagen: pixabay.com
El pensante.com (diciembre 24, 2018). Interés simple. Recuperado de https://elpensante.com/interes-simple/