Interpretación geométrica de la suma de números enteros

Definiciones fundamentales

En este sentido, puede que también sea conveniente delimitar esta revisión teórica a dos nociones específicas: la primera de ellas, la propia definición de Números enteros, por ser estos los elementos sobre los cuales se realiza la suma, y la posterior interpretación geométrica. Así también será necesario tomar un momento para pasar revista sobre el concepto de Recta numérica, por ser el gráfico sobre el cual se realiza la representación geométrica de la suma de número enteros. A continuación, cada una de estas definiciones:

Números enteros

De esta manera, se puede comenzar a decir que las Matemáticas han definido los Números enteros como aquellos elementos numéricos a través de los cuales se le da expresión escrita a cantidades exactas, o enteras, como su nombre lo señala. Igualmente, esta disciplina ha señalado los Números enteros como aquellos números que conforman el conjunto Z, y que se encuentran constituidos por tres distintos tipos de elementos:

• Números enteros positivos: estos números constituyen a su vez el conjunto de los Números naturales (N) por lo que entonces pueden ser empleados para contar los elementos de un conjunto, o incuso asignarles una posición o número específico, permitiendo ordenarlos. Se ubican en la Recta numérica, a la derecha del cero, desde donde se extienden en esa dirección al infinito. Son usados igualmente para indicar o expresar por escrito cantidades exactas o enteras. Poseen signo positivo, el cual sin embargo en ocasiones no se anota, dándose por sobreentendido.
• Números enteros negativos: por su parte, los números enteros negativos son interpretados como los inversos negativos de los enteros positivos. En consecuencia, se ubican en la Recta numérica a la izquierda del cero, punto desde donde se extienden –en sentido contrario a los positivos- hacia el infinito. Cuentan con signo negativo, el cual debe ser anotado en toda ocasión, para distinguirlo de su inverso positivo. Estos números son empleados para expresar por escrito la ausencia o falta de una cantidad específica.
• Cero: finalmente, el cero es considerado parte también del conjunto Z, o el conjunto de los Números enteros. Es ubicado en la Recta numérica en el centro, sirviendo de punto de origen tanto a números positivos como negativos. Sin embargo, el cero no es considerado un número como tal, sino un símbolo por medio del cual las Matemáticas logran dar expresión a la ausencia de cantidad plena. Por este motivo es que tampoco poseen signo, ni positivo ni negativo.

Recta numérica

En segunda instancia, será también necesario lanzar luces sobre la definición de Recta numérica, la cual ha sido entendida como un gráfico unidimensional –es decir, que solo representa una dimensión- sobre el cual se representan los números enteros. En este sentido, la Recta numérica también contará con la cualidad de ser graduada.

En el centro de ella, se ubicará el cero, y a partir de él, a espacios iguales, se colocarán los números enteros positivos,  hacia la derecha, y los de signo negativo hacia la izquierda. De esta manera, toda vez que se desee ubicar un número entero, de forma geométrica, se hará uso de la Recta numérica, por ser el gráfico matemático unidimensional que lo permite.

Interpretación geométrica de la suma de números enteros

Una vez se han revisado cada uno de estas definiciones, puede entonces que ciertamente sea mucho más sencillo abordar una explicación sobre el cómo debe realizarse toda interpretación geométrica de la suma ocurrida entre todo tipo de números enteros. En este orden de ideas, es necesario comenzar por recordar que la Suma puede ser definida como la operación matemática, por medio de la cual dos o más números específicos combinan sus valores, son el fin de obtener un total.

Así mismo, es necesario señalar que la Interpretación geométrica de esta operación sucedida entre números enteros ha sido explicada de forma general por las distintas fuentes matemáticas como el procedimiento por medio del cual se anota en la Recta numérica el significado o lo que realmente sucede a nivel matemático cuando se suman dos números enteros. Es decir, cómo la operación inicia en un punto específico de la Recta numérica, y según el número con el que sume, se avanzará hacia la izquierda o derecha de este gráfico, hacia el punto de destino, que representará el total de la operación.

No obstante, tomando en cuenta que los números enteros pueden ser tanto positivos como negativos, será necesario abordar cada uno de los casos específicos que se dan respecto a la suma de estos elementos, y el cómo debe hacerse su interpretación geométrica respectiva. A continuación, cada una de ellas:

Si se suman dos números enteros positivos

En caso de que los números involucrados en la suma fuesen positivos, entonces se asume que la operación de Suma realmente implica una adición. Así mismo, en cuanto a su interpretación geométrica en la Recta numérica, al estar la suma constituida por dos o más números enteros positivos, la representación de la operación deba ir hacia la derecha, por darse entre números positivos, así como por obtenerse un número positivo como total.

A la hora de realizar el procedimiento de interpretación se deberá entonces ubicar en la Recta numérica el primer sumando. Luego de esto, se contarán tantas cifras como valor tenga el segundo sumando involucrado, cifras que implicarán un desplazamiento hacia la derecha, es decir, en sentido positivo. Al encontrar el punto, se marca sobre la Recta numérica, y con una flecha, se representa el desplazamiento que ha ocurrido en este gráfico.

No obstante, puede que la mejor forma de explicar cómo debe hacerse la Interpretación geométrica de la suma de dos números enteros positivos sea a través de un ejemplo específico, tal como el que puede verse a continuación:

Supongamos que se ha dado una suma ente 1 y 4 (1+4= 5)

El resultado de esta operación será +5. A la hora de interpretar geométricamente esta operación, se deberá entonces marcar en la Recta numérica el 1, contar 4 espacios hacia la derecha, por tratarse ambos sumandos de enteros positivos. Este desplazamiento, debe originar un punto sobre el +5, que es el total de la suma:

Si se suman números enteros de distintos signos

Por otro lado, también puede ocurrir que los números enteros en la suma cuenten con signos diferentes. En consecuencia, según señala la disciplina matemática estos números deberán restarse, y el resultado deberá tener el signo del sumando mayor. Por ende, es el signo del total obtenido entre estos números enteros el que revelará si el desplazamiento, desde el punto de partida dado por el primer sumando, debe darse hacia la derecha, si el total es positivo, o hacia la izquierda, si el total es negativo.

A continuación, un ejemplo concreto de cómo debe hacerse la interpretación geométrica de la suma de dos números enteros de diferentes signos.

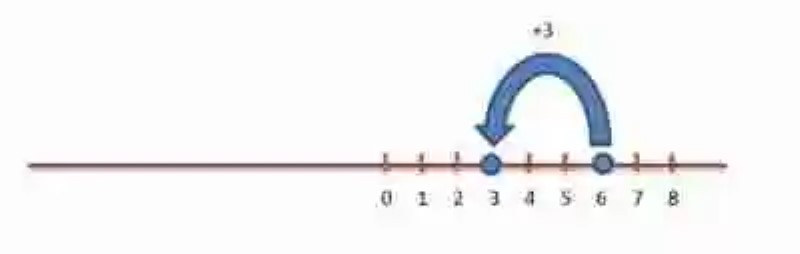
Suponiendo que la suma se haya dado entre -3  y + 6:    -3 +6 = 3

Entonces se deberá ubicar en la recta numérica el 6, y luego hacer un desplazamiento hasta el 3, el cual implicará un movimiento hacia la izquierda, pero dentro del segmento de la Recta numérica destinada para los números positivos:

Empero, también se puede dar el caso de que el número entero de signo negativo sea el que se establezca como el sumando mayor, por lo tanto el total obtenido será un número negativo, lo que implicará un desplazamiento hacia la izquierda.

Sin embargo, el punto de origen deberá ser tomado también en consideración, puesto que si el primer sumando es un número positivo, así el desplazamiento sea hacia la izquierda, y termine en el segmento de la Recta numérica destinado para los números negativos, entonces este movimiento empezará en realidad en el lado derecho de la Recta numérica. A continuación un ejemplo concreto de este tipo de casos:

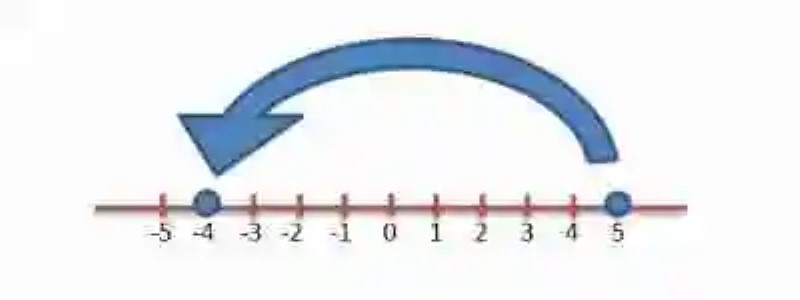
Si se tuviera que interpretar geométricamente la suma entre 5 + (-9)= cuyo resultado de la operación es -4, se deberá representar esta operación de la siguiente manera: Se comienza a partir del +5, en el lado derecho de la Recta numérica, y se hace un desplazamiento de 9 espacios hacia la izquierda, el cual debería concluir en -4:

Si se suman números enteros negativos

Finalmente, también puede suceder que los números enteros involucrados en la suma sean ambos negativos. En este caso, por contar con igual signo, simplemente se resolverá la adición, y al número obtenido se le asignará el signo negativo. Al momento de hacer su respectiva interpretación geométrica en la Recta numérica, esta deberá realizarse entonces en el segmento dispuesto para los números negativos. Se marcará el punto de inicio, el cual será dado por el primer sumando, mientras que el desplazamiento se hará hacia la izquierda, terminando en el punto asignado al total que se ha obtenido. Un ejemplo de esto será el siguiente:

Si se debiera realizar una operación de suma entre (-5) + (-4) =

Se resolverá entonces la operación:

(-5) + (-4) =

-5 -4 = -9

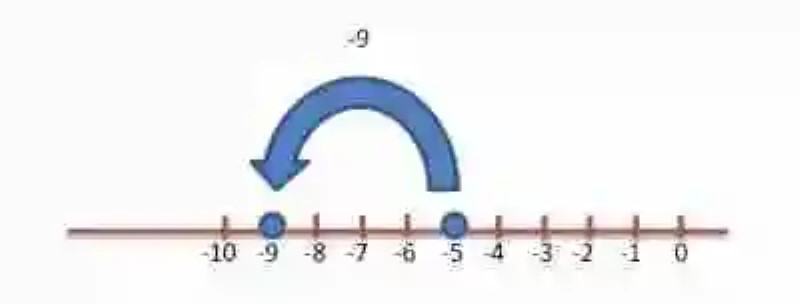
Y luego se procederá a interpretar geométricamente este resultado en la Recta numérica. Para esto, se anotara el punto de partida -5, y se marcará un desplazamiento hacia la izquierda de 4 puestos, el cual debería dar como resultado el -9:

Imagen: pixabay.com