Intervalos abiertos (funciones matemáticas)

Los conjuntos

De esta manera, se comenzará por decir que los Conjuntos han sido explicados por las Matemáticas como una clase de objeto, que se encuentra constituido por la reunión o agrupación de elementos, que se distinguen a la vez por contar con la misma naturaleza, de ahí que algunos autores prefieran definir los Conjuntos como colecciones abstractas de elementos homogéneos.

Así mismo, los Conjuntos cuentan con la característica de estar constituidos por una serie de elementos, que tienen la capacidad de determinarlos de una forma única y exclusiva. Por su parte, las Matemáticas han señalado también la manera correcta en que debe expresarse un conjunto: por un lado, la colección será denominada por medio de una letra mayúscula, mientras que los elementos que la conforman se expresarán como una numeración, separados por comas e incluidos entre signos de llaves: { }

La correspondencia

En segunda instancia, también se lanzarán luces sobre el concepto de Correspondencia, el cual ha sido explicado por las Matemáticas como un tipo de relación que existe entre dos conjuntos, siempre que uno, algunos o todos los elementos de una de sus colecciones encuentran en uno, alguno o todos los elementos de la otra colección, un tipo de correspondencia específica, la cual viene dada por un criterio determinado. Un ejemplo de este tipo de relación será el siguiente:

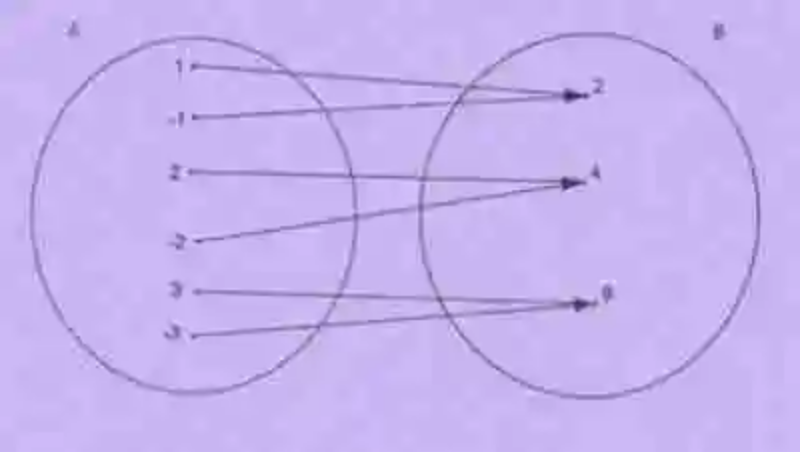
Además, las Matemáticas señalan que además de los dos conjuntos que participan de la Correspondencia, esta relación genera tres conjuntos adicionales, los cuales han sido explicados de la siguiente manera:

• Conjunto de inicio: conocido igualmente como Conjunto de partida o Conjunto inicial. Es descrito como la colección de la cual parte la correspondencia, así también como las distintas flechas que parten de ella. En cuanto a sus elementos, estos participan de la relación de correspondencia, recibiendo el nombre de antiimagen. Así mismo, estos elementos ejercerán como el primer término del par de correspondencia.
• Conjunto de llegada: denominado también como Conjunto final. Esta colección es señalada como el conjunto en el cual desemboca la relación de correspondencia, así como las flechas que son utilizadas para señalarlas. En cuanto a sus elementos, se encuentra conformado por los elementos que sirven de imagen a los del conjunto de inicio. Estos elementos cuentan con la responsabilidad de ejercer como segundo término del par de correspondencia.
• Grafo: así mismo, en esta relación matemática surgirá el Grafo, el cual es entendido como el conjunto que se forma por la reunión de todos los pares de correspondencia que se establecen entre los elementos del conjunto de inicio y los del conjunto de llegada.

Función

Otro de los conceptos sobre los cuales se pasará revista es la Función, la cual ha sido explicada como la relación matemática de correspondencia, que existe entre dos conjuntos, siempre que los elementos que participan de la relación y que pertenecen al conjunto de inicio encuentran en el conjunto de llegada una sola imagen para cada uno de ellos. Un ejemplo de este tipo de relación será el siguiente:

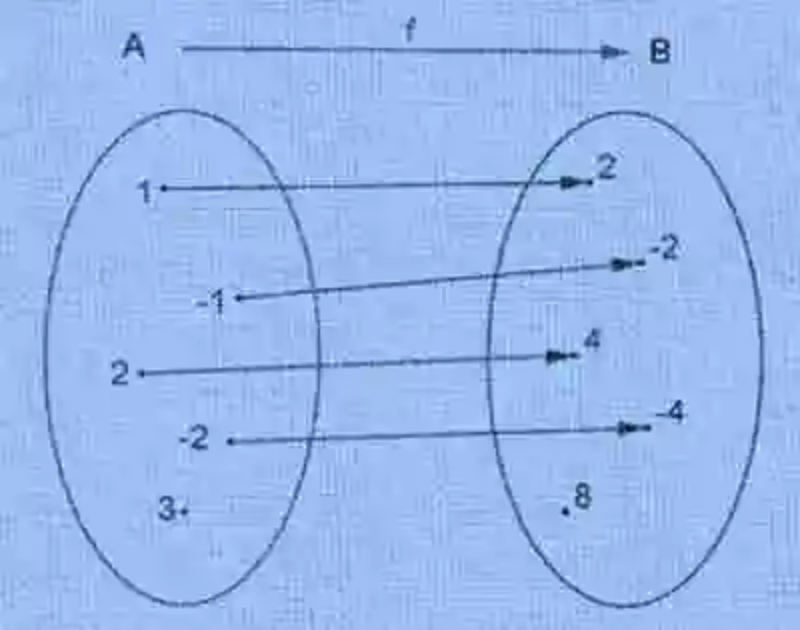
Variables de la función

Por igual, las Matemáticas han indicado que en la Función podrá hablarse de dos distintos tipos de variables, las cuales cuentan con la siguiente definición:

• Variable independiente: en primer lugar, se encontrará la variable independiente, la cual recibe también el nombre de variable x. Esta variable se distingue por contar con un valor que no depende de otra variable o término. En el par de correspondencia o de coordenadas ejerce como el primer término. Su tarea es someterse a la ecuación de la función, con el fin de determinar la variable y.
• Variable dependiente: por otro lado, en la Función también existirá la variable dependiente, o variable y, la cual ha sido explicada como la variable cuyo valor se encuentra completamente en función del valor de x, es decir, que depende de él. Su valor es determinado a través de la ecuación de la función, conjunto de operaciones matemáticas, que dependen a su vez del criterio de correspondencia.

Dominio y rango de la función

De igual forma, será necesario traer a capítulo el concepto de Dominio y rango de la función, los cuales han sido explicados de forma general como atributos específicos de las variables de este tipo de relación de correspondencia. Sin embargo, lo mejor será explicar brevemente cada uno de estos conceptos, tal como se muestra a continuación:

• Dominio: en primer lugar, se encontrará el Dominio, el cual ha sido explicado como el conjunto conformado por los posibles valores que puede asumir la variable x. En este punto es importante destacar que no siempre x puede asumir cualquier valor, por lo que el Dominio se encuentra supeditado a las posibilidades de la variable, impuestas por la ecuación de la función. Un ejemplo de esto puede ser el siguiente:

Suponiendo que se tuviese la función de forma y = √x

Se entendería que x no cuenta con la capacidad de asumir en esta función ningún valor negativo, en tanto que no existen raíces cuadradas de radicando negativo. Por ende, las Matemáticas reiteran que el Dominio sólo estará conformado por los valores que x está en capacidad de asumir.

• Rango: por su parte, el Rango de la función ha sido explicado por las Matemáticas como el conjunto que se encuentra conformado por los valores que asume la variable y, toda vez que los distintos valores de x han sido sometidos a las operaciones planteadas por la ecuación de la función.

Intervalos

Por último, también será necesario tener en cuenta el concepto de Intervalos, los cuales han sido explicados como el conjunto de valores reales que existen entre dos números específico. Para poder explicar este concepto en el ámbito de la función, se podría decir que el Intervalo se entiende como el conjunto de valores reales, que existen entre dos números, y que hacen referencia al Dominio que puede tener dicha función.

Para colocar un ejemplo de intervalo, se puede suponer que se tiene una función de forma:

y= √3-x

En este caso, se infiere que x no puede asumir nunca un valor mayor a 3, puesto que daría como resultado un radicando negativo e imposible. Por ende, se asume que los posibles valores para x son 0, 1, 2 y 3. Este grupo de números constituye el Dominio de la función, el cual podrá ser expresado como un intervalo.

Intervalo abierto

Una vez se han tomado en cuenta cada una de estas definiciones,  puede que ciertamente sea mucho más sencillo abordar una explicación sobre el Intervalo abierto, el cual es entendido como el conjunto de elementos, que se encuentra comprendido entre dos números específicos, que sin embargo no participan, es decir, que no son considerados como posibles valores para x.

En cuanto a la forma de expresión de esta clase de intervalo, las Matemáticas han señalado que este debe ser escrito como un par, constituido por los números que sirven de límite, aun cuando no son tomados en cuenta como valores para x, siendo además incluidos entre signos de paréntesis:

 (a, b)

No obstante, las Matemáticas también señalan que los intervalos abiertos pueden ser expresados por medio de signos mayor y menor que, los cuales señalarán cómo siempre x tendrá un valor mayor, pero no igual que el primer término, así como un valor menor, y no igual que el segundo término:

a < x < b

Otra de las formas admitidas por las Matemáticas para expresar este tipo de intervalos será el uso de corchetes invertidos, lo cuales encerrarán al par:

a,b[

Imagen: pixabay.com