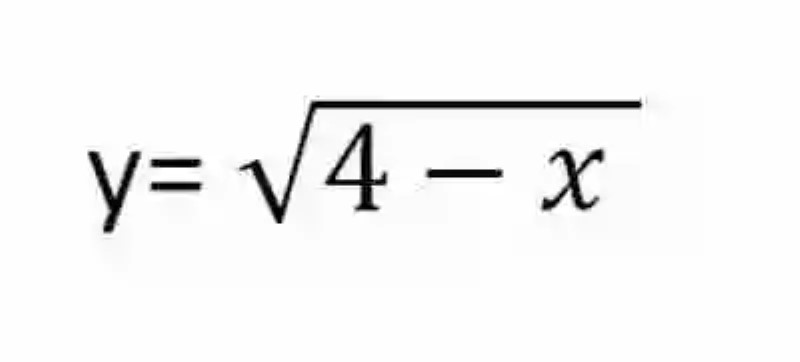Intervalos cerrados (funciones matemáticas)

Definiciones fundamentales

Por consiguiente, se tomará la decisión de delimitar esta revisión teórica a seis nociones específicas: Conjuntos, Correspondencia, Función, Variables de una función, Dominio y Rango de la función e Intervalos, por encontrarse directamente relacionados con el tipo de intervalos que se estudiará posteriormente. A continuación, cada uno de ellos:

Los conjuntos

De esta manera, se comenzará por revisar de forma breve la definición de Conjuntos, los cuales han sido explicados como un tipo de objeto matemático, constituido por un grupo de elementos, que se caracterizan por contar con la misma naturaleza. Así mismo, algunos autores han explicado los Conjuntos como un tipo de colección abstracta de elementos homogéneos.

Otra de las características que pueden encontrarse en los Conjuntos es la de tener elementos que cuentan con la capacidad de delimitarlos de forma única y exclusiva. En cuanto a la forma en que deben expresarse este tipo de objetos, la disciplina matemática señala que siempre deberán ser denominado por medio de una letra mayúscula, mientras que sus elementos se mostrarán como una enumeración, separándose por medio de comas, y encerrados entre llaves.

La correspondencia

Por otro lado, también será necesario tomar un momento para revisar el concepto de Correspondencia, la cual ha sido explicada por las diferentes fuentes como un tipo de relación matemática que existe entre dos conjuntos, cuando uno, alguno o todos los elementos de uno de ellos, según un criterio específico aplicado, encuentran correspondencia en uno, alguno o todos los elementos de la segunda colección. Un ejemplo de este tipo de relación será el siguiente:

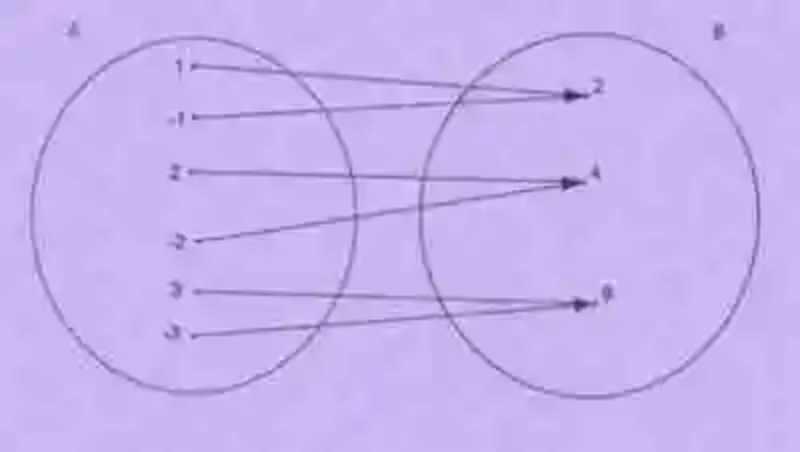
Así mismo, en la Correspondencia, además de los dos conjuntos entre los que se establece la relación, surgirán tres tipos distintos de colecciones, las cuales han sido explicadas de la siguiente manera:

• Conjunto de inicio: conocido también como Conjunto de partida o Conjunto inicial, esta colección se caracteriza por ser el objeto del cual parte la correspondencia, al igual que los signos de flecha empleados en señalarla. Por igual, estará conformado por los elementos que participan de la correspondencia, y que reciben el nombre de antiimagen. Este tipo de elemento funge como el primer término en el par de correspondencia.
• Conjunto de llegada: por otro lado, las Matemáticas señalan que otro de los conjuntos generados en la relación de Correspondencia es el Conjunto de llegada, o también el Conjunto final, descrito como la colección en la que desemboca la relación, así como las flechas que la señalan. Así mismo, este conjunto estará conformado por los elementos que participan de la correspondencia, y que recibirán el nombre de imagen, al tiempo que ejercen como segundo elemento del par de correspondencia.
• Grafo: en último lugar, se encontrará también el Grafo, el cual es entendido como un conjunto de elementos que se forma con la reunión de los distintos pares de correspondencia que se establecen en la relación.

Función

Así también, se lanzarán luces sobre el concepto de Función, la cual ha sido descrita a su vez como un tipo de correspondencia, que sucede siempre que uno, alguno o todos los elementos del conjunto de inicio encuentran una sola imagen en el conjunto de llegada. Un ejemplo de este tipo de correspondencia o aplicación será el siguiente:

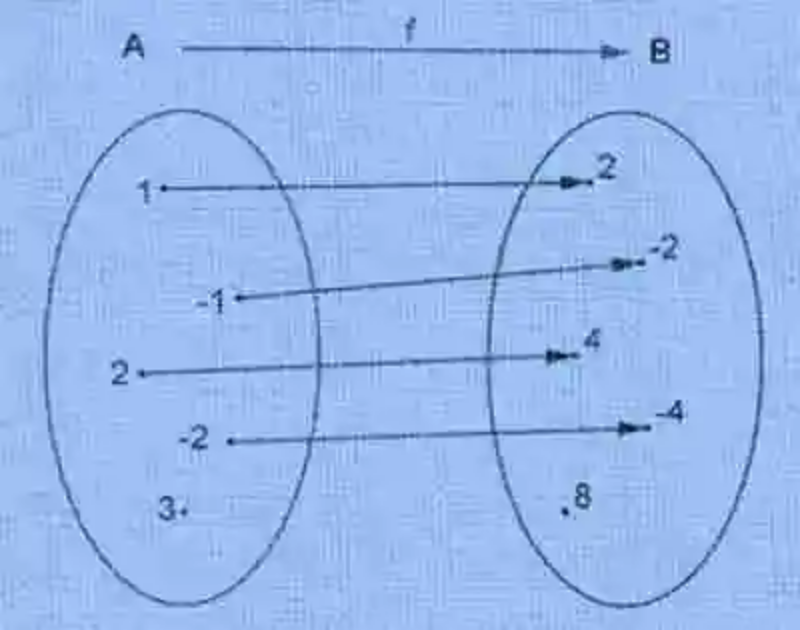
Variables de la función

De igual manera, las Matemáticas señalan que en la Función pueden existir dos diferentes tipos de variables, las cuales han sido explicadas de la siguiente manera:

• Variable independiente: también conocida como variable x, se caracteriza por contar con un valor que no depende de otras variables o términos. La función de esta variable es participar de la ecuación de la función, a fin de determinar el valor de y. En el par de correspondencia, o de coordenadas ejerce como primer término.
• Variable dependiente: conocida por su parte como variable y, esta variable tiene un valor que depende directamente –o se encuentra en función de- la variable x. Funge como segundo término en el par de correspondencia o de coordenadas.

Dominio y rango de una función

Entre los distintos atributos que pueden tener las variables de una función se encuentran el Dominio y el Rango, cada uno de los cuales han sido descritos de la siguiente manera:

• Dominio: en primer lugar se encontrará el Dominio, el cual podrá ser descrito como el conjunto que se encuentra conformado por todos los posibles valores que puede asumir x. En este sentido, es necesario colocar énfasis en la posibilidad, es decir, que x, en algunas funciones no puede asumir todos los valores, sino que sólo puede asumir algunos. Por ejemplo, si la ecuación de la función fuese la siguiente:

y = √x

Se entendería que x no podría asumir ningún valor negativo, en tanto que no existen respuestas para una raíz cuadrada de radicando negativo. Por ende, se asume que el Dominio solo lo conforman aquellos valores posibles para esta variable.

• Rango: por otro lado, también se encontrará el Rango, el cual ha sido explicado como el conjunto que se encuentra conformado por los distintos valores que asume y, siempre que x se somete a la ecuación de la función.

Intervalos

En consecuencia, si se piensa que la variable x no puede en todos los casos asumir todos los valores, se entiende que estos en algunas ocasiones serán limitados, es decir, estarán comprendidos entre ciertos valores. A este grupo de valores que puede tener x o el Dominio de una función, en un caso específico, se le conoce como intervalo.

Por ejemplo, si se tuviese la siguiente función

Se entendería que el valor de x no puede ser mayor de cinco, porque originaría un radicando negativo. Por ende, se asume que x sólo puede contar con los valores 0, 1, 2, 3 y 4. Ese sería el intervalo del Dominio de la expresión, el cual deberá ser expresado según el tipo de intervalo que constituye.

Intervalo cerrado

Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse al concepto de Intervalo cerrado, el cual básicamente se puede asumir como el conjunto de posibles valores para x, en donde se toman en cuenta también los límites de este conjunto. Es decir, que los elementos que sirven de referencia o límite para este conjunto sí se toman en cuenta.

Con respecto a la expresión de este tipo de intervalos, las Matemáticas señalan que este puede ser expresado como un par, conformado por el elemento inicial y el final, los cuales estarán encerrados entre corchetes:

[a, b

Sin embargo, este tipo de intervalo también puede ser expresado a través de signos menor o igual que o mayor o igual que, por medio de los cuales se mostrará cómo x siempre tendrá un valor mayor o igual al primer término que sirve de límite, al tiempo que será siempre menor o igual al término que sirve de segundo límite:

a≤ x ≤

Imagen: pixabay.com