
Antes de explicar la Media aritmética, así como la forma correcta de determinarla, se revisarán algunas definiciones, que permitirán entender entonces mucho más claramente la noción de esta medida de centralización.
Definiciones fundamentales
De esta manera, se tomará igualmente la decisión de delimitar esta revisión teórica a dos nociones específicas: Estadística y Medidas de centralización, por encontrarse directamente relacionadas a la medida de tendencia, que se estudiará posteriormente. A continuación, cada una de estas definiciones:
Estadística
En consecuencia, podrá comenzarse a decir que la Estadística puede ser entendida como una de las principales ramas de las Matemáticas, así como una de las distintas ciencias formales deductivas, definición que asume en tanto en la Estadística se puede encontrar la existencia de una teoría, así como la de un método científico formal, que la dota de la capacidad de hacer experimentos y observaciones, que no sólo resultan útiles a otras materias, sino que le sirven a ella misma para nutrirse.
De forma mucho más específica, la Estadística también ha sido explicada entonces como la ciencia formal que tiene como objetivo estudiar la variabilidad, probabilidad y frecuencia que puede tener un fenómeno determinado, en una población en específico.
Por consiguiente, no resulta extraño que las distintas disciplinas y ciencias formales hagan uso del método estadístico, para la realización de sus propios experimentos y observaciones, puesto que esta Ciencia cuenta con las herramientas suficientes para extraer los resultados y realizar las inferencias pertinentes que ayuden a conocer y predecir determinados fenómenos.
No obstante, aun cuando la Estadística es una sola materia, en realidad, dentro de ella se conciben dos distintas ramas, las cuales han sido explicadas de la siguiente manera:
- Estadística descriptiva: en primer lugar, se encuentra esta rama de la Estadística, la cual se encarga entonces de visualizar y describir de una forma bastante resumida los distintos datos, que han podido extraerse de un estudio. Por lo general, la Estadística descriptiva se vale de cuadros y gráficos para poder expresar las conclusiones que ha obtenido en base a sus experimentos y observaciones.
- Estadística inferencial: en segundo lugar, dentro de la Estadística, se habla de la rama de la Estadística inferencial, la cual se encarga entonces de estudiar los resultados que se han obtenido en base al estudio hecho sobre la muestra de una población, para luego hacer un proceso de inferencia estadística, que permita extrapolar el comportamiento de la muestra a toda la población, y así realizar entonces proyecciones sobre un fenómeno específico. En esta área se encuentran dos subtipos: la Estadística paramétrica y la Estadística no paramétrica.
Medidas de centralización
Así también, será necesario revisar el concepto de Medidas de centralización, las cuales han sido explicadas como aquellos parámetros centrales o valores intermedios, que pueden encontrarse ubicados en el centro de la distribución de datos, que se ha realizado en el estudio. Estas medidas también son conocidas como parámetros de tendencia central, parámetros centrales o tendencia central.
Dentro de los distintos tipos de Medidas de centralización, o parámetros centrales, se encuentran la Media aritmética, la Media ponderada, la Media geométrica, la Media armónica, la Mediana y la Moda. Cada una de estas medidas de centralización cuenta con su propio concepto y fórmula de determinación.
La media aritmética
Toda vez que se ha realizado esta revisión teórica, puede que ciertamente sea mucho más sencillo abordar una explicación sobre la Media aritmética, la cual ha sido explicada, de forma general, como una de las principales medidas de centralización, que pueden encontrarse en un estudio estadístico.
Desde una perspectiva mucho más específica, la Media aritmética, también conocida como media o promedio, ha sido explicada como el valor característico, correspondiente a una serie de datos cuantitativos, que se extraen entonces de un conjunto infinito de números o valores.
Según señala la disciplina estadística, la Media aritmética o Promedio se determina sumando todos los valores cuantitativos del conjunto de valores propios del conjunto que se estudia, y luego dividiendo el total entre el número de elementos que se han sumado para obtenerlo.
Así también, la Estadística concibe que la fórmula para obtener la Media aritmética:
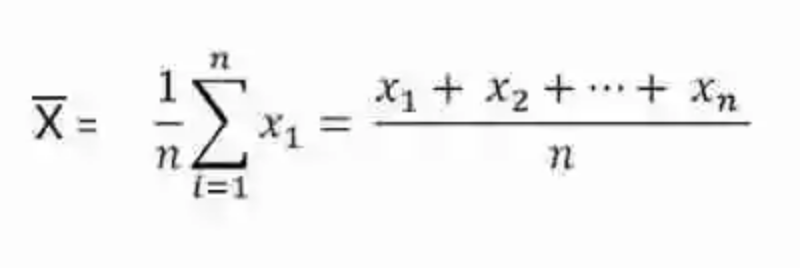
El pensante.com (diciembre 25, 2019). La media aritmética (Estadística). Recuperado de https://elpensante.com/la-media-aritmetica-estadistica/