Las medianas de un triángulo

Definiciones fundamentales

En este sentido, puede que también resulte de provecho delimitar esta explicación a cinco nociones específicas: la primera de ellas, la propia definición de Geometría, pues esto permitirá entender más claramente la naturaleza de la disciplina en medio de la que nace el concepto de Medianas de triángulo. Por igual, será necesario revisar los conceptos de Recta, Segmentos, Polígono y Triángulo, por encontrarse totalmente relacionada con las entidades que se revisarán posteriormente:

Geometría

Por consiguiente, se comenzará por decir que la Geometría ha sido explicada por la mayoría de los autores como una de las principales disciplinas de las Matemáticas. Así también, puede ser concebida como la materia que se encarga del estudio de las diferentes figuras, al igual que de cada una de sus distintas propiedades (volumen, área, altura, longitud). En consecuencia, algunas fuentes también señalan o ven a la Geometría como la Ciencia de las medidas.

Con respecto a su origen, existen teorías que señalan la Geometría como una de las disciplinas más antiguas de las Matemáticas. En este orden de ideas, hay fuentes que señalan que así como el concepto actual de Número natural pudo haber surgido de la noción de cantidad, manejada por el hombre primitivo en sus primeros intentos por administrar sus recursos, la noción de Geometría pudo desarrollarse igualmente en esta remota época, cuando los primeros hombres trataban de entender, medir, replicar y manipular las distintas formas de su entorno, como un esfuerzo para generarse mejores y más eficientes herramientas y espacios, elementos estos cruciales para una mayor posibilidad de sobrevivencia.

Recta

En segunda instancia, será necesario igualmente revisar el concepto que da la Geometría sobre la Recta, la cual ha sido explicada entonces como una figura geométrica unidimensional, constituida además por una sucesión infinita de puntos, elementos que deberán contar necesariamente con la misma dirección. Sin embargo, esto no hará que la Recta deba tener una sola posible dirección, pues en realidad esta figura geométrica tendrá dos distintos sentidos, los cuales dependerán básicamente de la lectura que se realice de esta figura geométrica. No obstante, estos no son los únicos rasgos que poseerá la Recta, la cual se caracterizará igualmente por contar con los siguientes rasgos:

• La Recta será entonces vista también como una figura geométrica infinita, pues al ser producto de una sucesión infinita de puntos, la Recta no tendrá ni principio ni final.
• Por otro lado, la Recta será entendida como la distancia más corta que existe entre dos puntos.
• Además, la Recta será la única figura geométrica que puede pasar a través de dos puntos, al tiempo que la Geometría señala que solo puede pasar una recta por oportunidad.
• Finalmente, la Recta será representada por una letra minúscula.

Segmento de recta

Otro concepto que será de utilidad en esta revisión teórica será el de Segmento de recta, el cual se entenderá entonces como la parte o sesión de la Línea recta, que surge en ella, toda vez que se ha trazado sobre esta figura geométrica unidimensional dos puntos. En consecuencia, el Segmento de recta contará con las siguientes características:

• Proviene de la Recta.
• Se encuentra delimitado por dos puntos.
• Al estar delimitado por dos puntos, el Segmento se diferencia de la Recta por ser finito, teniendo entonces tanto un punto de inicio como un punto de final.
• El segmento se representará siempre con una letra mayúscula.

Polígono

En cuanto a la definición de Polígono, este será entendido como una figura geométrica plana y bidimensional, es decir que contará solo con dos dimensiones: alto y ancho, sin que en ella pueda verse la tercera dimensión de la profundidad.

Además, la Geometría señala que el Polígono también podrá definirse como la figura geométrica que se encuentra totalmente delimitada por un conjunto de segmentos de recta. De hecho, esta condición produce uno de los rasgos más distintivos del polígono: contar con todos y cada uno de sus lados rectos, al punto de que si existiera alguna figura geométrica plana y cerrada, pero que tuviese uno solo de sus lados curvos, entonces no podría ser considerado un polígono como tal. Por otro lado, el Polígono también se distinguirá por ser una figura geométrica constituida por cuatro elementos específicos:

• Lados: en primer lugar, los lados, los cuales estarán constituidos por segmentos de recta. Estos constituyen el propio polígono, al punto que cada una de estas figuras geométricas se denomina según el número de lados que posee.
• Vértice: al ser una figura cerrada, los lados de los polígonos se unen en un punto particular, en donde confluyen dos puntos, los cuales se denominan vértice. Estos pueden encontrarse de manera contigua o no.
• Ángulo: sin embargo, cuando dos lados se encuentran no solo se formará un vértice, sino que estos lados comenzarán a delimitar un espacio geométrico específico, el cual contará  a su vez con los siguientes elementos: dos lados, que servirán de límites y que estarán constituidos por los segmentos de recta del polígono; un vértice que coincide plenamente con el vértice del polígono; y una amplitud, la cual puede ser medida en grados sexagesimales.
• Diagonales: con respecto a las Diagonales, la Geometría señala que estas se pueden definir como aquellos segmentos de recta, que se extienden entre dos vértices, los cuales deben contar con la cualidad de ubicarse de forma no continua.

Triángulo

Por su lado, el Triángulo será entendido como el polígono o figura geométrica plana, es decir, bidimensional, que se encuentra completamente cerrada, es decir, delimitada por tres distintos segmentos de recta o lados rectos. Sin embargo, esta no es la única característica del Triángulo, pues este polígono se encontrará constituido también por los siguientes elementos:

• Tres lados: en primer lugar, los Triángulos contarán con tres lados. De hecho, es la igualdad o la diferencia entre cada uno de estos lados entre sí los que sirven a la Geometría como uno de los principales rasgos en base a los cuales se hace una clasificación de Triángulos, los cuales se dividirán entonces entre Triángulos equiláteros, Triángulos isósceles y Triángulos escalenos.
• Tres vértices: siendo el Triángulo un polígono, será una figura cerrada, por lo que sus lados coincidirán entre sí, creando puntos en común. En el caso del triángulo podrán contarse entonces tres vértices, los cuales se encontrarán situados siempre de forma contigua.
• Tres ángulos: así mismo, dentro de los Triángulos podrán encontrarse entonces tres ángulos, los cuales serán entendidos como los espacios geométricos, delimitados por dos lados del triángulo, y que cuenta con un vértice y una amplitud, medida en grados sexagesimales. En cuanto a los triángulos, la Geometría señala que las distintas amplitudes que ellos presentan servirán también para establecer una clasificación de triángulos, separándolos entonces entre Triángulos acutángulos, Triángulos rectángulos y Triángulos obtusángulos.
• Sin diagonales: por último, uno de los rasgos de los triángulos es contar con tres vértices que se encuentran de manera contigua, por lo que no se puede decir que en ellos sea posible la existencia de diagonales.

Las medianas de los triángulos

Una vez se han revisado estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre las Medianas de los triángulos, entidades geométricas que serán entendidas como aquellos segmentos, que trazados dentro del triángulo, se encargan de extenderse entre un vértice y el punto medio del lado que se presenta opuesto al vértice del cual nace. Al tazarse todas las Medianas de un triángulo, estas tienden a cortarse en un punto en común, el cual recibirá el nombre de Baricentro.

Ejemplo de cómo trazar las Medianas de un triángulo

Empero, puede que lo más apropiado a la hora de explicar las Medianas de un triángulo, sea revisar de forma breve un ejemplo de cómo se trazan y deben lucir estos segmentos de recta, tal como se ven a continuación:

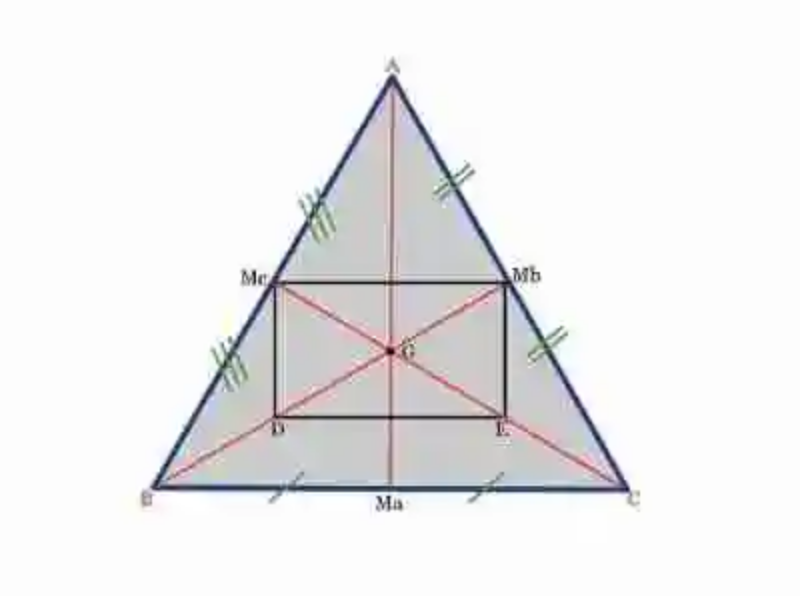
Dado el siguiente triángulo ABC, se deberá calcular cuál es el punto medio del lado CB, el cual se encuentra opuesto al vértice A. Al hacerlo, este punto deberá unirse, por medio de un segmento, con el vértice A, generando entonces un segmento AM.

Así mismo, se tomará el lado AC, y se determinará cuál es su punto medio, que se denominará por ejemplo punto P. Al hacerlo, se trazará entonces un segmento hasta el vértice B, generando el segmento PB.

Por último, se buscará el punto medio del lado AB, creando con esto el punto N. Se trazará entonces un segmento NC.

Estos tres segmentos pueden ser consideraos como las Medianas del triángulo: AM, PB y NC. Todos pasan por un punto en común, en donde estos segmentos se intersectan, generando entonces el punto G, el cual se denominará baricentro, el cual en ocasiones es también llamado centro de gravedad del triángulo, es decir, el punto en donde –en términos físicos- se encontrará el punto de aplicación del peso de esta figura geométrica, en caso de que se materializara, por ejemplo en un triángulo de cartón.

De hecho, una forma de comprobarlo es precisamente haciendo un triángulo de cartón, y apoyándolo sobre un alfiler, si realmente el punto es un baricentro, entonces la figura podrá mantenerse en total equilibrio pues este será el centro de gravedad o punto de aplicación de su peso.

Imagen: 1.- pixabay.com / 2.- wikipedia.org