Magnitudes directamente proporcionales

Definiciones fundamentales

En este sentido, puede que sea recomendable delimitar esta revisión a tres definiciones particulares: Razones, Proporciones y Cantidades de magnitudes, las cuales se encuentran directamente relacionadas con las Magnitudes directamente proporcionales. A continuación, cada uno de estos conceptos:

Razones

En primer lugar, se encuentran las Razones, las cuales han sido explicadas como aquellas expresiones que dan cuentan del cociente de dos números, los cuales pueden ser expresados de la siguiente manera:

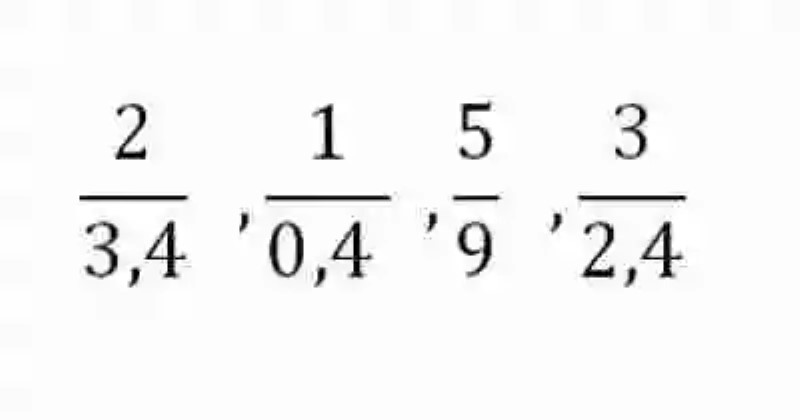
En este punto, es importante señalar la importancia de no confundir las Razones con las Fracciones. Al respecto, las distintas fuentes señalan que estas últimas –conformadas por el Numerador y el Denominador- dan cuenta de cuántas partes se han tomado de una unidad, que se encuentra dividida en partes, mientras que las Razones –constituidas por los Antecedentes y los Consecuentes- se usarán para expresar el cociente de dos números, es decir, la cantidad de veces que el Divisor se encuentra dentro del Dividendo.

Proporciones

Así también, será necesario central la atención en el concepto de Proporciones, las cuales han sido explicadas como la relación de igualdad que existe entre dos razones, cuando estas, independientemente de los valores de cada una de sus partes, conducen al mismo cociente, y ademán al multiplicar sus medios –es decir el consecuente de la primera por el antecedente de la segunda- y sus extremos –el ascendente de la primera por el antecedente de la segunda- se obtiene igual resultado.

Cantidades de Magnitudes

Finalmente, resultará pertinente revisar el concepto de Cantidades de Magnitudes. Sin embargo, para esto será necesario comenzar por la propia definición de Magnitudes, las cuales serán descritas como los conjuntos que se encuentran compuestos por elementos, que cuentan con la cualidad de poder sumarse, compararse u ordenarse. De acuerdo a lo que señalan las distintas fuentes, algunas propiedades de los segmentos, los recipientes o los cuerpos, como por ejemplo la longitud, la capacidad o la masa puede ser considerados como magnitudes.

Por su parte, las Matemáticas han señalado que las Cantidades de Magnitudes son los elementos que conforman las magnitudes, es decir, aquellos que pueden sumarse, compararse u ordenarse. Así mismo, las diferentes fuentes han indicado que las Cantidades de magnitud pueden medirse comparándose con otra, que necesariamente debe ser homogénea, y que es reconocida con el nombre de Unidad, siendo entonces señalada por medio de la letra “u” minúscula.

Magnitudes directamente proporcionales

Una vez se han revisado cada una de estas definiciones, quizás sea mucho más sencillo abordar el concepto de Magnitudes directamente proporcionales, las cuales han sido explicadas entonces como aquellos pares de magnitudes que cumplen con la propiedad de que cuando una de ellas se multiplican o dividen por o entre un número específico, inmediatamente la otra magnitud también se multiplica o divide entre este número.

De igual forma, las Matemáticas señalan que estas dos magnitudes pueden establecer también razones, cuya resolución arroja un cociente, que es denominado como Constante de proporcionalidad directa. Así mismo, en las Magnitudes directamente proporcionales se encuentran algunas leyes o propiedades, las cuales han sido explicadas de la siguiente manera:

• La razón de las dos cantidades de la primera magnitud resulta proporcional a la razón de las segundas magnitudes.
• Por igual, se tendrá que los valores de una magnitud resultan totalmente proporcionales a los valores de la otra magnitud, por lo que entonces se tiene que estas pueden crear series de razones iguales.

Imagen: pixabay.com