
Quizás lo mejor, antes de abordar una explicación de Magnitudes inversamente proporcionales, sea recomendable revisar algunas definiciones, que de seguro permitirán entender de forma contextualizada esta relación matemática.
Definiciones fundamentales
En este sentido, puede que también sea productivo delimitar esta revisión teórica a dos conceptos específicos: Razones y Proporciones, por encontrarse directamente relacionados con la noción de Magnitudes Inversamente Proporcionales. A continuación, cada uno de estos conceptos:
Razones
Por consiguiente, se comenzará por decir que las Razones han sido explicadas como las expresiones matemáticas, que dan cuenta del cociente que existe entre dos números, es decir, de la cantidad de veces que se encuentra incluido el Divisor dentro del Dividendo. Algunos ejemplos de Razones serán las siguientes:
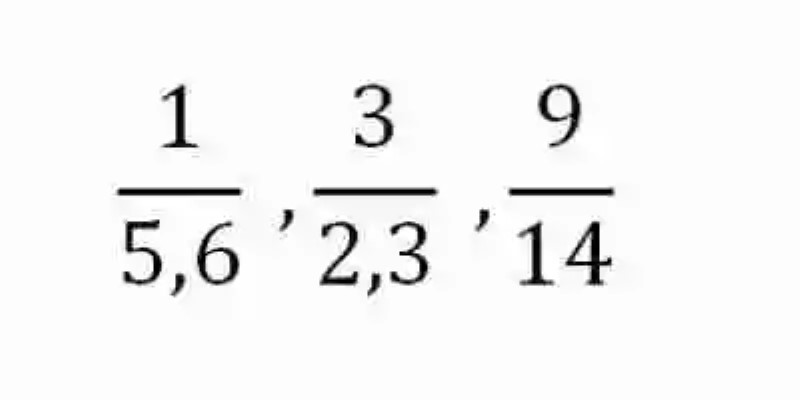
Según señalan las distintas fuentes, las Razones estarán conformadas por dos elementos: el Antecedente, el cual ocupará el ámbito superior de esta expresión, al tiempo que señala el Dividendo; y el Consecuente, elemento que pertenece al ámbito inferior, encargándose de señalar el Divisor de la división que conduce al Cociente, que expresa la Razón.
Así mismo, las Matemáticas señalan que pese al parecido que existe entre las Razones y Fracciones, estas expresiones no deben ser confundidas, puesto que cuentan con elementos diferentes, mientras que señalan realidades diferentes. De esta manera, se tendrá que las Razones –conformadas por el Antecedente y el Consecuente- señalan el cociente entre dos números, y las Fracciones, por su parte –constituidas por el Numerador y el Denominador- refiere a la cantidad de partes que se toma de una unidad, dividida en partes iguales.
Proporciones
En segunda instancia, será necesario también revisar la definición que han dado las Matemáticas sobre las Proporciones, las cuales han sido explicadas como la relación de igualdad que existe entre dos razones, es decir, las Proporciones son dos razones que resultan iguales entre ellas. A continuación, algunos ejemplos de este tipo de relaciones:

En este caso, se podrá ver cómo a pesar de tener todos sus elementos con distintos valores, estas razones serán consideradas proporcionales, puesto que si se resolvieran, en ambos caso se obtendría un cociente igual a 2. Por lo tanto, se consideran razones iguales, ya que expresan el mismo cociente.
Sin embargo, esta no es la única manera que conocen las Matemáticas para determinar si dos razones son o no proporcionales. Al respecto, las distintas fuentes han señalado que también se podrá recurrir al método de los extremos y los medios. Para esto, se deberá entonces multiplicar los extremos –constituidos por el Antecedente de la primera razón y el Consecuente de la segunda- y los medios –conformados por el Consecuente de la primera expresión y el Antecedente de la segunda razón. Si estas expresiones fuesen proporcionales, en ambas multiplicaciones se obtendría iguales productos:
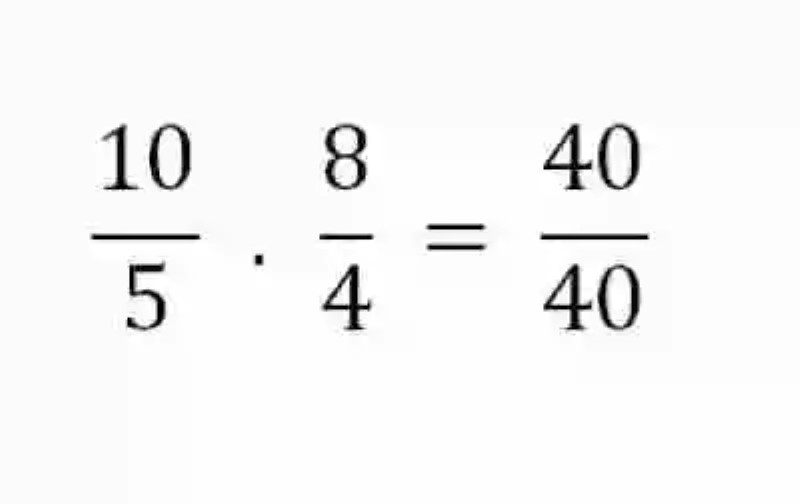
Este atributo es conocido como una de las leyes de la proporción, y resulta bastante útil a la hora de despejar o conocer algunos de los elementos de las razones proporcionales, que se presentara como incógnito, pues para esto se necesitaría simplemente realizar un procedimiento de Regla de Tres Simple Directa, en donde se multiplicarán entre sí los elementos del ámbito completo, para luego dividir este producto entre el único elemento del ámbito que desea complementarse:
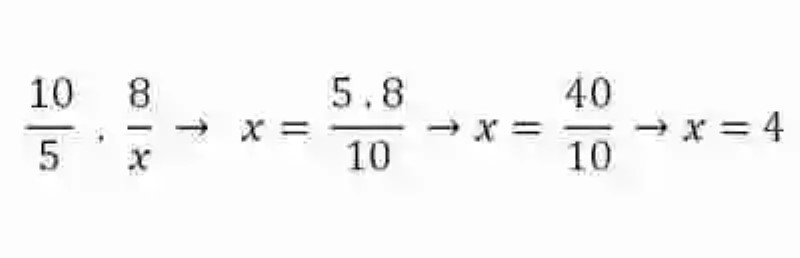
Magnitudes
Finalmente, será necesario también tomar un momento para tener en cuenta el concepto de Magnitudes, las cuales han sido explicadas como el conjunto de elementos, que cuentan con la capacidad de sumarse, ordenarse y compararse con otras homogéneas o semejantes.
Magnitudes inversamente proporcionales
Una vez se han revisado estas definiciones, puede que ciertamente sea mucho más sencillo tomar un momento para aproximarse al concepto de Magnitudes inversamente proporcionales, las cuales han sido explicadas como aquel conjunto de dos Magnitudes en donde si una se multiplica por un factor específico, la otra que constituye par con la primera, queda dividida por el mismo factor. Es decir, ambas magnitudes del par inversamente proporcional se ven afectados por el mismo factor, pero de manera inversa, pues mientras a una la multiplica, a la otra magnitud la divide.
Así mismo, las Matemáticas han señalado que en las Magnitudes inversamente proporcionales se pueden ver dos propiedades específicas:
1.- En primer lugar, cualquier razón establecida entre dos cantidades cualquiera que puedan observarse en la primera magnitud siempre establecerán proporción con la razón establecida entre cualquier par de cantidades de la segunda magnitud.
2.- Por otra parte, los valores de una magnitud –del par de magnitudes inversamente proporcionales- resultan directamente proporcionales a los inversos de los valores que se pueden encontrar en la otra magnitud. Esto quiere decir que si la primera magnitud se multiplica por dos, la otra magnitud se dividirá en su mitad.
Ejemplo de Magnitud inversamente proporcional
Empero, puede que la mejor manera de cerrar una explicación sobre las Magnitudes inversamente proporcionales sea revisar un ejemplo concreto, que permita ver cómo se establece esta relación matemática entre dos magnitudes. A continuación, el siguiente caso.
De acuerdo a lo que señalan las distintas fuentes la relación entre la velocidad en que un vehículo se desplaza por un espacio específico y el tiempo que tarda en hacerlo pueden constituir una magnitud inversamente proporcional, en tanto en que a mayor velocidad se desplaza el vehículo menor tiempo tomará para hacerlo.
Por ejemplo, si el vehículo se desplaza a 60 km/H para recorrer 360 kilómetros, se demorará 6 horas:
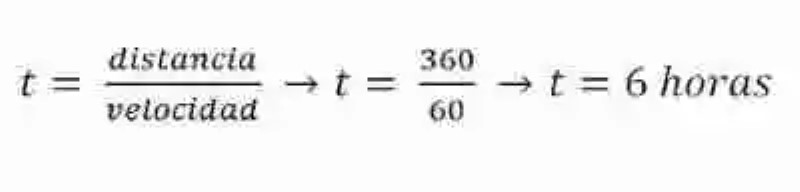
No obstante, si la velocidad aumentara, teniendo que recorrer el mismo espacio, por ejemplo a 80 km / h, este vehículo se demoraría en recorrer este espacio un total de 4,5 horas
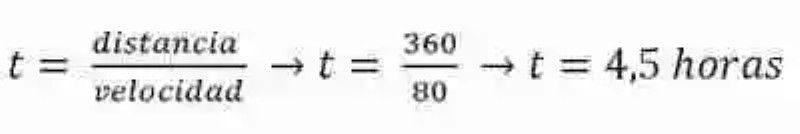
Por ende, se ve que a mayor velocidad menor tiempo en recorrer una distancia específica, por lo que entonces velocidad y tiempo pueden considerarse magnitudes inversamente proporcionales, pues mientras de una de ellas se multiplica por un factor, la otra se divide por el mismo, que en este caso sería la distancia.
imagen: pixabay.com
El pensante.com (noviembre 28, 2018). Magnitudes inversamente proporcionales. Recuperado de https://elpensante.com/magnitudes-inversamente-proporcionales/