Magnitudes proporcionales a otras varias

Definiciones fundamentales

De esta manera, se delimitará esta revisión a cuatro nociones específicas: Razones, Proporciones, Magnitudes y Magnitudes directamente proporcionales, por encontrarse relacionadas estrechamente con la relación que se estudiará posteriormente. A continuación, cada una de estas definiciones:

Razones

Por consiguiente, se tendrá que las Razones han sido explicadas por las Matemáticas como una expresión, que cumple con la misión de indicar el Cociente existente entre dos números. Es decir, que la Razón señala cuántas veces se encuentra incluido el Divisor dentro del Dividendo. Algunos ejemplos de razones pueden ser los siguientes:

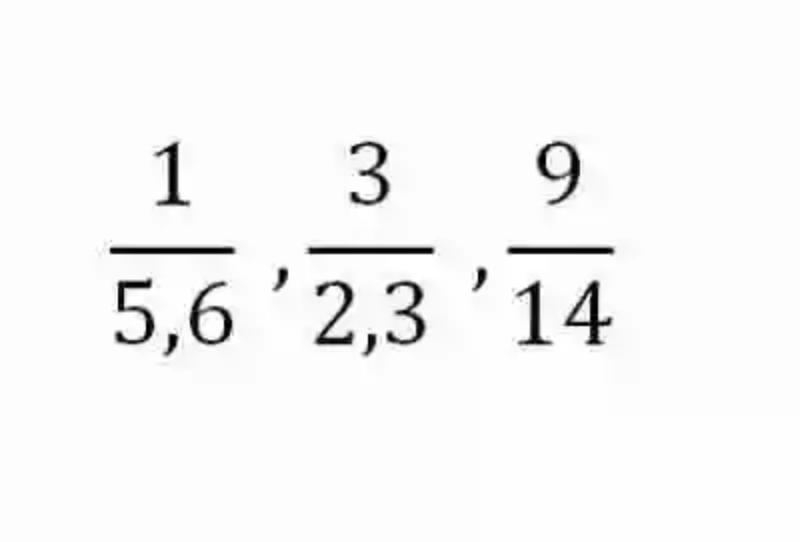
De acuerdo a lo que señalan los distintos autores, las Razones se encuentran conformadas por dos elementos: el primero de ellos, el Antecedente, el cual ocupa la parte superior de la razón, encargándose de señalar el Dividendo; y en segundo lugar, estará el Consecuente, elemento que ocupa el ámbito inferior de la razón, con el fin de señalar cuál es el Divisor.

Así mismo, las Matemáticas han referido la importancia de no confundir las Razones con las Fracciones, pues pese al parecido que tienen estas en cuanto a sus estructuras, en realidad se encuentran conformadas por elementos distintos, al tiempo que se constituyen como expresiones de distintas realidades matemáticas.

En este sentido, las Razones –constituidas por el Antecedente y el Consecuente- expresarán el Cociente entre dos números, mientras que las Fracciones –conformadas por el Numerador y el Denominador- darán cuenta de cuántas partes se han tomado, respecto a una unidad, dividida en partes iguales.

Proporciones

En segundo lugar, también será necesario revisar la definición de Proporciones, las cuales serán entendidas como la relación de igualdad que existe entre dos razones. Por ende, dos razones iguales son dos razones proporcionales. Algunos ejemplos de este tipo de relación será la siguiente:

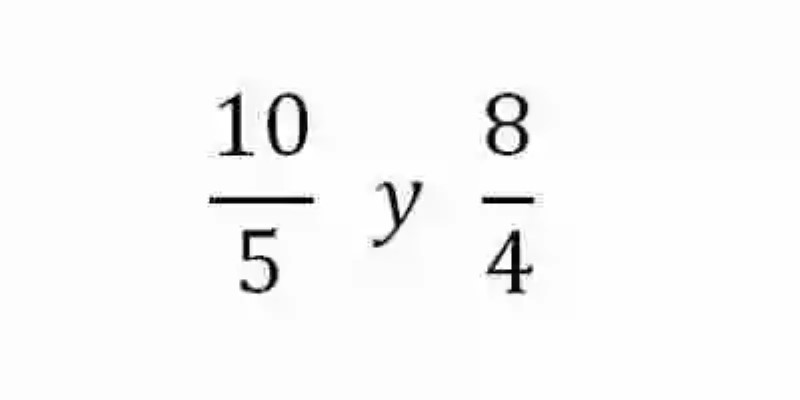
Al tener en cuenta este caso, se puede ver entonces cómo pese a que ninguno de los elementos de estas razones coinciden entre sí, estas podrán considerarse como iguales, en tanto que si se resolvieran ambas arrojarían un cociente igual a dos, es decir que estas razones se pueden considerar como expresiones del mismo cociente.

Sin embargo, este no es el único método que las Matemáticas conciben para determinas si dos razones son o no son proporcionales. De esta manera, esta disciplina señala que también puede emplearse con este propósito el método de los Extremos y los Medios. Por ende, se podrán multiplicar entre sí los Extremos –es decir, el Antecedente de la primera razón por el Consecuente de la segunda- y hacer lo mismo con los Medios –conformados por el Antecedente de la primera razón y el Consecuente de la segunda. Si las razones son proporcionales, ambas multiplicaciones arrojarán productos iguales:

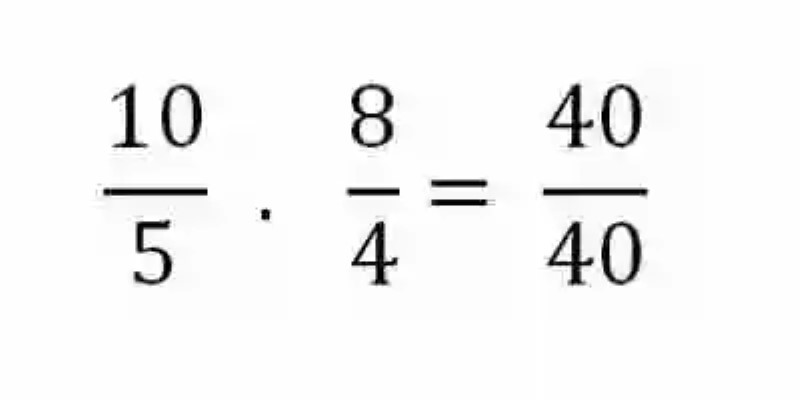
Este rasgo de las razones proporcionales, es conocido por lo general como una de las Leyes de la proporción, y resulta bastante útil toda vez que alguno de los elementos de las razones resulten desconocidos, puesto que para despejarlo, bastará con ejecutar una Regla de tres simple directa, multiplicando entonces los elementos del ámbito que se encuentra completo, bien si están conformados por los extremos o los medios, para después dividir este producto entre el único elemento que se conoce del ámbito que se desea completar:

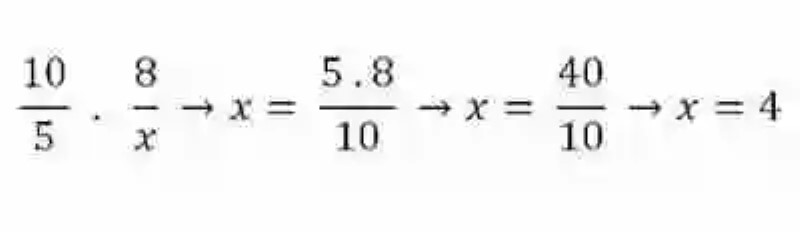
Magnitudes

En tercer lugar, será igualmente importante tomar un momento para tener en cuente el concepto de Magnitudes, las cuales han sido explicadas por los distintos autores como el conjunto de elementos, que cuentan con la cualidad de sumarse, compararse u ordenarse en base a unidades que les resulten en todo momento semejantes o iguales.

Magnitudes directamente proporcionales

Finalmente, antes de continuar con el concepto de Magnitud proporcional a otras varias, será necesario lanzar luces sobre el concepto de Magnitudes directamente proporcionales, las cuales han sido descritas por las Matemáticas como el par de Magnitudes, en donde puede verse la propiedad de que cuando una de ellas se multiplica o divide por un factor específico, la segunda reacciona de la misma forma, es decir, se multiplica o divide por el mismo factor.

Magnitud proporcional a otras varias

Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse a una explicación sobre la Magnitud proporcional a otras varias, las cuales han sido entendidas como uno de los tipos de proporciones que pueden existir entre Magnitudes, cuando una de ellas se encuentra fija, mientras que las otras dos con las que se relacionan, resultan directamente proporcionales entre sí. Es decir, que una Magnitud es proporcional a otras varias cuando ella permanece fija y las otras restantes establecen proporciones entre ellas.

Así mismo, debido a que en la Magnitud proporcional a otras varias no intervienen tan solo dos magnitudes, como ocurre por lo general en las Magnitudes directamente proporcionales, el objetivo entonces cuando se trabaja con el primer tipo de magnitudes es lograr expresar una proporción, construida en base todas las magnitudes que participan en la relación de esa Magnitud proporcional a otras varias. De esta manera, se podrán ver proporciones con más de dos magnitudes o razones.

Ejemplo de Magnitud proporcional a otras varias

Sin embargo, puede que lo mejor, a la hora de explicar este tipo de proporcionalidad entre magnitudes, sea a través de un ejemplo en concreto, que permita ver cómo se da en la práctica este concepto, tal como se puede ver a continuación:

Si se tuviera una carpintería en donde 6 carpinteros produjeran en 4 horas 10 sillas, se podría tener entonces, como señala el siguiente gráfico, que si se fijara la Magnitud de números de Carpinteros, se podrían entonces concebir las otras dos como Magnitudes directamente proporcionales, en tanto que si aumentaran el número de horas de trabajo también se vería un aumento en cuanto al número de sillas fabricadas. Por ejemplo, si el número de horas se multiplicara por 3, el número de sillas también lo haría, pero el número de carpinteros permanecería igual, porque es la magnitud que se ha fijado:

Al hacer esto, se obtiene entonces una proporción entre las razones creadas con las Magnitudes directamente proporcionales relacionadas con esta magnitud fijada:

Proporción resultante del número de carpinteros fijado en 6 :

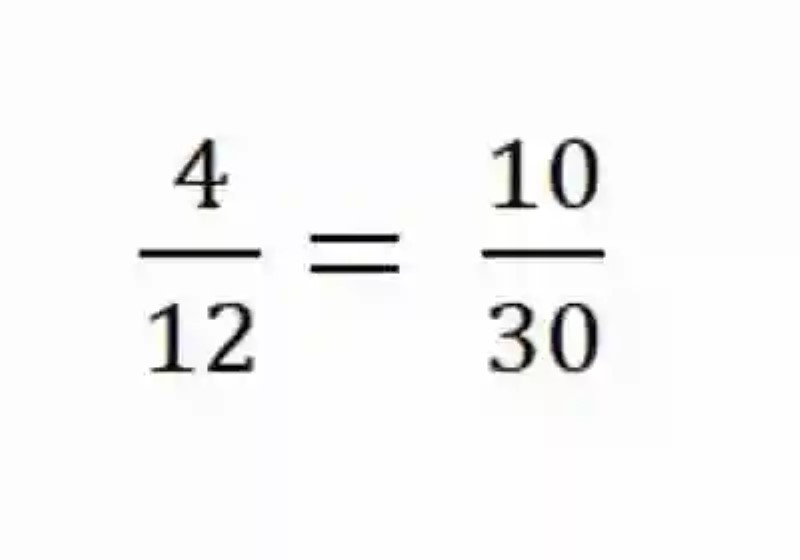
Por el contrario, si se quisiera fijar otra de las Magnitudes, como por ejemplo las horas de trabajo, se podría ver cómo el Número de carpinteros y el número de sillas podrían establecerse como Magnitudes directamente proporcionales, en donde si una aumenta o se multiplica por un factor, la otra responde de la misma manera, es decir, de forma directa y proporcional. Por ejemplo, si tanto el número de carpinteros como el número de sillas se multiplicara por tres, mientras que se mantiene el número de horas de trabajo fijadas en 4, se obtiene lo siguiente:

Esta realidad se puede fijar en la siguiente proporción:

Horas de trabajo fijadas en 4:

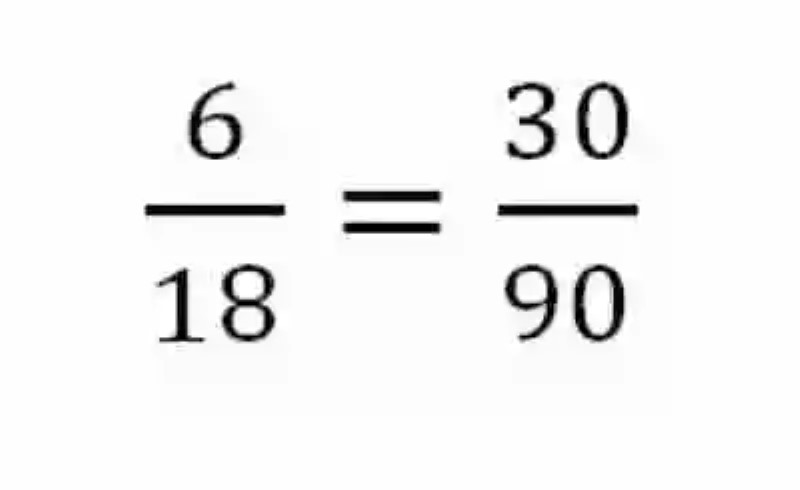
Así mismo, las Matemáticas señalan que pese a que las proporciones por lo general están conformadas por dos razones que resultan iguales, en tanto dan cuenta del mismo cociente, cuando se trata de Magnitudes proporcionales a otras varias, se puede lograr expresar una proporción en donde se puedan inscribir todas las proporciones existentes, e incluso una proporción en intervengan las tres magnitudes.

Para hacer esto posible, se deberá proceder de la siguiente manera: Se tomará la primera proporción y se multiplicará por la segunda. Esta multiplicación se resolverá entonces multiplicando entre sí los primeros elementos de cada una de las proporciones, mientras que las segundas razones de ambas proporciones también se multiplicarán entre sí. Sin embargo, se tendrá que no se resolverá la multiplicación planteada entre los primeros elementos, mientras que por contar con elementos similares, las otras dos razones podrán suprimir elementos en sí, que lleven entonces a la conformación de una tercera razón. De esta manera, se tendrá una proporción constituida por tres razones, que refieren directamente a cada una de las magnitudes directamente proporcionales que han intervenido:

Primera proporción, cuando se fija la magnitud del número de carpinteros a 6:

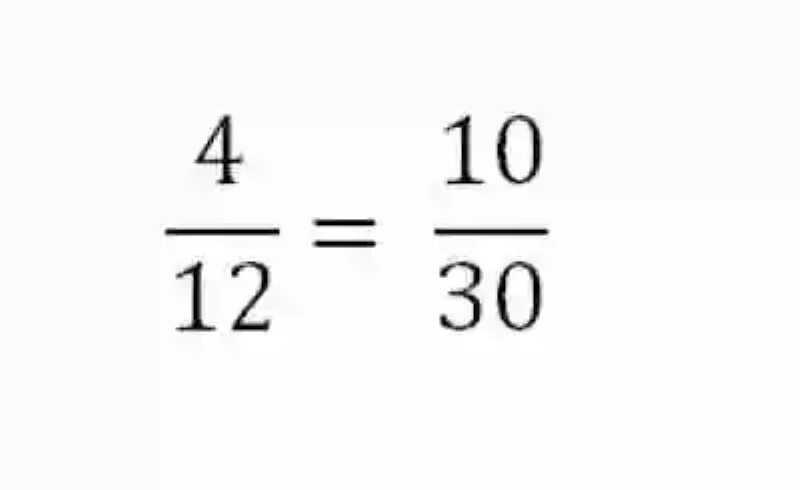
Segunda porción, cuando se fija la magnitud del número de horas trabajadas a 4:

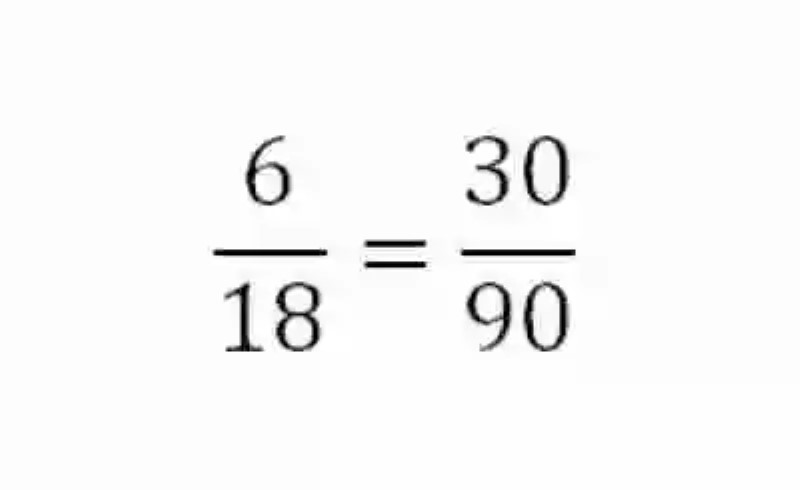
Multiplicación de estas proporciones

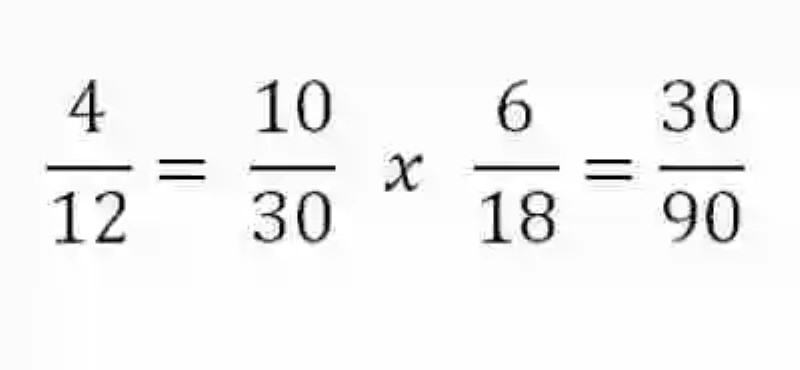
Se multiplican entonces las primeras razones de cada proporción entre sí, así como las segundas razones de estas proporciones:

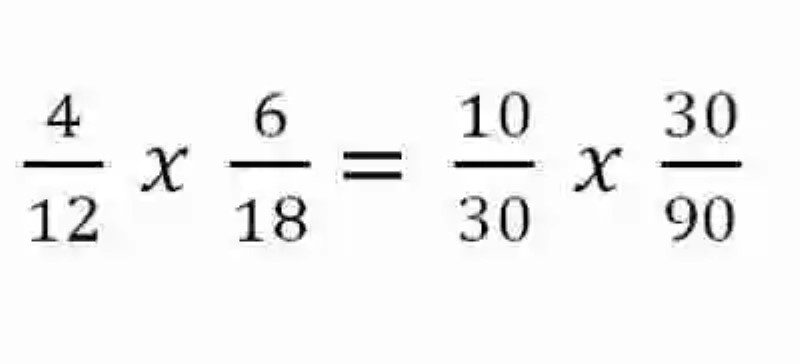
Debido a que hay dos elementos que coinciden en las segundas razones, estos pueden suprimirse, en este caso se elimina el consecuente de la primera razón y el antecedente de la segunda razón:

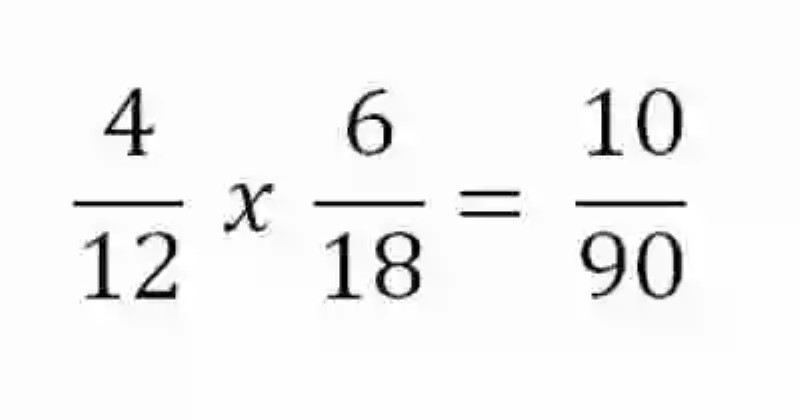
Al hacerlo, se consiguen entonces tres Magnitudes directamente proporcionales. La primera tendrá que ver con la razón conformada o referente al número de horas; la segunda será la razón que dé cuenta del número de carpinteros; y por último  la tercera será la razón que refiera a la tercera magnitud del número de sillas elaboradas.

En consecuencia, se ha logrado entonces, por existir una Magnitud proporcional a otras varias, establecer una proporción en donde pueden verse las razones referentes a las tres magnitudes directamente proporcionales que participan en esta relación.

Imagen: pixabay.com