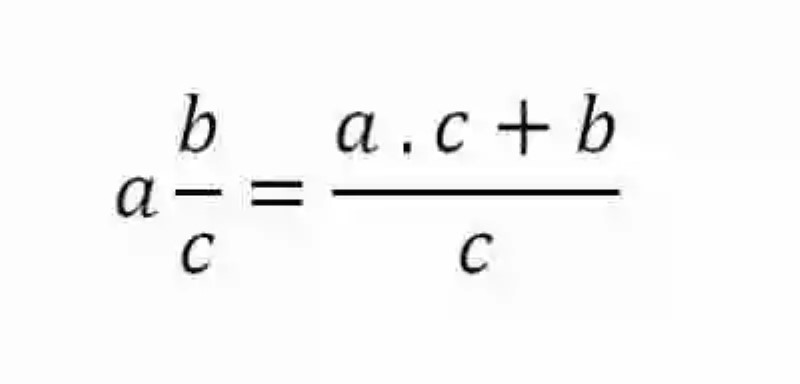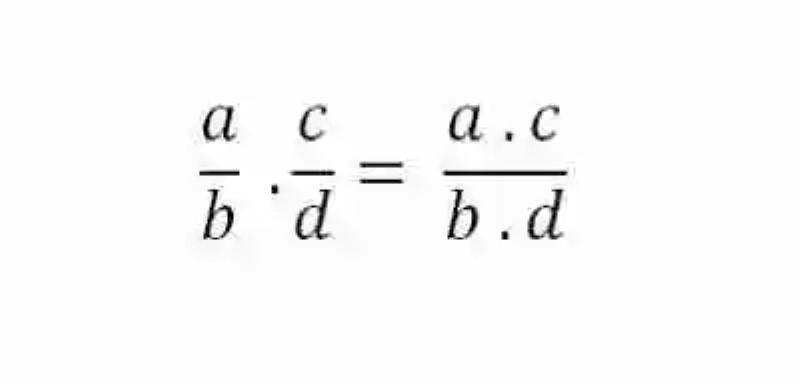Multiplicación de fracciones mixtas

Definiciones fundamentales

En este sentido, resultará entonces pertinente enfocar esta revisión en cuatro nociones precisas: Fracciones, Fracciones impropias, Números enteros y Fracciones mixtas, por ser estas las expresiones inherentes a la operación de multiplicación. A continuación, cada una de ellos:

Fracciones

En consecuencia, se podrá comenzar por decir que las Matemáticas han definido las fracciones como aquellas expresiones, usadas para representar números fraccionarios o cantidades no exactas. Así también, este tipo de expresiones se encontrarán compuestas por dos elementos, cada uno de los cuales se encuentran definidos de la siguiente manera:

• Numerador: en primer lugar, se encontrará el Numerador, el cual se encontrará ubicado, sin excepción, en la parte superior de la fracción, teniendo la responsabilidad de señalar cuántas partes del todo se han tomado, o son representadas por la fracción.
• Denominador: por su parte, el Denominador será el elemento que se encuentra ubicado en la parte inferior de la expresión. Su principal función será la de indicar en cuántas partes se encuentra dividida la unidad o el todo, del cual se han tomado las partes, señaladas por el numerador de la fracción que constituyen.

Fracciones impropias

En otro orden de ideas, será también necesario revisar el concepto de Fracciones impropias, las cuales serán explicadas por los distintos autores como un tipo de fracción, es decir, una expresión matemática, usada para representar cantidades no exactas o fraccionarias, al tiempo que se caracteriza por contar con un Numerador de mayor valor que el Denominador.

Números enteros

En tercer lugar, resultará prudente lanzar luces sobre la definición de Números enteros, los cuales son considerados como elementos a través de los cuales se puede dar cuenta de cantidades exactas o enteras. Este tipo de elemento numérico está constituido por los enteros positivos, sus inversos negativos y el cero, por lo que serán empleados respectivamente para expresar cantidades exactas, ausencia o falta de cantidades enteras específicas, o incluso la ausencia total de cantidad. Estos números son los constituyentes del conjunto numérico Z.

Fracciones mixtas

Por último, será de gran importancia pasar revista sobre la definición de Fracciones mixtas, expresiones matemáticas que son descritas de forma general por los diferentes autores como un tipo de fracción, usadas para señalar ciertas cantidades fraccionarias, y cuya principal característica es estar compuesta por un número entero y un número fraccionario o fracción. Este tipo de expresiones corresponden más al ámbito coloquial que al matemático, y son usadas cuando se quiere dar cuenta de una situación en donde el todo se encuentra constituido por varias unidades, divididas en partes iguales, y de las que se ha tomado por completo una unidad y algunas partes de otra.

Multiplicación de fracciones mixtas

Teniendo presente estas definiciones, quizás ciertamente sea mucho más sencillo abordar la forma correcta en la que debe ser resuelta una operación de multiplicación, que tenga como multiplicando y multiplicador fracciones mixtas. En este caso, las Matemáticas señala que deberán seguirse cada uno de los siguientes pasos:

• En primer lugar, siendo este el método más rápido y sencillo, se procurará convertir cada una de las fracciones mixtas a fracciones impropias, lo cual se hará multiplicando en cada caso el número entero con el denominador de la fracción, para sumar el producto con el numerador, y obtener el numerador de la fracción impropia, dejando como denominador el que la fracción que constituía la expresión mixta tenía originalmente, operación que puede ser expresada de la siguiente manera:

• Seguidamente, se procederá entonces a multiplicar cada una de las fracciones impropias involucradas en la operación, usando el método que se expresa a continuación:

• Al tener el resultado o producto de esta operación, si es posible, se buscará simplificar la fracción impropia, dividiéndola entre su común divisor.
• Finalmente, la fracción simplificada se convertirá nuevamente en una fracción mixta, interpretándose esta como el producto final de la operación.

Ejemplo de cómo multiplicar fracciones mixtas

No obstante, puede que la mejor manera de cerrar una explicación sobre la forma idónea de multiplicar fracciones mixtas, sea a través de la exposición de un ejemplo concreto que permita ver en la práctica cómo debe aplicarse cada procedimiento relacionado a la resolución de este tipo de operaciones, tal como se ve a continuación:

Multiplicar las siguientes fracciones mixtas:

Se procederá en primer lugar a convertir cada una de las fracciones mixtas a fracciones impropias:

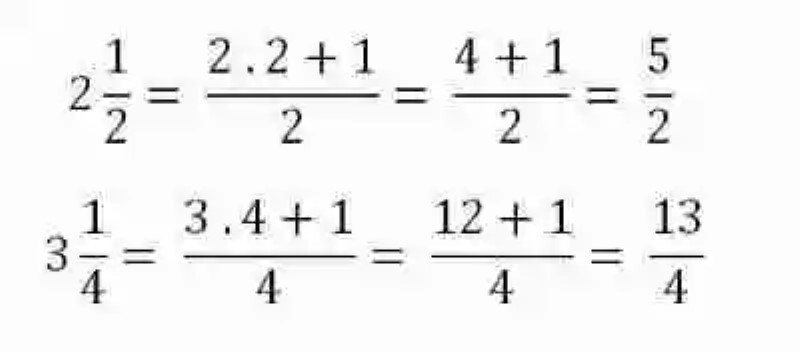
Hecho esto, se multiplicarán las fracciones propias obtenidas:

Al no poder simplificar la fracción, se optará por convertirla en una fracción mixta. Se tomará este como el producto final de la operación:

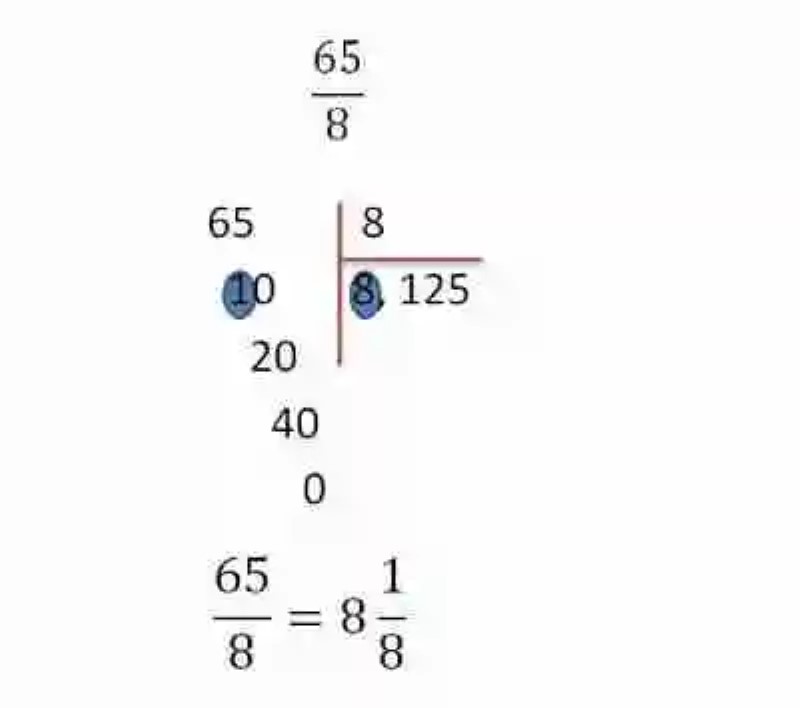
Imagen: pixabay.com