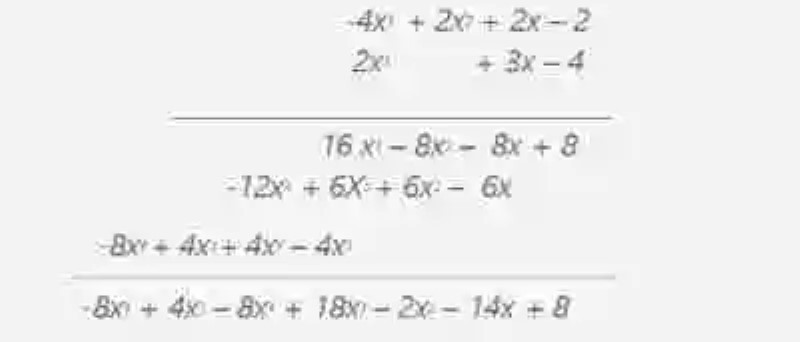
El Polinomio puede definirse como una de las dos principales expresiones algebraicas, la cual está constituida por una suma finita de monomios, términos algebraicos cuya principal característica es la de contar con variables, que se encuentran elevadas a exponentes que en todo momento serán números enteros positivos, incluyendo el cero.
Partes del Polinomio
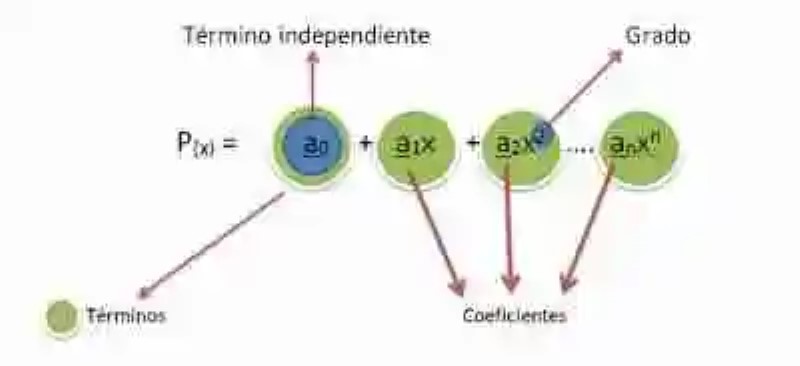
Por ende, cuando se habla de las partes de un polinomio, básicamente se mencionan los monomios que lo comprenden. Sin embargo, el Álgebra elemental también menciona la existencia de cuatro elementos fundamentales, cada uno de los cuales puede ser definido de la siguiente forma:
- Términos: nombre que reciben cada uno de los sumandos que conforman el polinomio. En este sentido, tanto monomios como términos independientes serán llamados de forma general «términos»,
- Términos independientes: será el nombre con el que se designen aquellos elementos numéricos en donde no puede apreciarse la compañía de una variable.
- Coeficientes: igualmente, los coeficientes serán aquellos números que acompañan a la variable, multiplicándola.
- Grado: por último, el grado del polinomio será considerado equivalente al grado de mayor valor que pueda determinarse en los monomios que conforman la expresión. Su función básicamente es servir de guía a la hora de establecer relaciones de semejanza o diferencia entre monomios, así como la de ordenar o clasificar los polinomios.
Multiplicación de Polinomios
Así también, dentro de las distintas operaciones que pueden establecerse entre polinomios, la multiplicación de polinomios puede ser definida como el procedimiento por medio del cual un monomio es multiplicado por cada uno de los términos de un monomio, o también cuando cada uno de los elementos de un polinomio es multiplicado por cada uno de los elementos de otro, a fin de obtener un producto final. No obstante, existen varias formas de abordar esta operación entre polinomios, las cuales pueden explicarse de la siguiente manera.
Un término independiente por un polinomio
El primer caso a estudiar será la operación de multiplicación que puede establecerse entre un término independiente y un polinomio, en cuyo caso, tal como dicta la teoría al respecto se deberá multiplicar dicho término por cada uno de los monomios que conforman el polinomio, a fin de obtener un primer resultado. En caso de que en esta nueva expresión algebraica se encontrarán más de un término para cada grado, se procederá a sumar dichos términos, a fin de obtener la expresión algebraica más reducida posible, tal como se muestra a continuación:
Dada la siguiente operación:
2 . (4x2 + 3x + 3x2 + x3 – 4) =
Se debe multiplicar el primer término por cada uno de los monomios:
(2 . 4x2) + (2 . 3x) + (2 . 3x2) + (2 . x3) – (2.4) =
8x2 + 6x + 6x2 + 2x3 – 8 =
Se procede entonces a la suma de los términos o monomios de igual grado:
(8x2 + 6x2) + 6x + 2x3 – 8 =
14x2+ 6x + 2x3 – 8 =
Por consiguiente, el resultado final será entonces:
14x2+ 6x + 2x3 – 8 =
Un monomio por un polinomio
También puede darse el caso de que los términos que se desean multiplicar sean desiguales en el número de sus términos, siendo uno de los casos más típicos aquel que plantea la multiplicación de un monomio y un polinomio. En dicha circunstancia, el procedimiento a seguir –según las distintas fuentes- será multiplicar dicho monomio por cada uno de los elementos o monomios del polinomio, lo cual se realiza multiplicando los valores de los coeficientes, y sumando los exponentes de las variables. Una vez obtenido el nuevo polinomio, se procederá a identificar cuáles monomios coinciden en cuanto a sus grados, a fin de procurar una suma entre los elementos semejantes, buscando la máxima reducción del término. Un ejemplo de esta tipo de multiplicación, puede ser el siguiente:
Dada la siguiente operación:
2x3 . (3x3 + 2x2 + 2x + 4x3 – 5) =
Se procede a multiplicar el monomio (primer término) por cada uno de los elementos del polinomio (segundo término):
(2x3. 3x3) + (2x3 . 2x2) + (2x2 . 2x) + (2x3. 4x3) – (2x3.5)=
(2.3) x3+3 + (2.2) x3+2 + (2.2) x2+1 + (2.4) x3+3 – (2.5) x3 =
6x6 + 4x5 + 4x3 + 8x6 – 10x3 =
Luego de esto, se suman los polinomios del mismo grado, en caso de que exista más de un término por grado:
(6x6 + 8x6) + 4x5 + (4x3 – 10x3)=
14x6 + 4x5 + (-6x3)=
14x6 + 4x5 – 6x3=
De esta forma, el resultado final será:
14x6 + 4x5 – 6x3=
Polinomio por polinomio
Así mismo, el tercer caso a analizar ocurre cuando las dos expresiones algebraicas a multiplicar pueden ser definidas como polinomios. En este caso, se puede decidir entre algunos de los dos procedimientos que contempla o permite el Álgebra Elemental para dichas operaciones. Y que básicamente pueden definirse a su vez de la siguiente manera:
Primer método: este primer método consiste en multiplicar cada uno de los monomios del primer polinomio por los monomios del segundo polinomio, lo cual se hace –tal como en los casos anteriores- multiplicando sus coeficientes y sumando sus grados. Al lograr esta primera expresión se debe entonces determinar si existe más de un monomio por grado, y en caso de existir esta situación, proceder a sumar los términos semejantes, obteniendo entonces el polinomio más reducido posible. Un ejemplo de esto, lo constituye el siguiente:
Planteada la siguiente multiplicación de polinomios:
(2x3 + 3x – 4) . (2x2 + 2x – 4x3 – 2) =
Se procede a multiplicar cada uno de los términos del primer polinomio con los del segundo:
(2x3.2x2)+(2x3.2x)+(2x3. -4x3)+(2x3. -2)+(3x.2x2)+(3x.2x)+(3x.-4x3)+(3x.-2)+(-4.2x2)+(-4.2x)+ (-4.-4x3) +(-4 .-2) =
(2.2)x3+2+(2.2)x3+1+(2.-4)x3+3+(2.-2)x3+(3.2)x1+2+(3.2)x1+1+(3.-4)x1+3+(3.-2)x+(-4.2)x2+ (-8x)+(-4.-4)x3+(-4.-2)
4x5 + 4x4 + (-8x6)+ (-4x3)+ 6x3 + 6x2+ (-12 x4) + (-6x) + (-8x2)+ (-8x)+ (16x3)+ (8) =
Aplicando la Ley de Signos se procede a resolver los términos que se encuentran dentro de los paréntesis:
4x5 + 4x4 – 8x6 -4x3 + 6x3 + 6x2 – 12x4 – 6x – 8x2 – 8x + 16x3 + 8 =
Se sumarán entonces aquellos términos semejantes, es decir, que posean igual grado:
4x5 + (4x4– 12x4) – 8x6 + (-4x3+6x3+ 16x3) + (6x2 – 8x2) + (– 6x – 8x) + 8=
4x5 + (-8x4) – 8x6 + 18x3 + (-2x2) – 14x + 8 =
4x5 -8x4 – 8x6 + 18x3 -2x2 – 14x + 8 =
Se procede entonces a ordenar el polinomio, en orden descendente, obteniendo como resultado final el siguiente Polinomio completo:
4x5 -8x4 – 8x6 + 18x3 -2x2 – 14x + 8 =
– 8x6 + 4x5– 8x4+ 18x3 -2x2 – 14x + 8 =
Método 2: Sin embargo, existe un segundo método de multiplicación de polinomios, el cual puede resultar incluso un poco más gráfico y práctico. En este sentido, se procederá a ordenar cada uno de los polinomios que deben multiplicarse, colocándolos después uno sobre otro, y procediendo a la multiplicación, anotando el resultada del producto de cada monomio del primer término por el monomio del segundo término en cada línea, las cuales se procederán posteriormente a sumarse, obteniendo un resultado, tal como se muestra en el ejemplo siguiente:
Dada la siguiente multiplicación de polinomios:
(2x3 + 3x – 4) . (2x2 + 2x – 4x3 – 2) =
Se procederá a ordenarlos a ambos en orden descendente, es decir, desde el mayor grado hasta el menor:
(2x3 + 3x – 4) . (-4x3 + 2x2 + 2x – 2) =
Se colocará uno sobre otro, procurando el primer lugar para el polinomio más extenso, procediéndose posteriormente a la multiplicación, tomando para ello el orden del primer número –de derecha a izquierda- del término o polinomio que se ha situado abajo, el cual comenzará a multiplicar al primer término, desde el primer número –de izquierda a derecha- y así con cada término. Los resultados se irán anotando, respetando el orden del polinomio:
En el caso de que los polinomios tengan más de una variable, se escogerá siempre una letra ordenatriz, por la cual ordenar el polinomio, así como para determinar los elementos semejantes a fin de sumarlos, buscando la máxima reducción del término o expresión algebraica.
Imagen: flickr.com
El pensante.com (abril 30, 2017). Multiplicación de polinomios. Recuperado de https://elpensante.com/multiplicacion-de-polinomios/