Quizás lo más recomendable, antes de abordar una explicación sobre los Polígonos simples y los polígonos complejos, sea revisar de forma breve algunas definiciones, que de seguro permitirán entender este tipo de figuras, en su justo contexto geométrico.
Definiciones fundamentales
En consecuencia, puede que también sea conveniente delimitar esta revisión teórica a dos nociones específicas: la primera de ellas, la propia definición de Geometría, pues esto hará posible cobrar conciencia sobre la naturaleza de la disciplina en la cual han surgido los conceptos de estas figuras geométricas. Así también, será necesario tener en cuenta el concepto de Polígono. A continuación, cada una de estas cuestiones:
La Geometría
De esta forma, se comenzará por decir que la Geometría ha de ser entendida como a disciplina que se encarga de estudiar las diferentes formas y figuras, así también como sus diferentes propiedades, como por ejemplo el área, la longitud, el volumen, etc. Por igual, existen fuentes que definen la Geometría como la ciencia de las medidas.
En otro orden de ideas, la Geometría también es considerada como una de las disciplinas más antiguas en el seno de las Matemáticas. Al respecto, quienes así afirman, son de la teoría de que tal como los Números naturales pudieron originarse directamente del concepto de cantidad, manejada por el hombre primitivo, a fin de contabilizar y organizar sus recursos, la Geometría pudo tener como génesis los intentos de estos primeros humanos por entender, medir, replicar o manipular las distintas formas, acciones que les permitieran a la larga hacerse con espacios y herramientas cada vez más eficientes, elementos que a la larga se traducían en mayores posibilidades de sobrevivencia.
Polígono
De igual forma, también será importante reparar en el concepto de Polígono. Sin embargo, antes de abordar esta definición, puede que sea necesario lanzar luces sobre las nociones de Recta y Segmento, por encontrarse directamente relacionadas con la naturaleza y constitución de este tipo de figuras geométricas.
Por consiguiente, la Recta ha de ser explicada como una figura geométrica plana y unidimensional –es decir que cuenta con una sola dimensión- la cual se encuentra compuesta por una secesión infinita de puntos sucesivos, caracterizados por tener la misma dirección. Empero, esto no significa que la Recta cuente con un solo sentido, ya que en realidad tendrá dos de ellos, de acuerdo a las distintas lecturas que pueda tener esta figura geométrica. Así mismo, la Recta será considerada como una figura infinita, pues no contará con principio ni con final.
Con respecto al Segmento, la Geometría ha señalado que este podrá ser considerado como una parte de la Recta, que se encuentra delimitada por dos puntos específicos, que se trazan sobre esta figura geométrica. Sin embargo, a diferencia de la Recta, el Segmento se caracteriza por contar con un punto de inicio y con un punto de final.
Entendidos los conceptos de Recta y Segmentos, se podrá pasar entonces a la definición de Polígonos, los cuales son entendidos como aquellas figuras geométricas planas y bidimensionales, es decir, que cuentan solo con dos dimensiones: ancho y largo, sin que en ellas pueda encontrarse la tercera dimensión de la profundidad.
Por otro lado, los Polígonos son descritos como aquellas figuras geométricas planas y cerradas, que se encontrarán delimitadas por segmentos de rectas, los cuales hacen las veces de lados, siendo conocidos también como bordes. De acuerdo a lo que señalan las diferentes fuentes, estos segmentos, precisamente por originarse de una línea recta, se caracterizan por ser rectos. De hecho cuando una figura plana y cerrada cuenta con alguno de sus lados curvos, no es considerada un polígono como tal. Así mismo, los Polígonos contarán con cuatro distintos elementos: lados, vértices, ángulos y diagonales.
Polígonos simples y polígonos complejos
Una vez se han revisado cada uno de estos conceptos, puede que ciertamente sea mucho más sencillo abordar una explicación sobre los Polígonos simples y los Polígonos complejos, los cuales serán entendidos como aquellos tipos de polígonos que se caracterizan de acuerdo al comportamiento de sus lados, específicamente si estos se cruzan o no con otros. A continuación, una breve descripción de cada uno de ellos:
Polígonos simples
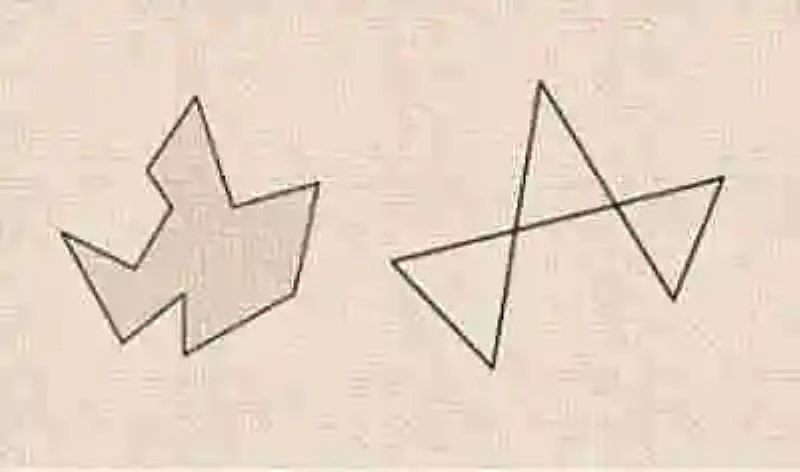
De esta manera, los Polígonos simples han sido explicados por la Geometría como aquellas figuras geométricas planas y cerradas, conformadas por segmentos de rectas, que le sirven de límites, y que a su vez –en el caso de los polígonos simples- no cuentan con la particularidad de cruzarse con ningún otro lado, ni siquiera consigo mismo. Un ejemplo de cómo lucen este tipo de polígonos serían los siguientes:

Polígonos complejos
En segunda instancia, dentro de los distintos tipos de polígonos que existen se encontrarán los polígonos complejos, conocidos también como polígonos cruzados. Estos se caracterizarán por ser figuras geométricas planas, delimitadas igualmente por segmentos de rectas, los cuales constituyen los lados del polígono, y que se caracterizarán por cortarse o cruzarse con otros lados. Un ejemplo de cómo lucen este tipo de polígonos serán los siguientes:

Imágenes: wikimedia.org
El pensante.com (junio 26, 2018). Polígonos simples y polígonos complejos. Recuperado de https://elpensante.com/poligonos-simples-y-poligonos-complejos/