
Es probable que antes de abordar la definición de Polinomio ordenado, así como las distintas operaciones involucradas en su disposición, sea necesario recordar la definición misma del polinomio, a fin de poder entender la primera categoría dentro de su contexto preciso.
Definición de polinomio
En este sentido, la mayoría de las fuentes sobre álgebra indican que el polinomio puede ser concebido como una suma finita de monomios, los cuales se caracterizan a su vez por tener literales o variables que se encuentran siempre elevados a números enteros positivos, incluyendo el cero. Así mismo, además de la suma, los polinomios también contemplan operaciones de suma y multiplicación, siendo la división la única operación no permitida. Con respecto a los elementos que conforman el polinomio, el Álgebra elemental apunta a que básicamente se trata de monomios o términos algebraicos, no obstante, se pueden identificar cuatro elementos fundamentales, tal como se muestra en la gráfica y las definiciones que se ofrecen a continuación:
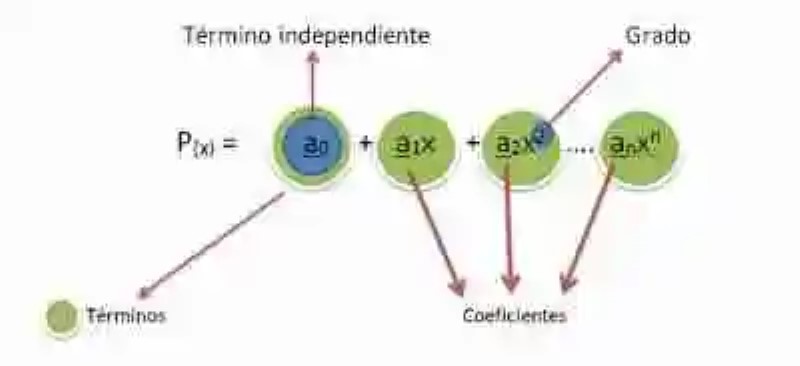
- Términos: con este nombre, se signan cada uno de los sumandos del polinomio, es decir, tanto monomios como términos independientes.
- Términos independientes: por su parte, los términos independientes serán aquellos elementos numéricos que no se encuentren acompañados de una variable.
- Coeficientes: así mismo, los coeficientes serán aquellos elementos numéricos que acompañen la variable, indicando cuál es la cantidad por la que debe multiplicarse la variable, en caso de asumir un valor numérico, o llegar a ser despejada.
- Grado: finalmente, el grado del polinomio vendrá dado por el valor del máximo exponente que pueda identificarse en los monomios que conforman la expresión (en caso de los polinomios de una variable) o del máximo grado absoluto que pueda verse en sus monomios (si el polinomio llega a tener más de una variable). De acuerdo a lo que señalan la mayoría de las fuentes teóricas, el Grado del polinomio es un elemento de esta expresión cuya misión principal es la de servir de valor de referencia a la hora de determinar una clasificación en base al grado (polinomio de primer grado, de segundo grado, etc.) o un orden ascendente o descendente.
Polinomio ordenado
En este sentido, uno de los tipos de polinomio en donde el grado juega un papel crucial es el polinomio ordenado, el cual puede ser definido básicamente como aquel polinomio que ha sido dispuesto según el orden de sus grados, bien sea de forma ascendente o de forma descendente, es decir, del grado mayor al menor, o del grado menor al mayor (teniendo en cuenta de que al término independiente siempre se le asignará un grado igual a cero) tal como se muestra a continuación:
P(x) = x4 – x3– 8x2– x – 6
P(x) = – 6 – x – 8x2 – x3 + x4
Ejemplos en donde se puede observar dos formas de organización, tanto ascendente como descendente de un polinomio completo, de cuarto grado. No obstante, no siempre los polinomios cuentan con una serie ininterrumpida de grados, e incluso no siempre se presentan con una sola variable. Sin embargo, esto no quiere decir que no puedan ser ordenados, a continuación algunos de los casos más comunes que pueden presentarse en el momento de ordenar un polinomio:
Polinomio incompleto de una sola variable
De esta manera, puede ocurrir que el polinomio presentado, además de tener una sola variable, esté incompleto, es decir, que sus grados no formen una secuencia numérica. En este caso, igualmente se debe proceder a identificar cuál es el grado mayor, a fin de ir disponiendo la expresión algebraica según el orden decidido. Una forma de ilustrar esto puede ser tomando como referencia el polinomio que se presenta a continuación:
P(x) = 3x2 + x – 4 + 3x5 + 4 + 8
En este sentido, lo primero que se hará será identificar el grado mayor, encontrando que este corresponde a cinco, es decir, que es un polinomio quíntico, De esta forma, se procederá a ordenarlo de forma descendente, no importa que existan grados que no existan:
P(x) = 3x5 +3x2 + x – 4 + 4 + 8
De esta forma, se obtendrá un polinomio ordenado, de mayor a menor, en donde cada elemento va signado según la posición que ocupa por su grado. Igualmente, se puede expresar otra organización, que vaya de menor a mayor:
P(x) = – 4 + 4 + 8 + x +3x2 + 3x5
Polinomio incompleto de más de una variable
Igualmente puede ocurrir que el polinomio dado, además de ser un polinomio incompleto, posea también más de una variable, en cuyo caso será necesario identificar cuál será la variable o letra ordenatriz por la cual se regirá el ordenamiento del polinomio. Por ejemplo:
Dado el siguiente polinomio
P(x)= xy2 – x + 3x2y4 – y2+ 8
Se procederá a ordenarlo según cada uno de los grados de las distintas variables, teniendo entonces al menos cuatro tipos de disposición:
Letra ordenatriz x
orden descendente → P(x) = xy2 + 3x2y4 – x – y2 + 8
orden ascendente → P(x) = 8 – x + xy2 + 3x2y4 – y2
Letra ordenatriz y
orden descendente → P(x) = 3x2y4 – y2 + xy2 – x + 8
orden ascendente → P(x) = 8 – y2 + 3x2y4 – x + xy2
Imagen: flickr.com
El pensante.com (abril 23, 2017). Polinomio ordenado. Recuperado de https://elpensante.com/polinomio-ordenado/