
Tal vez lo más conveniente, antes de abordar una explicación sobre cada una de las distintas Posiciones relativas que pueden asumir entre ellas dos circunferencias, sea revisar de forma breve la propia definición de este tipo de curva, en base a la cual se establecen dichas posiciones.
La circunferencia
En este sentido, se comenzará por decir que la Geometría ha definido la Circunferencia como un tipo de línea curva, plana y cerrada, que se dispone en torno a un centro, el cual se caracteriza por encontrarte a una distancia equidistante de todos los puntos que conforman la circunferencia. Así mismo, la Geometría ha explicado que la Circunferencia contará con seis distintos elementos: el Centro, el Radio, el Diámetro, la Cuerda, el Arco y la Semicircunferencia.
Por otro lado, la Geometría ha señalado que en ocasiones el común denominador de las personas opta por confundir los conceptos de Circunferencia, Círculo y Esfera. En este orden de ideas, la disciplina geométrica refiere sobre la necesidad de comprender que la Circunferencia es una línea curva y cerrada, que se ubica en torno a un centro, mientras que el Círculo será el espacio geométrico, delimitado por esta curva. En el caso de la Esfera, esta se distinguirá por contar con volumen.
Posición relativa de dos circunferencias
Una vez revisado el concepto de Circunferencia, quizás sea mucho más sencillo aproximarse a cada una de las posiciones relativas, que pueden asumir dos circunferencias, que coincidan en un mismo plano. Al respecto, la Geometría considera que existen siete posibles disposiciones, las cuales han sido descritas de la siguiente manera:
Circunferencias exteriores
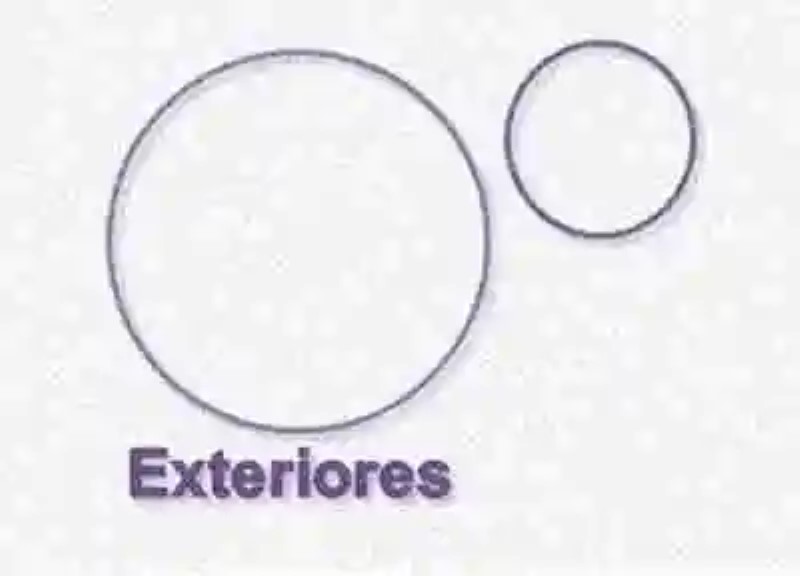
La primera posición relativa que la Geometría señala en torno a dos circunferencias será la de las Circunferencias exteriores. En este caso, esta disciplina señala que dos circunferencias son consideradas como exteriores cuando entre ellas no existe un solo punto de contacto. Así mismo, la Geometría considera igualmente la distancia que existe entre los centros de cada una de estas circunferencias, determinando que si esta es mayor que la suma de los radios que posee cada circunferencia, entonces sí se trata de circunferencias exteriores. A continuación, un ejemplo de este tipo de posición relativa:
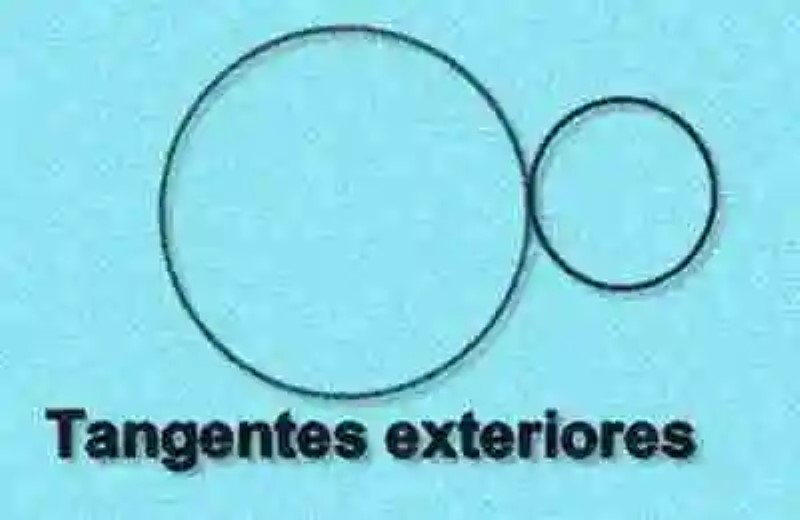
Circunferencias tangentes exteriormente
En segundo lugar, la Geometría distingue, en cuanto a las posiciones relativas que pueden tener dos circunferencias, las Circunferencias tangentes exteriormente. En este orden de ideas, la disciplina geométrica señalará que esta posición puede ser definida como aquella que se da cuando dos circunferencias coinciden o se tocan en solo uno de sus puntos, manteniendo sin contacto los otros, e incluso siendo todos los puntos de una de las circunferencias totalmente exteriores a la otra con la que comparte este único punto. De igual manera, los centro de estas circunferencias se encuentran a una distancia que coincide al total de la suma que existe entre sus radios. A continuación, un ejemplo de este tipo de posición relativa:
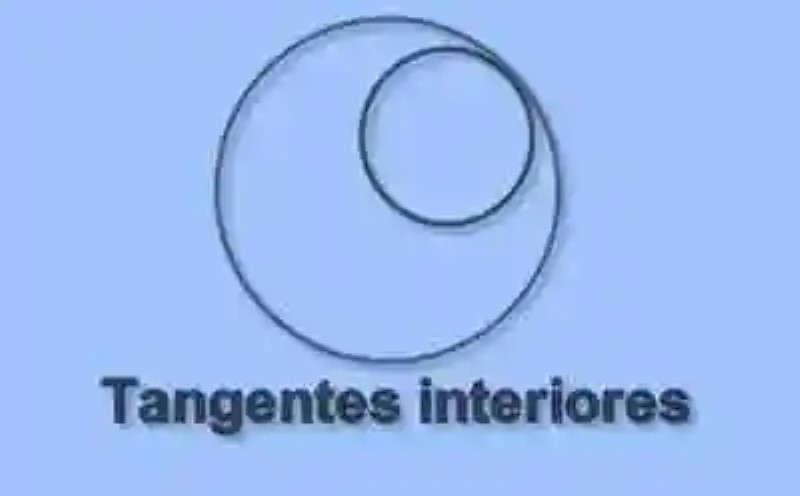
Circunferencias tangentes interiormente
Así también puede suceder que dos circunferencias coincidan en uno de sus puntos, al tiempo que los puntos de una de estas circunferencias se encuentran comprendidos en la otra circunferencia con las que establece esta posición relativa. Por otro lado, la disciplina geométrica indica que estas circunferencias presentan una distancia entre sus centros, que resulta equivalente a la diferencia que existe entre sus respectivos radios. Al encontrarse una circunferencia dentro de otra, se desprende también como característica de las curvas involucradas en esta posición relativa que una cuenta con un radio menor a la circunferencia en donde se encuentra contenida. Este tipo de posición relativa lucirá de la siguiente forma:
Circunferencias secantes
Otra de las posiciones relativas que pueden establecerse en torno a dos circunferencias será la Circunferencias secantes, las cuales se caracterizarán por coincidir en cuanto a dos de sus puntos. Así mismo, la Circunferencias secantes contarán con una distancia entre sus respectivos centros, que siempre resultará menor al total que se obtiene al sumar los radios de cada una de ellas.

Circunferencias interiores excéntricas
También puede ocurrir que una circunferencia se encuentre dentro de otra, sin que exista entre ellas un solo punto en común. Así mismo, tendrán distintos centros, los cuales se encontrarán a una distancia mayor a cero, pero que a su vez resultará menor al valor absoluto de la diferencia que se puede obtener al restar sus respectivos radios.
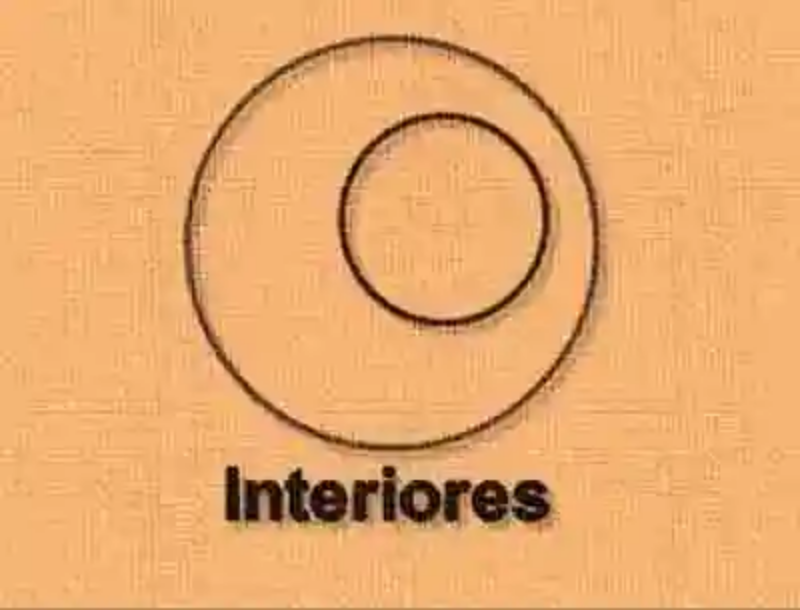
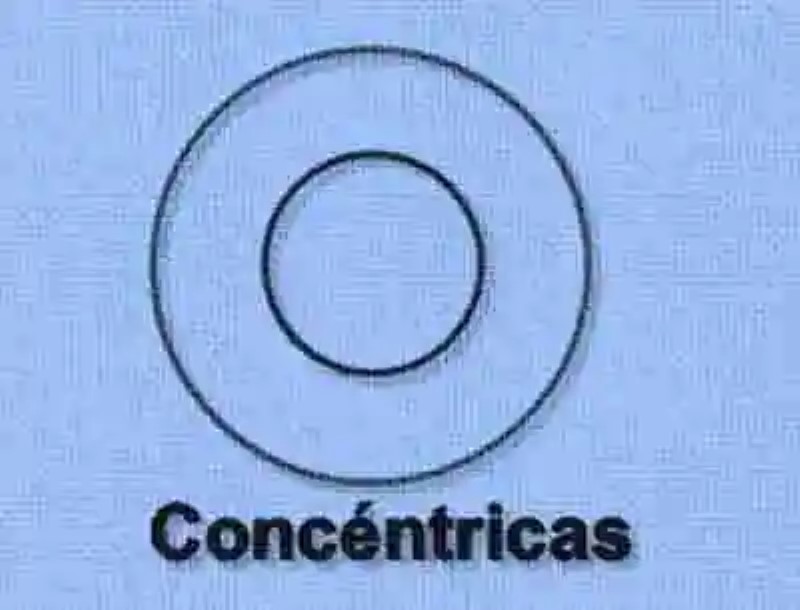
Circunferencias interiores concéntricas
Por igual, será necesario tener en cuenta el concepto de Circunferencias interiores concéntricas, las cuales han sido explicadas como aquellas circunferencias, que se caracterizan por encontrarse una dentro de la otra, al tiempo que comparten el mismo centro. En consecuencia, la distancia entre los centro de estas circunferencias interiores concéntricas es igual a cero. En cuanto a sus radios, estos contarán con distintas medidas.
Circunferencias coincidentes
Por último, al hablar de las posiciones relativas que pueden establecerse entre dos circunferencias, la Gramática explica las Circunferencias coincidentes, las cuales serán entendidas como aquellas circunferencias que coinciden en cuanto a su centro, así también como en cada uno de sus puntos. En este sentido, la disciplina geométrica indica que si dos circunferencias son diferentes en cuanto a sus respectivos radios, entonces solo podrán coincidir en cuanto a dos puntos, mientras que si presentan igual radio y son coincidentes, lo hacen en todos sus puntos.
Imagen: pixabay.com
El pensante.com (mayo 31, 2018). Posición relativa de dos circunferencias. Recuperado de https://elpensante.com/posicion-relativa-de-dos-circunferencias/