Tabla de contenido
Antes de abordar cada una de las diferentes Posiciones relativas de una recta respecto a una circunferencia, puede que resulte conveniente revisar algunas definiciones, que permitirán entender cada una de estas posiciones en su contexto geométrico específico.
Definiciones fundamentales
En este sentido, puede que también sea pertinente delimitar esta revisión teórica a dos nociones específicas: la Circunferencia y la Recta, por ser respectivamente la curva y el ente geométrico, que se relacionan y disponen de distintas formas, creando las diferentes posiciones, que la Geometría denomina como Posiciones relativas entre ellas. A continuación, cada una de estas definiciones:
La Circunferencia
De esta manera, se comenzará por decir que la Circunferencia ha sido definida por la Geometría como una línea curva, plana y cerrada, que se dispone alrededor de un centro, el cual se caracteriza a su vez por estar ubicado a una distancia equidistante a todos los puntos que conforman esta curva cerrada. Así también, la disciplina geométrica ha señalado que la Circunferencia contará con seis elementos principales: el Centro, el Radio, el Diámetro, la Cuerda, el Arco y la Semicircunferencia.
Por otro lado, existen fuentes que señalan cómo en ocasiones el común denominador de las personas tienden a confundir la Circunferencia, el Círculo y la Esfera, lo cual constituye un error conceptual. En este orden de ideas, la Geometría señala que lo mejor será entender que la Circunferencia es una línea curva y cerrada que se dispone alrededor de un centro, mientras que el Círculo será entendido como el espacio geométrico, que se encuentra delimitado por esta curva. En el caso de la Esfera, su principal rasgo distintivo es el de contar con volumen.
La Recta
En segunda instancia, será también necesario lanzar luces sobre el concepto de la Recta, la cual ha sido definida por los distintos autores como una figura geométrica unidimensional, explicada también como una sucesión infinita de puntos, dispuestos en la misma dirección.
Así también, la Geometría ha explicado la Recta como la distancia más corta que puede encontrarse entre dos puntos, ubicados en un plano. De igual manera, la disciplina geométrica ha explicado que la Recta será la única figura geométrica que puede pasar por medio de dos puntos, al tiempo que esta disciplina señala que entre dos puntos solo puede pasar una recta a la vez. Entre otras de las características con las que cuenta la Recta se pueden encontrar las siguientes:
- Al estar conformada por una sucesión infinita de puntos, la Recta en sí misma es definida como una figura geométrica unidimensional e infinita, pues no tendrá ni principio ni final.
- En segundo lugar, pese a estar conformada por una secesión de puntos, dispuestos en la misma dirección, la Recta en realidad puede contar con dos distintos sentidos, lo cual dependerá del sentido en el que se lea este figura.
- Finalmente, la Recta también se distinguirá por ser representada por una letra minúscula.
Posición relativa de una Recta respecto a una Circunferencia
Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación hacia las distintas posiciones que una Recta puede asumir en relación a una circunferencia, con la que coincida en un mismo plano, y que de acuerdo a la Geometría, básicamente pueden clasificarse en tres posiciones relativas. A continuación, una breve descripción de cada una de ellas:
Recta exterior a una circunferencia
La primera de ellas, será aquella en donde la Recta se encuentre fuera del área delimitada por la Circunferencia, o incluso de la misma línea curva que la conforma. En este caso, la Geometría toma como principal criterio, a la hora de determinar esta posición relativa, que la Recta no tenga o coincida con ninguno de los puntos de la Circunferencia. Así mismo, se toma en cuenta la distancia en que se encuentra la Recta respecto al centro de la Circunferencia, si esta medida en mayor a la longitud del Radio, entonces se considera que la Recta se encuentra ubicada por fuera de la Circunferencia. A continuación, un ejemplo de esta posición relativa entre una Recta y la Circunferencia:

Recta tangente a una Circunferencia
Otra de las posiciones relativas que pueden asumir una Recta y una Circunferencia es aquella que convierte a la Recta en una tangente de la Circunferencia, situación que se dará cuando la Recta toca o intercepta en un punto específico –el cual es llamado por la Geometría como Punto de tangencia- a la circunferencia. Así mismo, para identificar este tipo de posición relativa, la Geometría toma en cuenta la distancia a la que se encuentra la Recta del centro de la Circunferencia, considerando que esta es tangente si la distancia coincide plenamente con el radio de esta línea curva cerrada. Un ejemplo de este tipo de posición relativa será el siguiente:
Recta secante a una Circunferencia
Por último, dentro de las distintas posiciones relativas que existen entre una Recta y una Circunferencia, se encontrará la Recta secante a una Circunferencia, la cual será definida como la situación en que una Recta coincide en dos puntos distintos de la curva cerrada que constituye la circunferencia, al tiempo en que la distancia a la que se encuentra la Recta del centro, es menor al Radio de la Circunferencia. A continuación, un ejemplo de este tipo de posición relativa:
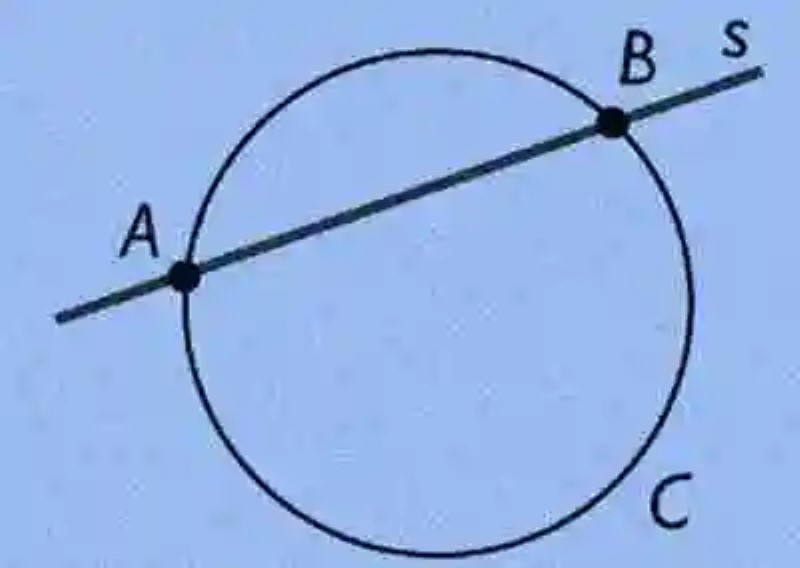
Imagen: pixabay.com
El pensante.com (mayo 30, 2018). Posición relativa de una recta respecto a una circunferencia. Recuperado de https://elpensante.com/posicion-relativa-de-una-recta-respecto-a-una-circunferencia/