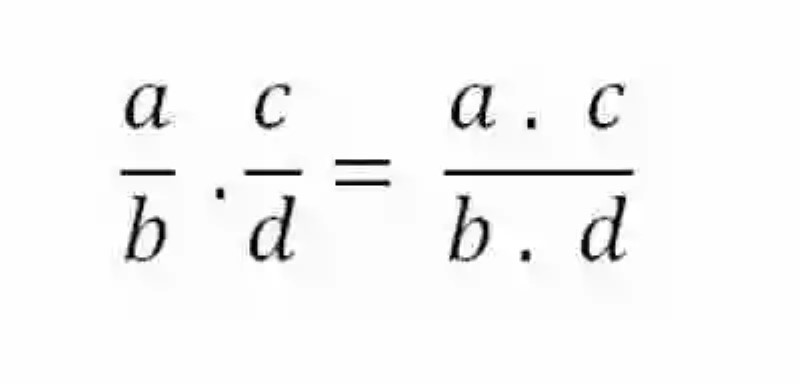Tal vez lo más recomendable, antes de avanzar en una explicación sobre la forma correcta de resolver una operación para determinar la Potencia de un producto de fracciones, sea revisar brevemente algunas definiciones, que permitirán entender este procedimiento matemático en su contexto preciso.
Definiciones fundamentales
En este sentido, quizás lo mejor sea delimitar esta revisión teórica a cuatro nociones específicas: Fracciones, Multiplicación de fracciones, Potenciación y Potencias de base racional, por ser estas las expresiones y operaciones directamente relacionadas con el procedimiento de determinar cuál es la potencia del producto de dos o más fracciones. A continuación, cada una de estas definiciones:
Fracciones
En primer lugar, se podrá comenzar por decir que las Matemáticas han definido las fracciones, de forma general, como un tipo de expresión matemática, por medio de la cual se da cuenta de números fraccionarios o racionales, es decir, que las fracciones serán empleadas –siempre y sin excepción- para dar cuenta de cantidades no enteras o no exactas. Así también, la disciplina matemática ha señalado que estas expresiones se encontrarán constituidas por dos elementos, explicados a su vez de la siguiente manera:
- Numerador: por un lado, el Numerador será el elemento que ocupe o conforme la parte superior de la fracción. Su tarea será indicar cuántas partes del todo han sido tomadas, o son representadas por el Numerador.
- Denominador: en cuanto al Denominador, las Matemáticas lo conciben como el elemento que ocupa la parte inferior de la fracción, siendo su misión principal la de señalar en cuántas partes se encuentra dividido el total o la unidad, de la cual la fracción señala solo algunas.
Multiplicación de fracciones
De igual forma, se deberá prestar atención a la definición de Multiplicación de fracciones, las cuales han sido explicadas como un tipo de operación matemática dirigida a establecer cuál es el producto que se obtiene al sumar por sí misma una fracción, tantas veces como le señale una segunda expresión fraccionaria, de ahí que este procedimiento pueda ser interpretado también como una suma abreviada.
En referencia a la forma correcta de dar respuesta a una operación de este tipo, las Matemáticas señalan que en realidad la Multiplicación de fracciones constituyen la operación más sencilla en donde están involucradas este tipo de expresiones, pues se necesitará simplemente multiplicar el numerador por el numerador y el denominador por el denominador, lo cual podrá representarse matemáticamente hablando de la siguiente manera:
Potenciación
En tercer lugar, será también necesario pasar revista sobre el concepto de Potenciación, el cual ha sido explicado por las distintas fuentes como una operación matemática, cuyo principal propósito será determinar cuál es el producto de multiplicar, por sí mismo, un número –que hace las veces de base- tantas veces como señale un segundo elemento numérico –que por su parte ejercerá como exponente-, de ahí que la Potenciación haya sido explicada también como una multiplicación abreviada.
Potencias de base racional
Finalmente, resultará igualmente pertinente el tomar en cuenta el concepto de Potencias de base racional, las cuales podrán ser entendidas como aquellas operaciones de potenciación en donde la base está constituida por una fracción. En consecuencia, las Potencias de base racional plantearán el objetivo de conocer cuál es el producto de multiplicar por sí misma una fracción, tantas veces como señale el número natural que haga las veces de exponente.
Así mismo, las Matemáticas señalan que para resolver este tipo de operaciones, será necesario aplicar la fórmula general de Potencias de base racional, la cual consiste en elevar por separado cada elemento de la fracción al exponente que indica la operación, procedimiento que podrá ser expresado matemáticamente de la siguiente forma:
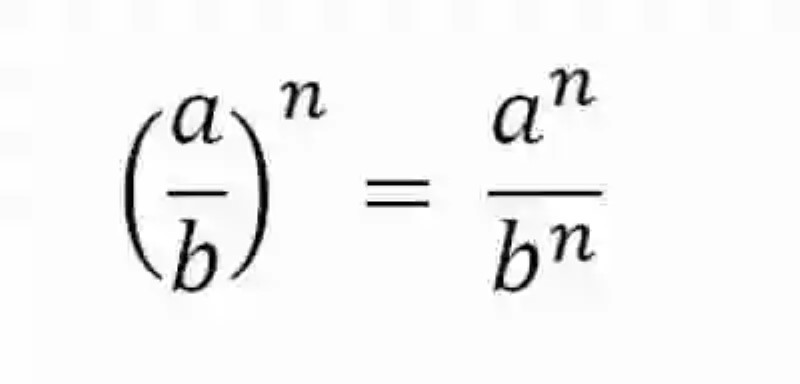
Potencia de un producto de fracciones
Teniendo presente estas definiciones, quizás ciertamente resulte mucho más sencillo abordar la definición de Potencia de un producto de fracciones, la cual puede ser entendida como una operación matemática, destinada a determinar cómo se resuelve todo procedimiento que plantee la elevación de una multiplicación de fracciones a un exponente específico.
En este orden de ideas, la disciplina matemática señala que lo más conveniente será elevar cada uno de los factores que constituyen la multiplicación al exponente involucrado en la operación, para después elevarlos cada uno individualmente. Esta operación podrá ser expresada matemáticamente de la siguiente forma:

Ejemplo de cómo resolver la Potencia de un producto
No obstante, puede que la forma más eficiente de completar una explicación sobre la forma correcta en que debe resolverse toda operación en donde un producto o multiplicación de fracciones hayan sido elevadas a un exponente en común, sea exponer un ejemplo concreto, que permita ver en la práctica cómo se cumplen cada uno de los pasos señalados por la teórica matemática, tal como puede verse en el siguiente ejercicio:
Resolver la siguiente operación:
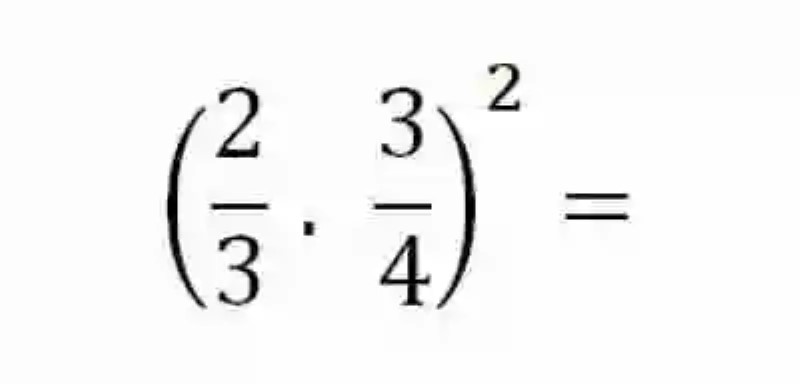
Una vez se ha revisado la operación, se determina que se trata de la Potencia de un producto, por lo que para resolverla será necesario elevar por separado cada factor al exponente planteado:

Planteada así la operación, se deberá resolver cada potencia, elevando por separado cada elemento de las fracciones al exponente que le corresponde:
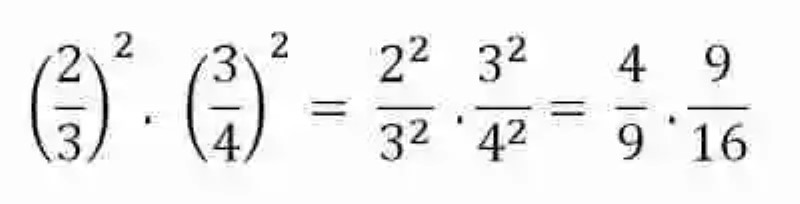
Llegado a este punto, se deberá realizar entonces una multiplicación de fracciones, para lo que se multiplican los elementos entre sí, es decir, numerador por numerador, y denominador por denominador:
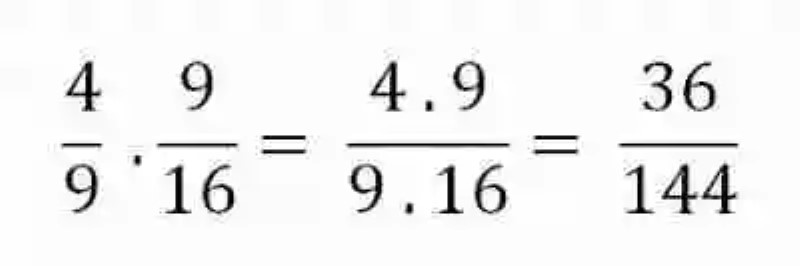
Obtenido un producto, se deberá revisar si la fracción puede ser simplificada:

Llegada a esta fracción, considerada como la forma más reducida, se considera entonces que se ha resuelto la operación:
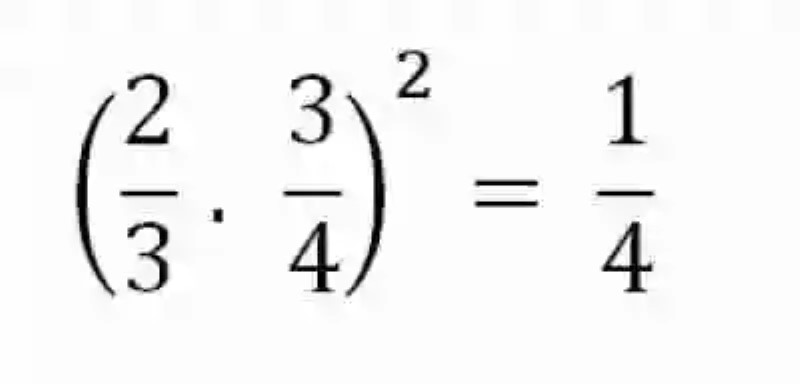
Imagen: pixabay.com
El pensante.com (febrero 21, 2018). Potencia de un producto de fracciones. Recuperado de https://elpensante.com/potencia-de-un-producto-de-fracciones/