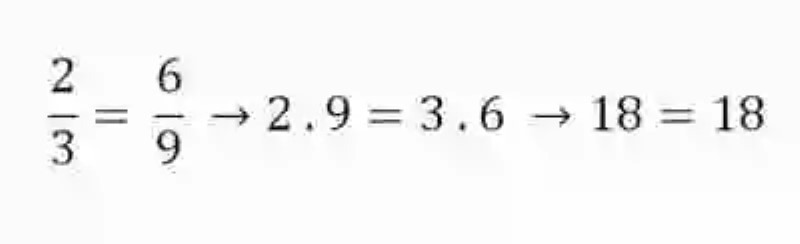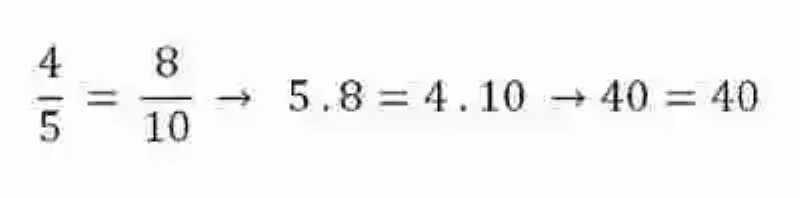Tal vez lo más prudente, antes de abordar una explicación sobre la Primera propiedad que puede observarse en las Proporciones, sea revisar de forma breve algunas definiciones, que de seguro permitirán entender esta ley matemática, dentro de su justo contexto.
Definiciones fundamentales
En este sentido, puede que lo más conveniente sea delimitar esta revisión teórica a tres definiciones específicas: Cociente, Razones y Proporciones, por encontrarse entonces directamente relacionadas con la propiedad matemática que se estudiará posteriormente. A continuación, cada una de estas definiciones:
Cociente
De esta manera, se comenzará por decir que las distintas fuentes coinciden en asumir el Cociente como uno de los cuatro elementos de la División. En específico, el Cociente será entendido como el resultado de una división entre un Dividendo y un Divisor, por lo que entonces este elemento dará cuenta explícitamente de las veces en que el Divisor se encuentra contenido en el Dividendo.
Por ejemplo, si se dividiera el dividendo 10 entre el divisor 5, el resultado o cociente de esta operación sería igual a 2, lo que indicaría entonces que 5 (el divisor de esta operación) se encuentra contenido 2 veces (según señala el cociente) en 10 (es decir en el dividendo).
Razones
Por su parte, las Razones han sido explicadas por la disciplina matemática como el cociente de dos números, elemento este que puede ser expresado de la siguiente manera:
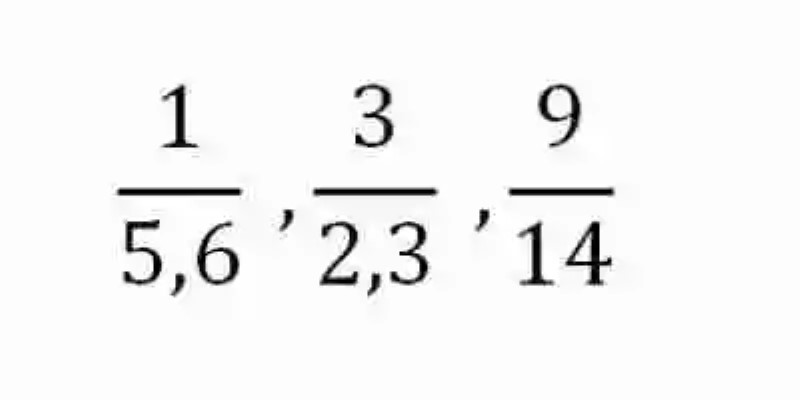
Sin embargo, la forma en que es expresada una razón no ha de ser confundida con una fracción, siendo la principal diferencia entre estas que la fracción –expresión de las partes que son tomadas de una unidad dividida en partes iguales- se encuentra constituidas por un numerador y un denominador que siempre serán números enteros, mientras que, en las razones, el antecedente y el consecuente pueden estar conformados por números decimales.
Proporciones
Por último, las Proporciones puede ser entendidas como la relación de igualdad que existe entre dos razones. Por ejemplo, si se tuviese la siguiente aplicación lineal: y = 2x, y se deseara aplicar a la siguiente razón específica:
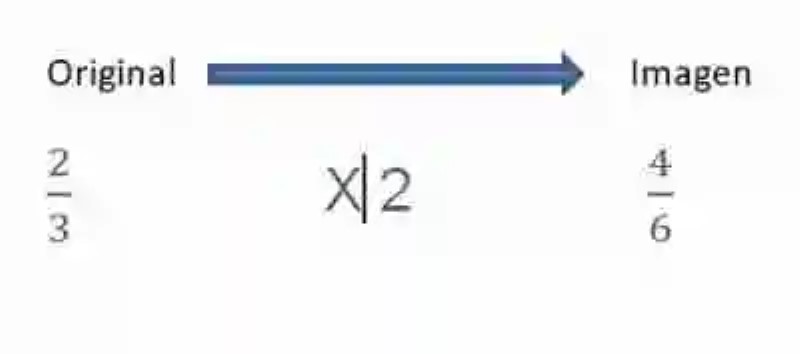
Si se resolvieran las dos razones, es decir, la original y su imagen, se hallaría el mismo cociente, por lo que entonces estas razones pueden considerarse iguales, por ende entre ellas existe una Proporción, que además se mantiene de forma constante en la serie de razones iguales que pueden determinarse.
Primera propiedad de las Proporciones
Una vez se han explicado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar una revisión sobre la Primera propiedad, que las Matemáticas han señalado en las Proporciones. En este sentido, esta disciplina indica que siempre que existan dos razones iguales, es decir, una proporción, el producto de sus medios resultará siempre igual al producto de sus extremos.
Al respecto, es importante señalar que los medios de una proporción serán identificados como el antecedente de la primera razón y el consecuente de la segunda, mientras que los extremos se encontrarán conformados por el consecuente de la primera razón y el antecedente de la segunda. Esta relación o propiedad matemática puede ser expresada de la siguiente forma:
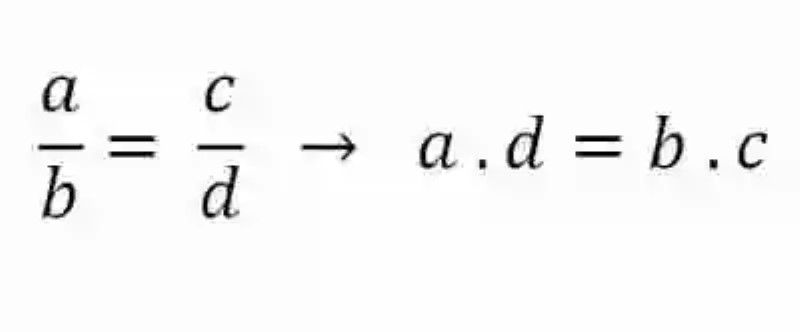
Ejemplo de la Primera propiedad de las proporciones
Sin embargo, puede que la mejor forma de asimilar la Primera propiedad que puede encontrarse en las proporciones sea a través de un ejemplo concreto, que permita ver si realmente lo dicho por la teoría es real en la práctica.
Comprobar en las siguientes proporciones la Primera propiedad:
Para cumplir con lo dictado por este planteamiento, lo mejor será multiplicar entonces los medios por los externos:
Utilidad de la Primera propiedad de las proporciones
Así mismo, las Matemáticas han señalado que esta propiedad matemática cuenta con una importante utilidad, consistente en ofrecer la posibilidad de determinar cuál es el término desconocido de una razón que estableciera proporción con otra. Por ejemplo, si se tuviera la siguiente proporción:
Y se descubriera entonces que se desconoce el consecuente de la segunda razón, se procedería a hallar el producto de los extremos, pues este sería en teoría igual al que se obtendría multiplicando los medios:
Al hacerlo, se encuentra que el producto de los extremos es 40, por lo que entonces el consecuente de la segunda razón o el elemento de los extremos por determinar es el producto de los medios entre el antecedente de la primera razón, o el único elemento de los extremos que se conoce:
40 : 4 = 10
Se tiene entonces que el número desconocido es 10. Si se quisiera comprobar si realmente es el número que corresponde al valor desconocido en la segunda proporción, bastaría entonces con aplicar la Primera propiedad de la Proporción, y multiplicar los medios y los extremos para descubrir si ciertamente resultan iguales:
Efectivamente se ha podido comprobar que el número desconocido en estas proporciones es el 10, puesto que al aplicar la Primera propiedad de la proporción el producto de los extremos resulta igual al producto de los extremos, más allá de comprobar también que ambas razones son iguales, y por ende proporcionales.
Imagen: pixabay.com
El pensante.com (octubre 19, 2018). Primera propiedad de las proporciones. Recuperado de https://elpensante.com/primera-propiedad-de-las-proporciones/