
Quizás lo más conveniente, previo a abordar una explicación sobre la manera correcta de resolver una operación que plantee el producto de potencias de fracciones que coinciden en cuanto a sus bases, sea revisar de forma breve algunas definiciones, que permitirán entender este procedimiento en su justo contexto matemático.
Definiciones fundamentales
En este sentido, puede que también sea prudente enfocar esta revisión teórica en tres conceptos específicos: Potenciación, Fracciones y Potencias de base racional, por ser las nociones directamente relacionadas con la operación que implica multiplicar potencias de fracciones, en donde los distintos factores presentan igual base. A continuación, cada una de estas definiciones:
Potenciación
De esta manera, se comenzará por decir que las distintas fuentes matemáticas optan de forma general por señalar la Potenciación como una multiplicación abreviada, la cual tendrá como propósito entonces determinar cuál es el producto que se obtiene al multiplicar un número por sí mismo tantas veces como señala el segundo elemento numérico involucrado en la operación. Esta operación puede ser representada matemáticamente de la siguiente forma:
an = an1 . an2 . an3 …
Por igual, la disciplina matemática señala que la Potenciación podrá ser comprendida como una operación conformada por tres elementos, explicados a su vez tal como se muestra seguidamente:
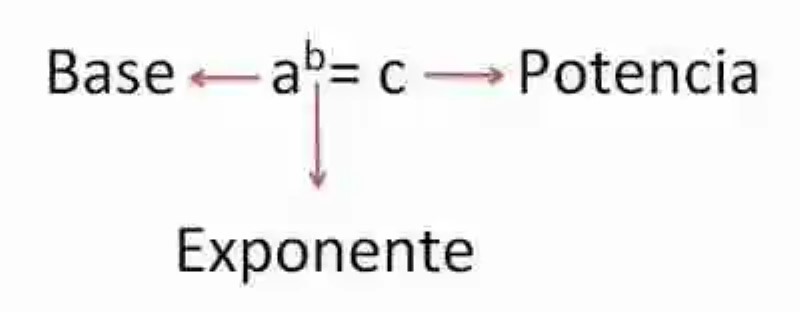
- Base: en primer lugar, la Base será entendida como el elemento numérico destinado a multiplicarse por sí mismo, todas las veces que le dicte el segundo número que participa de la operación.
- Exponente: por su parte, el Exponente será el número que le indique a la base cuántas veces deberá multiplicarse por sí misma.
- Potencia: por último, la Potencia es interpretada como el resultado final de la operación, es decir, el producto que se obtiene al multiplicar la base todas las veces que señala el exponente.
Fracciones
Así también, será conveniente tomar un momento para reflexionar sobre la noción de Fracciones, las cuales son entendidas como aquellas expresiones matemáticas, a través de las cuales se da cuenta de números racionales o fraccionarios, es decir, que las fracciones se usan siempre para representar cantidades no exactas o no enteras. Igualmente, la disciplina matemática ha señalado que las fracciones se encuentran conformadas por dos elementos, explicados así:
- Numerador: por un lado, el Numerador constituirá la parte superior de la fracción. Su misión será señalar cuántas partes del todo se ha tomado o son representadas por esta expresión.
- Denominador: en segunda instancia, el Denominador será el elemento que ocupe la parte inferior de la fracción, teniendo la tarea de indicar en cuántas partes se encuentra dividido el todo.
Potencias de base racional
Finalmente, será preciso también aproximarse a la definición de Potencias de base racional, las cuales han sido explicadas de forma general por las matemáticas como un tipo de operación de potenciación en donde la base está constituida por un número racional o fracción. Al igual que sucede en las fracciones de base entera, la solución de esta operación se conseguirá a través de la multiplicación de la base por sí misma las veces que señale el exponente:
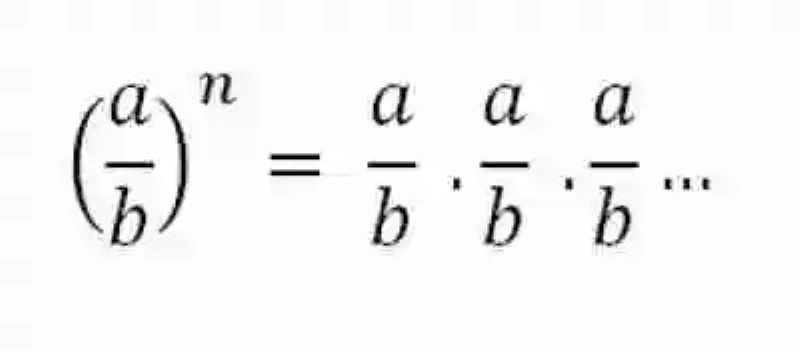
No obstante, la mayoría de las fuentes se inclina por resolver estas operaciones a través de la fórmula general para potencias de fracciones, la cual indica que lo mejor en estos casos es elevar por separado cada elemento de la fracción al exponente indicado, procedimiento que podrá representarse matemáticamente tal como se ve a continuación:

Producto de potencias de fracciones de la misma base
Una vez se han revisado estas definiciones, quizás ciertamente resulte mucho más sencillo abordar una explicación sobre la forma en que debe ser resuelta toda multiplicación de potencias de base racional en donde se determine que todas cuentan con la misma base, es decir, con la misma fracción como base.
En este tipo de casos, existe una ley matemática que indica –que al igual que sucede con las potencias de base entera- se deberá optar por asumir una sola base y proceder a sumar cada uno de los exponentes presentados. Esta propiedad podrá expresarse matemáticamente de la siguiente manera:

Ejemplo
Empero, quizás la mejor forma de completar una explicación sobre la forma adecuada en que debe ser resuelta una operación de este tipo sea la exposición de un ejemplo concreto, que permita ver en la práctica cómo se aplica la propiedad matemática que dicta cómo proceder en el caso de que los factores de una multiplicación de potencias de fracciones cuenten con bases iguales. A continuación, el siguiente ejercicio:
Resolver la siguiente multiplicación de potencias de fracciones:
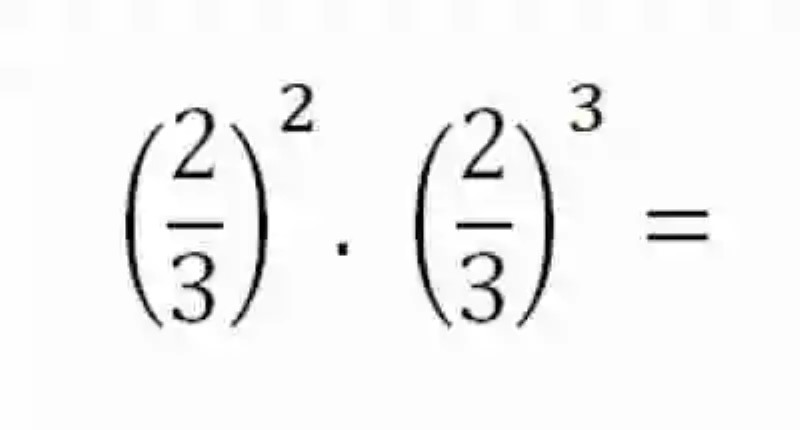
Para dar cumplimiento al postulado, se deberá verificar que en efecto ambas potencias cuentan con la misma base, por lo que entonces se procederá a asumir una sola de ellas, y a sumar sus exponentes:
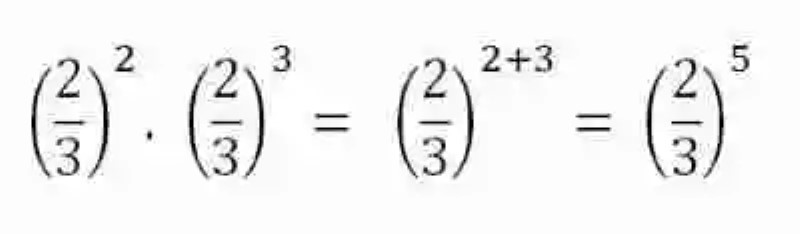
Hecho esto, se deberá continuar entonces con dar solución a la operación, para lo que se aplicará la fórmula general de potencias de fracciones, elevando cada elemento de la expresión al exponente señalado:

Llegado al resultado de la potencia, si se determinara que no se puede seguir simplificando, entonces se asumirá este producto como la solución final de la operación.
Imagen: pixabay.com
El pensante.com (febrero 15, 2018). Producto de potencias racionales de igual base. Recuperado de https://elpensante.com/producto-de-potencias-racionales-de-igual-base/