
Tabla de contenido
Antes de abordar una explicación sobre el Producto de las soluciones de ecuaciones de segundo grado completas, se revisarán algunas definiciones, que de seguro permitirán entender este procedimiento, que además es señalado como una propiedad matemática de este tipo de expresiones, dentro de su justo contexto.
Definiciones fundamentales
En consecuencia, también se optará por delimitar esta revisión teórica a cuatro nociones específicas: Igualdades, Ecuaciones, Ecuaciones de segundo grado y Fórmula general para ecuaciones de segundo grado completas, por encontrarse directamente relacionadas con la propiedad matemática que se estudiará posteriormente. A continuación, cada una de estas definiciones:
Igualdades
De esta forma, se comenzará por decir que las Igualdades pueden ser entendidas entonces como un tipo de relación matemática, la cual se establece entre dos elementos o términos, que resultan idénticos en cuanto a su valor total. Así mismo, tal como señalan las distintas fuentes, el signo matemático que permite expresar esta relación será el signo e igual (=).
Por otro lado, las Matemáticas también indican que en las Igualdades se reconocen dos distintos términos, los cuales básicamente han sido explicados de la siguiente forma:
- Primer término: se encuentra conformado por el elemento o conjunto de elementos que se disponen de forma anterior al signo igual.
- Segundo término: por su parte, el segundo término de la igualdad se encontrará conformado entonces por los elementos que existan después del signo usado para expresar esta relación.
Además, la disciplina matemática indica que en cuanto a las igualdades se puede hablar de dos tipos específicos:
- Igualdades numéricas: las cuales ocurren entre elementos exclusivamente numéricos.
- Igualdades literales: entendidas como aquellas que ocurren entre términos que se encuentran conformados tanto por números como por literales.
Ecuaciones
En segundo lugar, se lanzarán luces sobre el concepto de Ecuaciones, las cuales han sido explicadas de forma general como todo tipo de igualdad literal en la que el elemento literal constituye una incógnita, que debe despejarse, pero que tiene la oportunidad de contar tan solo con una respuesta, pues esta es la única que permite que la igualdad se cumpla. Un ejemplo de este tipo de relaciones será la siguiente:
Suponiendo que se cuente con la siguiente igualdad: 3 + x = 8
Se puede optar por sustituir el valor de x por distintas cantidades, a fin de descubrir cuál de ellas sirve para que la igualdad presentada se cumpla:
3 + 2 = 8 → 5 ≠ 8
3 + 3 = 8 → 6 ≠ 8
3 + 9 = 8 → 12 ≠ 8
3 + 5 = 8 → 8 = 8Al hacerlo, se puede encontrar entonces cómo la igualdad sólo se puede cumplir cuando la x es igual a 5. Al tener una sola posible solución entonces se concluye que la igualdad literal es una ecuación. Si por el contrario esta igualdad se cumpliera con cualquier valor, entonces la expresión se asumiría como una Identidad.
Ecuaciones de segundo grado
De igual forma, es necesario señalar la definición de Ecuaciones de segundo grado, las cuales han de ser explicadas como aquellas igualdades literales, en donde el literal, no sólo constituye la incógnita a ser despejada, sino que se encuentra elevado al cuadrado. Si la expresión contara con más literales, el exponente de mayor valor sería el cuadrado. Un ejemplo de la forma reducida que puede tener esta expresión será la siguiente:
ax2 + bx + c = 0
Así también, será necesario señalar cómo las Ecuaciones de segundo grado se encuentran conformadas por dos distintos tipos de componentes:
- Elementos: en primer lugar, se distinguirán los elementos, categoría en donde pueden contarse dos distintos subtipos: los coeficientes a, b y c, los cuales estarán constituidos en todo momento por elementos numéricos; y por otro lado, la incógnita, representada por lo general con la letra x.
- Términos: además de los elementos, en las ecuaciones de segundo grado podrán contarse también tres distintos términos, explicados de la siguiente manera:
- ax2 → término cuadrático, cuya misión es indicar el grado de la ecuación.
- bx → término lineal.
- c → término independiente, denominado así por ser un elemento numérico sin presencia o compañía del elementos literal.
La presencia o ausencia de estos términos origina también dos distintos tipos de ecuaciones de segundo grado, las cuales han sido explicadas de la siguiente manera:
- Ecuaciones incompletas: serán ecuaciones que cuenten con un término cuadrático, pero que pueden presentar la ausencia del término lineal o el término independiente, o incluso de ambos. Esta situación se da porque los coeficientes de estos términos resultan iguales a cero, originando estas distintas ecuaciones de segundo grado:
ax2 + b = 0
ax2 + c = 0
ax2 = 0
- Ecuaciones completas: por su parte, las ecuaciones de segundo grado completas serán aquellas que cuenten con la totalidad de sus términos, situación que vienen dada por presentar coeficientes a, b y c, distintos a cero. En su forma reducida, estas ecuaciones responderán a la siguiente forma:
ax2 + bx + c = 0
Fórmula general para ecuaciones de segundo grado completas
Por último, será necesario pasar revista sobre la definición de Fórmula general, para la solución de ecuaciones de segundo grado. En este orden de ideas, es necesario señalar que las Matemáticas conciben dos distintos métodos para solucionar este tipo de igualdades literales: por un lado, puede aplicarse el método del cuadrado perfecto; y por otro, el método de la fórmula general, el cual contará con la siguiente expresión:
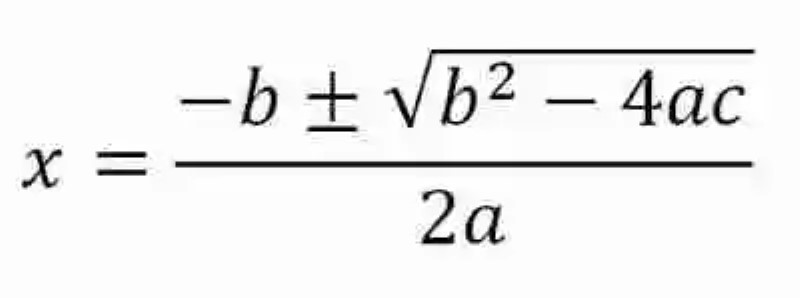
Respecto a esta fórmula, es importante aclarar que las Matemáticas denominan al radicando del radical como Discriminante, atribuyéndole la responsabilidad, según sea de naturaleza positiva, negativa o nula, de indicar cuántas posibles soluciones tiene la ecuación.
Producto de soluciones de ecuaciones de segundo grado
Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse a una explicación sobre el Producto de las soluciones de ecuaciones de segundo grado, operación esta que es entendida entonces como una propiedad matemática de este tipo de igualdades literales, la cual dicta que siempre y en todo momento el producto de las soluciones de una ecuación de segundo grado es igual al término independiente de esta ecuación entre el coeficiente del término cuadrático, o en su defecto al valor que tendría el cociente entre estos elementos. Esta propiedad puede expresarse de la siguiente forma:
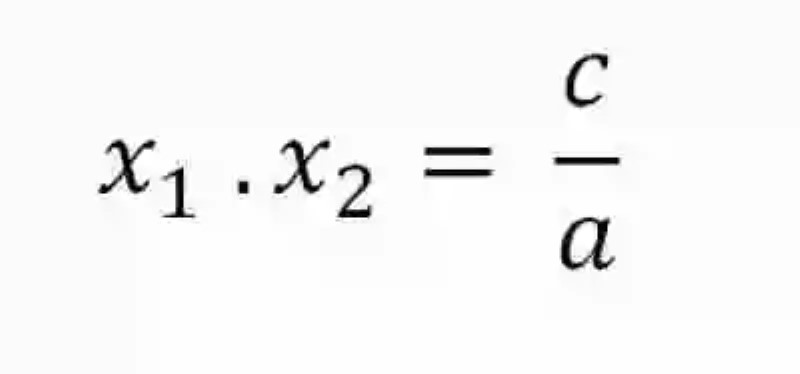
Imagen: pixabay.com
El pensante.com (febrero 18, 2019). Producto de soluciones de ecuaciones de segundo grado. Recuperado de https://elpensante.com/producto-de-soluciones-de-ecuaciones-de-segundo-grado/