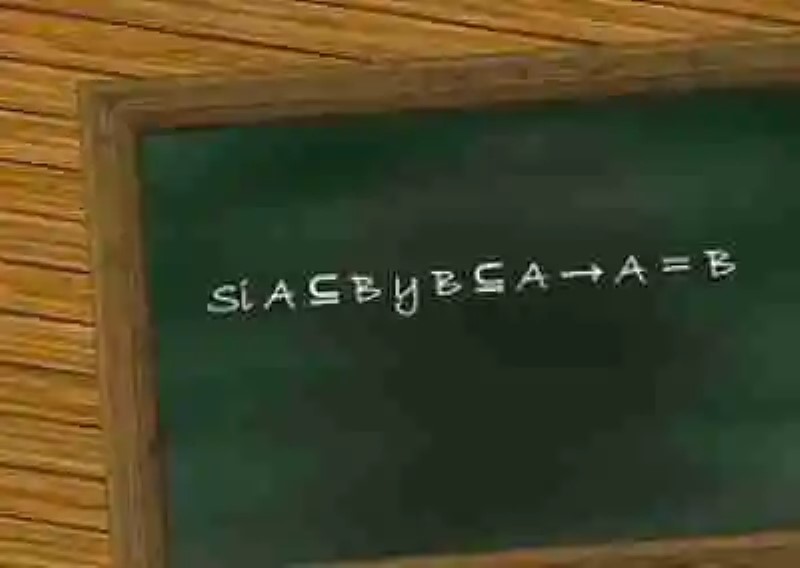
Es probable que, previo a abordar la definición y demás aspectos de la Propiedad Antisimétrica en el Subconjunto, sea necesario revisar algunas definiciones, que permitirán entender esta Ley matemática dentro de su contexto teórico preciso.
Definiciones fundamentales
En este sentido, quizás resulte pertinente comenzar por la propia definición de Conjunto, a fin de poder tener clara la naturaleza del objeto matemático en base a la cual se da la relación de Subconjunto, concepto este que también deberá ser aclarados, con el propósito de garantizar el entendimiento de cada uno de los términos que entran en juego en la Propiedad Antisimétrica del Subconjunto. A continuación, cada una de las definiciones:
Conjunto
Por consiguiente, se puede comenzar diciendo entonces que el Conjunto ha sido definido por las Matemáticas como una agrupación de elementos, los cuales pueden pensarse como una colección abstracta, debido a que todos ellos coinciden en al menos un elemento en común, de ahí que sean considerados parte de una misma naturaleza. Así mismo, las distintas fuentes teóricas han señalado que los conjuntos se distinguen principalmente por estar conformados y definidos únicamente por sus elementos.
Subconjunto
Igualmente, la disciplina matemática también se ha dado a la tarea de definir al Subconjunto, el cual puede ser entendido como una colección abstracta de elementos, que cuenta con la propiedad de encontrarse comprendida de forma plena y absoluta por otra de mayor tamaño. En otras palabras, el Subconjunto será un conjunto, en donde cada uno de sus elementos podrá encontrarse a su vez como elementos de otro conjunto, por lo que se dice entonces que el Subconjunto forma parte de este. La expresión matemática de este tipo de conjunto será la siguiente:
B ⊆ A
Propiedad antisimétrica del Subconjunto
Teniendo presentes estas definiciones, quizás resulte mucho más sencillo entender cada uno de los términos de la Propiedad Antisimétrica del Subconjunto, la cual puede ser entendida como la Ley matemática que indica que cuando un Conjunto A es identificado como Subconjunto de B, y a la vez el Conjunto B puede señalarse también como subconjunto de A, entonces se concluye que los conjuntos A y B son iguales. En cuanto a la expresión matemática de esta propiedad puede tenerse la siguiente forma:
Si A ⊆ B y B ⊆ A → A = B
Ejemplo de Propiedad Antisimétrica del Subconjunto
No obstante, puede que la forma más eficiente de explicar esta propiedad matemática sea a través de la exposición de un caso concreto, que pueda servirle de ejemplo, tal como el que se muestra a continuación:
Dado un conjunto A, conformado por nombres de frutas cuyo nombre comience por la letra “m”: A= {Manzana, Mango, Maní, Mandarina, Mangostino} y un conjunto B, en el cual se puedan contar como elementos frutas en general: B= {Mangostino, Mango, Mandarina, Maní, Manzana} comprobar si se cumple la Propiedad Antisimétrica del Subconjunto.
Para cumplir con el postulado, se deberá comenzar por traer a capítulo la forma matemática de esta ley, a fin de comenzar por resolver cada una de las operaciones que ella contempla:
Si A ⊆ B y B ⊆ A → A = B
En tal sentido, se debe comenzar por verificar si realmente A es un subconjunto de B, para lo que se someterán ambas colecciones a una operación de intersección:
A= {Manzana, Mango, Maní, Mandarina, Mangostino}
B= {Mangostino, Mango, Mandarina, Maní, Manzana}A ∩ B=
A ∩ B= {Manzana, Mango, Maní, Mandarina, Mangostino} ∩ {Mangostino, Mango, Mandarina, Maní, Manzana}A ∩ B= {Manzana, Mango, Maní, Mandarina, Mangostino}
Al hacerlo, se obtiene que el resultado de la operación es equivalente al conjunto A, por lo que se asume que efectivamente A es subconjunto de B:
A ⊆ B
Por otro lado, también se deberá comprobar que B sea un subconjunto de A, por lo que entonces se deberá realizar igualmente una operación de intersección, pero en sentido inversa, para comprobar si en efecto, B también es un subconjunto de A:
B= {Mangostino, Mango, Mandarina, Maní, Manzana}
A= {Manzana, Mango, Maní, Mandarina, Mangostino}B ∩ A=
B ∩ A= {Mangostino, Mango, Mandarina, Maní, Manzana} ∩ {Manzana, Mango, Maní, Mandarina, Mangostino}B ∩ A= {Mangostino, Mango, Mandarina, Maní, Manzana}
Cuando se hace, se puede ver entonces cómo este resultado coincide de forma plena con el conjunto B, por lo que entonces se puede decir que B también es un subconjunto de A: B ⊆ A. Obtenida esta conclusión, la única forma –según la Propiedad Antisimétrica de Conjuntos- de que esto sea posible, es decir, que A sea subconjunto de B (A ⊆ B) y B sea subconjunto de A (B ⊆ A.) es que A y B sean iguales, lo cual se comprobará simplemente con haciendo una comparación de sus elementos:
A= {Manzana, Mango, Maní, Mandarina, Mangostino}
B= {Mangostino, Mango, Mandarina, Maní, Manzana}Una vez cumplido con este paso, se puede notar que ambos conjuntos cuentan con los mismos elementos, aun cuando no tengan el mismo orden, lo cual se puede resolver fácilmente, disponiéndolos de igual forma:
A= {Manzana, Mango, Maní, Mandarina, Mangostino}
B= {Manzana, Mango, Maní, Mandarina, Mangostino}Efectivamente, ambos conjuntos son iguales, por lo que se puede decir que se ha comprobado la Propiedad Antisimétrica de conjuntos:
Si A ⊆ B y B ⊆ A → A = B
Imagen: pixabay.com
El pensante.com (julio 27, 2017). Propiedad antisimétrica del Subconjunto. Recuperado de https://elpensante.com/propiedad-antisimetrica-del-subconjunto/