
Tabla de contenido
Quizás lo más conveniente, antes de avanzar en una explicación referente a la Propiedad conmutativa en la multiplicación de fracciones, sea revisar de forma breve algunas definiciones, que permitirán entender esta Ley matemática dentro de su contexto apropiado.
Definiciones fundamentales
En este sentido, puede que lo mejor sea enfocar esta revisión en dos nociones específicas: la primera de ellas, la definición misma de fracción, pues esto permitirá tener presente cuál es la naturaleza de las expresiones matemáticas involucradas en esta propiedad matemática. Así mismo, será prudente lanzar luces sobre el concepto de Multiplicación de fracciones, por ser esta la operación en cuanto a la que se da la Ley conmutativa. A continuación, cada una de estas definiciones:
Fracciones
De esta manera, será importante comenzar a decir que las Fracciones pueden ser entendidas como una de las dos posibles expresiones matemáticas que tienen los números fraccionarios, por lo que entonces estas servirán para representar cantidades no exactas o no enteras. Por otro lado, las Matemáticas también han indicado que las fracciones estarán compuestas por dos elementos, cada uno de ellos descritos a su vez de la siguiente manera:
- Numerador: en primer lugar, se encontrará el numerador, elemento que ocupa la parte superior de la fracción, y cuya principal misión es dar cuenta de la cantidad que se ha tomado respecto al todo.
- Denominador: por su parte, el denominador estará constituido por el número que ocupa la parte inferior de la fracción. Su tarea será señalar por cuántas partes está constituido el todo.
Multiplicación de fracciones
Así mismo, será de gran importancia abordar el concepto de Multiplicación de fracciones, la cual puede ser explicada entonces como una operación matemática por medio de la cual se busca esclarecer o determinar cuál es el resultado de sumar por sí misma una fracción específica, tantas veces como señale una segunda fracción, de ahí que esta operación haya sido interpretada igualmente como una suma abreviada de fracciones.
En cuanto a su forma específica de ser resuelta, las Matemática señalan también que se deberá proceder a multiplicar el número que constituye el numerador de la primera fracción por el numerador de la segunda, para conseguir el numerador del producto, al tiempo en que también se deberán multiplicar los denominadores de las fracciones involucradas en la operación, con el fin de obtener el denominador del producto de la fracción, procedimiento que podrá ser expresado matemáticamente de la siguiente manera:
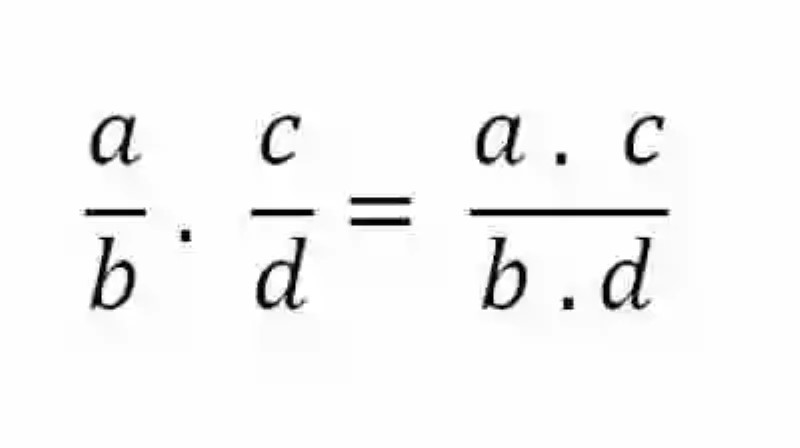
Propiedad conmutativa en la multiplicación de fracciones
Teniendo presente estas definiciones, tal vez ciertamente sea mucho más sencillo entender la explicación que ofrece la Matemática sobre la Propiedad conmutativa presente en esta operación, y que básicamente ha sido descrita como la Ley que señala que siempre y si excepción cuando dos o más fracciones se multipliquen, en realidad estas pueden alterar o variar sus órdenes, puesto que esto no representará ningún cambio en el resultado o producto obtenido. Es decir, que el orden de los factores no altera el producto. Así mismo, esta Propiedad puede ser expresada matemáticamente de la siguiente manera:
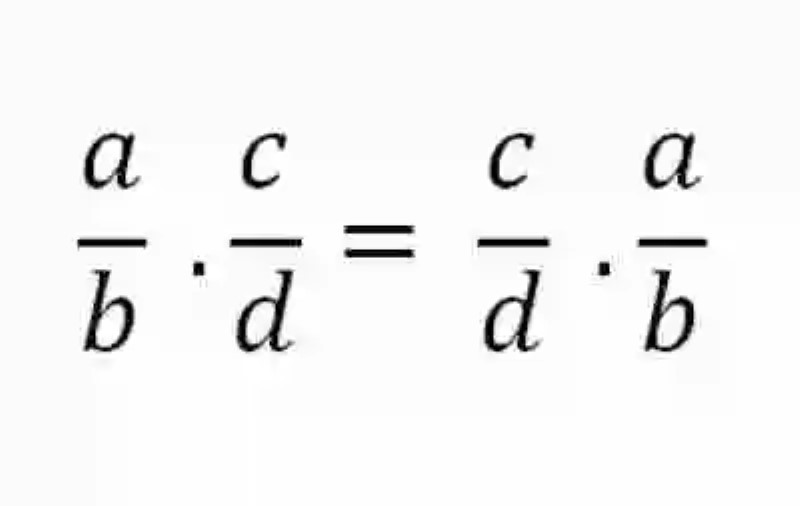
Ejemplo de Propiedad conmutativa en la multiplicación de fracciones
Sin embargo, puede que la mejor forma de completar una explicación sobre la Propiedad conmutativa en la multiplicación de fracciones sea a través de la exposición de un ejemplo concreto, que permita ver en la práctica cómo realmente una vez que los factores cambian su orden no se produce ninguna alteración en el resultado, tal como puede verse a continuación:

Imagen: pixabay.com
El pensante.com (enero 18, 2018). Propiedad conmutativa en la multiplicación de fracciones. Recuperado de https://elpensante.com/propiedad-conmutativa-en-la-multiplicacion-de-fracciones/