Propiedad conmutativa en la suma de fracciones

Definiciones fundamentales

En este sentido, quizás también sea prudente delimitar esta revisión a dos nociones específicas: en primer lugar será pertinente abordar el concepto de fracción, puesto que este será necesario a la hora de entender la expresión matemática involucrada en la operación de suma que da pie a esta propiedad matemática, cuya definición también deberá será traída a capítulo. A continuación, cada una de ellas:

La fracción

De esta manera, se comenzará por decir entonces que las Matemáticas señalan la Fracción como una de las dos expresiones con las que puede contar un número fraccionario, explicado a su vez como el elemento numérico por medio del cual se representa un número no entero o no exacto.

Así mismo, esta disciplina indica que la fracción se presentará como una división entre dos números enteros, los cuales se disponen uno sobre otro. El elemento numérico que ocupa la posición superior recibirá el nombre de Numerador, y se encargará de señalar cuál parte del todo representa la fracción. Por su parte, el número ubicado en la parte inferior, se llamará Denominador, y tendrá como objetivo dar cuenta de cuál es el todo del que se ha tomado una parte. Algunos ejemplos de fracciones serán los siguientes:

Suma de fracciones

En cuanto a la Suma de fracciones esta será entendida como una operación matemática, en la cual se trata de encontrar el total que arrojaría la adicción de los respectivos valores de dos o más fracciones, que ejercerían el papel de sumandos. Sin embargo, las Matemáticas también señalan que la forma de resolver este tipo de operación dependerá básicamente de si las fracciones coinciden o no en cuanto a su denominador, teniendo entonces estas dos posibilidades:

• Fracciones con igual denominador: en caso de que las fracciones involucradas en una suma cuenten con iguales denominadores, entonces la operación de suma deberá resolverse simplemente a través de la suma de los valores con los que cuentan los numeradores.
• Fracciones con diferente denominador: por el contrario, si las fracciones que fungen como sumandos no cuentan con iguales denominadores, entonces será necesario, antes de avanzar en la suma de fracciones, hallar el común denominador, para que una vez calculado, se proceda entonces a la suma de los respectivos numeradores, obtenidos en las operaciones realizadas para la determinación de este común denominador.

Propiedad conmutativa en la suma de fracciones

Teniendo presente estas definiciones, quizás entonces sea mucho más sencillo abordar una definición sobre la Propiedad conmutativa presente en esta operación matemática. En este orden de ideas, será necesario decir que como toda operación de suma, la sucedida en fracciones cumple con la Ley conmutativa, la cual indica que siempre y sin ninguna excepción los sumandos de esta operación pueden intercambiar sus respectivos posiciones, puesto que el “orden de los factores no alterará el producto”. Esta propiedad puede expresarse matemáticamente de la siguiente manera:

Ejemplo de Propiedad conmutativa en la suma de fracciones

Sin embargo, puede que todavía sea necesario un ejemplo concreto que permita ver en la práctica cómo realmente siempre que se altere o modifique el orden en la suma de fracciones, se obtendrá iguales resultados. Para esto, se tomará como ejemplo una suma entre fracciones de diferente denominador, a fin de mostrar el caso más complejo, y como independientemente de esto la Propiedad conmutativa se sigue cumpliendo sin excepción, tal como se muestra a continuación:

En la siguiente operación, comprobar la propiedad conmutativa:

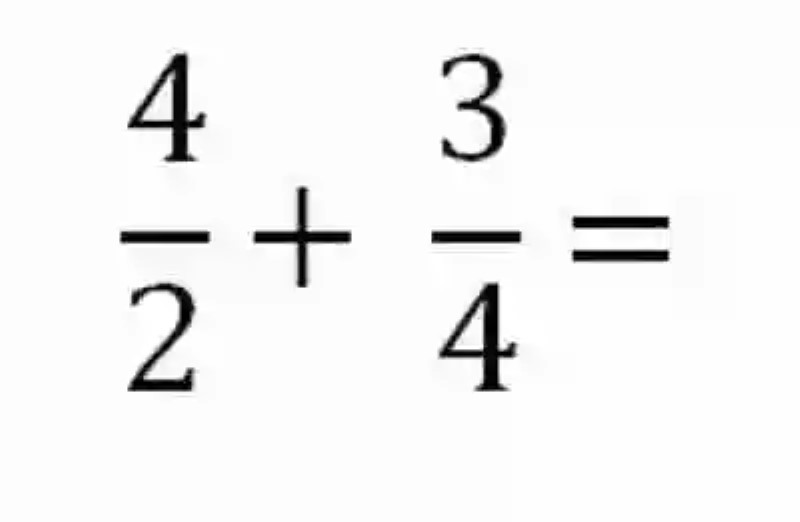
Para cumplir con lo promulgado por este planteamiento, será necesario comenzar por resolver la operación en el orden expuesto. Tomando en cuenta que para esto se deberá entonces calcular el denominador común, antes de proceder a la suma:

Teniendo ahora dos fracciones de igual denominador, se podrá resolver la suma, haciendo que los valores del numerador hallen un total:

La fracción resultante podrá simplificarse, por lo que será necesario dividir cada elemento de la expresión entre un común divisor:

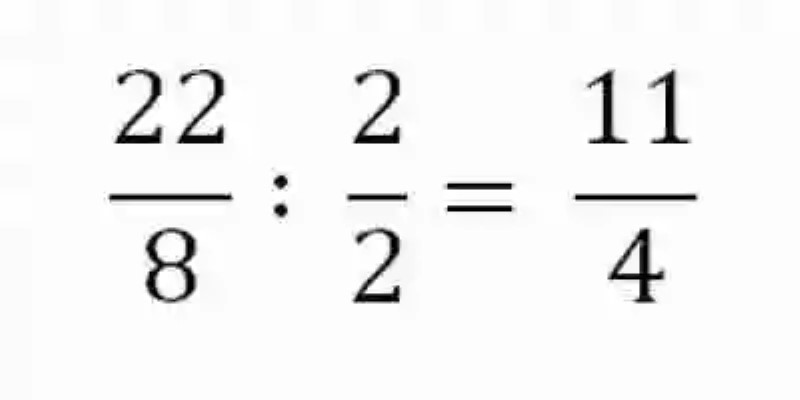
Al llegar a este resultado, no se podrá seguir simplificando, por lo que se tomará como producto final de la operación. Hecho esto, se deberá entonces invertir el orden de los sumandos originales, para comprobar si haciéndolo se obtienen igual resultado en la suma de fracciones:

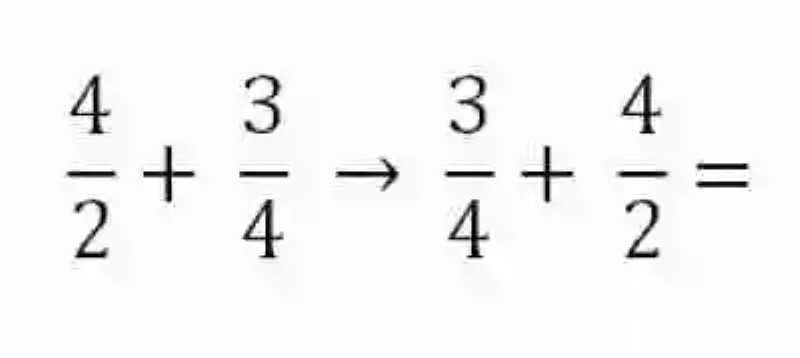
Siendo todavía fracciones de distinto denominador, el primer paso para la solución de esta suma será encontrar el común denominador. Tomando en cuenta que la multiplicación también responde a la ley conmutativa no existe riesgo de que se encuentren resultados distintos:

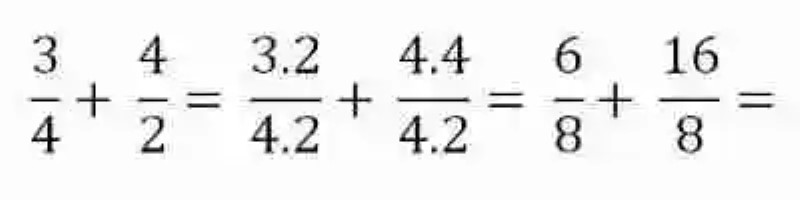
Llegado a este punto, se puede observar que se han obtenido iguales factores luego del cálculo del común denominador. Así mismo, se puede dar continuidad a la operación de suma:

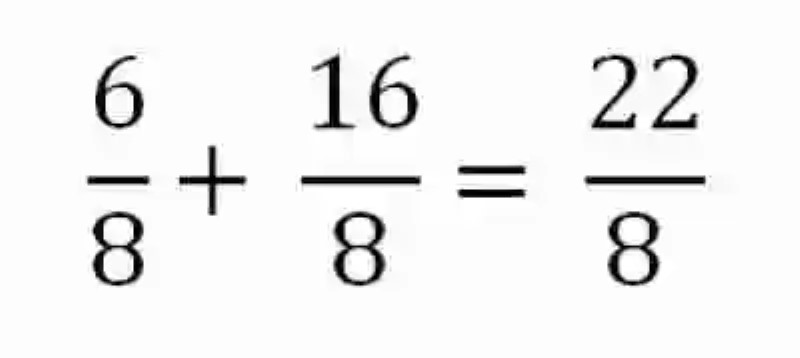
Así mismo, se deberá simplificar el resultado a través de dividir cada término entre un común denominador:

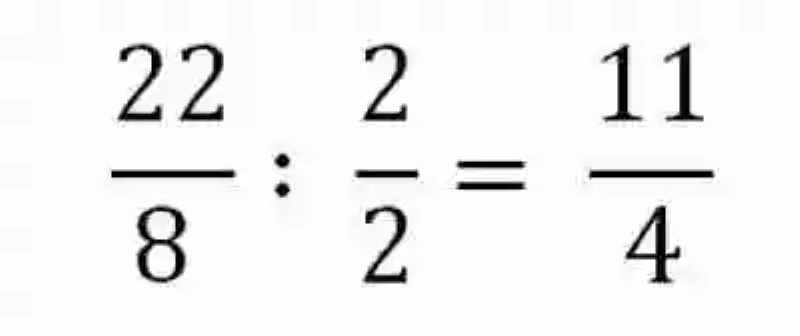
Se ha obtenido iguales resultados, por lo que en este caso se considera comprobada la Propiedad conmutativa en la suma de fracciones.

Imagen: