Propiedad del Elemento inverso en la multiplicación de fracciones

Definiciones fundamentales

En consecuencia, será necesario delimitar esta revisión teórica a dos nociones específicas: la primera de ellas, la definición misma de fracciones, ya que eso puede ayudar a entender la naturaleza de las expresiones involucradas en la operación que da pie a la Propiedad del Elemento inverso. De igual forma, será necesario lanzar luces sobre el concepto de Multiplicación de fracciones por ser esta la operación en base a la cual se da esta ley matemática. A continuación, cada uno de estos conceptos:

Fracciones

De esta manera, se comenzará por decir que las Matemáticas han señalado las fracciones como una de las dos posibles expresiones con las que se puede dar cuenta de un número fraccionario, lo que convierte entonces a las fracciones en representaciones de números fraccionarios, es decir, de cantidades no exactas o no enteras.

Así mismo, la disciplina matemática señala que las fracciones podrán ser consideradas como expresiones conformadas por dos elementos: en primer lugar, se encontrará el numerador, el cual constituirá el elemento que se disponga en la parte superior de la fracción, señalando cuál es la parte del todo que representa la fracción; por otro lado, en la fracción también se encontrará el denominador, el cual estará conformado por el número que se encuentra en la parte inferior de la expresión, al tiempo que su misión será señalar en cuántas partes se divide el todo.

Multiplicación de fracción

Siguiendo con la revisión de conceptos, será también necesario detenerse en la noción de Multiplicación de fracciones, la cual ha sido explicada de forma general por las Matemáticas como una operación, destinada a determinar cuál es el producto que puede obtenerse en base a la multiplicación de dos o más fracciones, o lo que es igual: obtener le total de la suma de una fracción por sí misma tantas veces como señale una segunda fracción, puesto que la Multiplicación no es otra cosa que una suma abreviada.

En relación a la forma correcta en que esta operación debe ser resuelta, los distintos autores coinciden en señalar igualmente que se deberá obtener primero el producto de la multiplicación de todos los elementos que fungen como numerador, y cuyo resultado será entendido como el numerador de la expresión. Así mismo, los denominadores podrán ser multiplicados entre sí, a fin de obtener el denominador del resultado final. Este procedimiento podrá ser expresado matemáticamente de la siguiente forma:

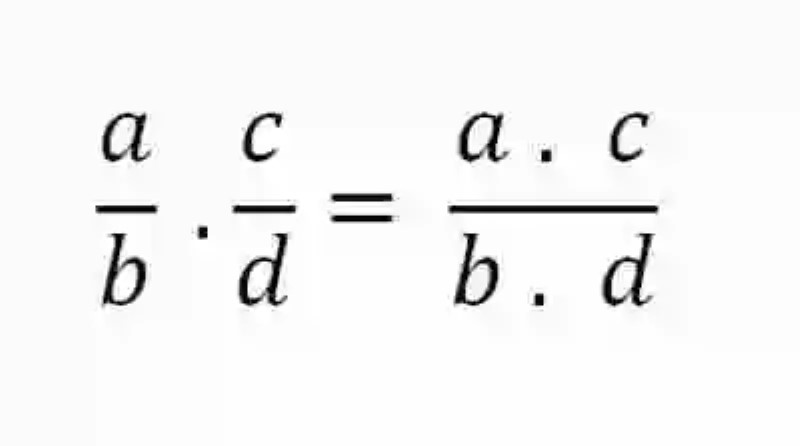
Propiedad del elemento inverso en la Multiplicación de fracciones

Una vez que se han tenido en cuenta estas definiciones, quizás entonces ciertamente sea mucho más sencillo adentrarse en el concepto de la Propiedad del Elemento inverso, la cual es vista por las Matemática como una Ley que señala que siempre y en todo caso que una fracción establezca una operación de multiplicación con su inverso, el resultado o producto será equivalente a la unidad.

Así también, es necesario acotar que el inverso de una fracción será entendido como la misma fracción pero con sus elementos –numerador y denominador- invertidos. Esta propiedad matemática podrá ser expresada matemáticamente de la siguiente manera:

Ejemplos de la Propiedad del Elemento inverso en la multiplicación de fracciones

Sin embargo, puede que todavía sea necesario, antes de concluir con la explicación de esta Ley matemática, exponer algunos ejemplos que permitan ver de forma práctica el cómo y el por qué siempre que una fracción se multiplique con su inverso arrojará como producto la unidad, tal como puede verse a continuación:

Imagen: pixabay.com