
Previo a abordar una explicación sobre la Propiedad del elemento inverso, inherente a la Multiplicación, quizás sea conveniente revisar de forma breve la definición de esta operación, en pro de entender esta ley dentro de su contexto matemático.
La Multiplicación
De esta forma, lo primero que habrá que resaltar de la Multiplicación –en base a lo señalado por las diferentes fuentes- es que puede ser entendida como una de las operaciones aritméticas básicas. Así mismo, será descrita como una operación por medio de la cual un número determinado procede a sumarse a sí mismo tantas veces como indique un segundo número, con el propósito de obtener el total de dicha operación, de ahí que la Multiplicación sea también vista como una suma abreviada. Empero, tal vez la forma más precisa de explicar esta operación sea recurrir a un ejemplo gráfico, tal como el que se muestra seguidamente:
Suponiendo que se cuente con un grupo de 2 cuadrados □□, y se quiera multiplicar esta cantidad por 5, se deberá proceder entonces a sumar estos 2 cuadrados, a sí mismos, un total de 5 veces:
► Ejemplos de identidades de Cauchy Antes de abordar una exposición de algunos e...► ¿En qué consiste la potenciación? La potenciación puede ser definida como la o...► Ángulo recto Quizás lo más recomendable, previo a abordar...5 x 2= □□□□□ x □□→ □□ + □□ + □□ + □□ + □□= □□□□□□□□
Al hacerlo, se obtendrá un total de 10 cuadrados, lo que llevará a concluir entonces que 5×2= 10.
Elementos de la Multiplicación
Por otro lado, las distintas fuentes teóricas también señalan como un punto importante de la definición de las Matemáticas, que esta operación está constituida por cuatro elementos, cada uno de los cuales pueden ser descritos a su vez de la siguiente manera:
- Factores: con este nombre serán identificados cada uno de los números que participan en la operación, tanto aquel que se sumará a sí mismo, como el que indicará cuántas veces deberá realizarse dicha operación.
- Productos intermedios: por su parte, los productos intermedios serán solo generados cuando los números involucrados en la operación sean de más de una cifra. Así mismo, serán considerados como el resultado de la multiplicación de cada número del segundo factor por cada número del primero. Estos productos intermedios serán resultados parciales de la multiplicación, y deberán ser sumados para obtener el resultado global de esta operación.
- Producto: bien si se ha obtenido en base a la suma de los productos intermedios, o de forma directa, el producto será interpretado como el resultado final de la multiplicación.
- Signo: por último el signo cumplirá con la misión de indicar que entre los números involucrados se realiza una operación de multiplicación. En el caso de esta operación, el signo usado recibe el nombre de “por”, y es representado por el signo x, aunque también puede serlo por el signo del punto (.).
Propiedad del Elemento inverso en la Multiplicación
Al igual que todas las operaciones matemáticas, la Multiplicación responde a una serie de leyes matemáticas, las cuales orientan el comportamiento o relaciones por las cuales debe manejarse cada uno de sus elementos, o incluso la propia operación. Un ejemplo de esto lo constituye la Propiedad sobre el Elemento inverso en la Multiplicación, la cual indica que siempre que un número sea multiplicado por su inverso (recordando que el inverso de un número será 1/n) dicha operación dará como resultado la unidad. Esta operación podrá ser expresada matemáticamente de la siguiente forma:
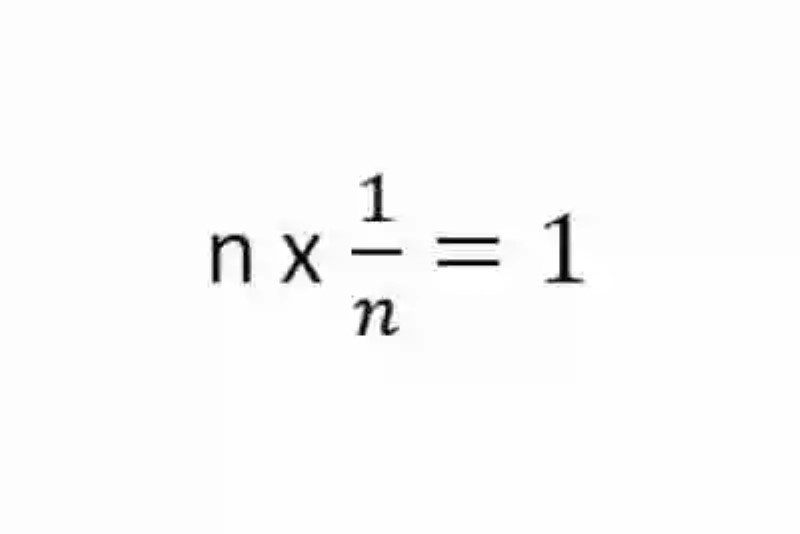
Ejemplo del Elemento inverso en la Multiplicación
No obstante, quizás se necesite de un ejemplo concreto para poder entender la lógica de esta propiedad, es decir cuáles son las operaciones que conducen a ella. A continuación, entonces, un Ejemplo sobre la aplicación de la Propiedad del Elemento inverso en la Multiplicación:

Imagen: pixabay.com
El pensante.com (septiembre 30, 2017). Propiedad del Elemento inverso en la Multiplicación. Recuperado de https://elpensante.com/propiedad-del-elemento-inverso-en-la-multiplicacion/