
Tabla de contenido
Quizás lo más conveniente, previo a abordar una explicación referente al Elemento neutro para la suma de fracciones, sea revisar algunas definiciones, que permitirán entender esta Ley matemática en su contexto preciso.
Definiciones fundamentales
En este sentido, puede que sea prudente también centrar esta revisión teórica en dos nociones básicas: la primera de ellas, el concepto mismo de Fracciones, a fin de tener presente la naturaleza de la expresión matemática o tipo de número en base al cual se establece tanto la operación de suma –cuya definición será la segunda a abordar- como la propia Ley del Elemento neutro. A continuación, cada uno de estos conceptos:
Las fracciones
Por consiguiente, se comenzará por decir que las fracciones son una de las dos formas de representación con las que cuentan los números racionales, y que se encuentra constituida por la división sostenida entre dos números enteros. Así también, las Matemáticas consideran importantes reparar en los elementos que conforman la fracción, y que han sido definidos a su vez de la siguiente manera:
- Numerador: es el elemento que se encuentra en la parte superior. Tiene la misión de señalar cuántas partes del todo representa la fracción.
- Denominador: por su parte, el denominador será el elemento que se encuentra en la parte inferior de la fracción, y cuya misión será señalar cuál es el todo en base al cual se establece la fracción.
Suma de fracciones
En otro orden de ideas, se hará igualmente necesario pasar revista sobre la definición de Suma de fracciones, la cual ha sido entendida como la operación matemática por medio de la cual se busca obtener el total de la combinación de los valores de dos o más fracciones que sirvan como sumandos.
Con respecto a la forma correcta de resolver este tipo de operaciones, las Matemáticas distinguen al menos tres distintos casos:
- Si las fracciones cuentan con igual denominador: en este tipo de suma de fracciones, bastará simplemente con sumar el valor de los numeradores, dejando el mismo denominador.
- Si las fracciones cuentan con distinto denominador: por el contrario, si las fracciones que participan de la suma no son homogéneas, es decir, no cuentan con iguales denominadores, será necesario comenzar la operación calculando el denominador común, a fin de hacer que las fracciones coincidan en cuanto a sus denominadores, y entonces sí puedan proseguir con la suma de sus numeradores.
Propiedad del Elemento neutro para la suma de fracciones
Teniendo presente estas definiciones, es probable que ciertamente sea mucho más sencillo aproximarse a una definición de la propiedad matemática del Elemento neutro para la suma de fracciones, la cual básicamente podrá ser descrita como la Ley que indica que en esta operación matemática, toda vez y sin ninguna excepción, que una fracción se sume con cero, el resultado será la propia fracción. De esta manera, se infiere igualmente que el Elemento neutro en la suma de fracciones será siempre el cero. Esta propiedad puede ser expresada matemáticamente de la siguiente forma:
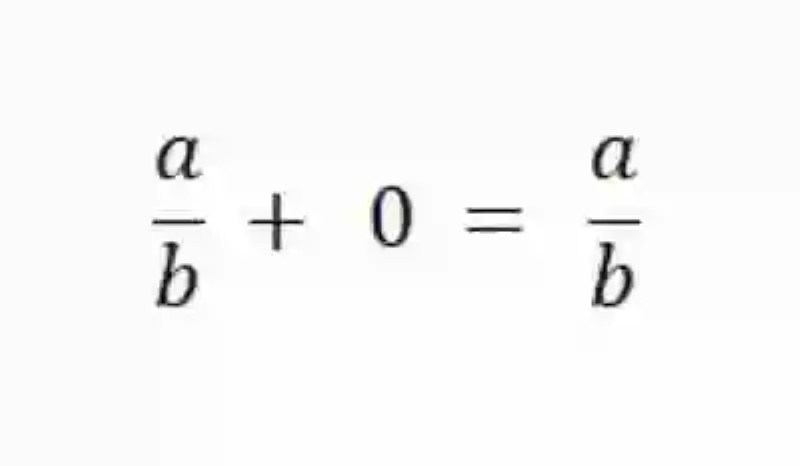
Ejemplos del Elemento neutro en la suma de fracciones
Sin embargo, puede que todavía sea necesario exponer un ejemplo concreto, que permita ver de forma práctica cómo se cumple esta propiedad matemática, es decir, cómo cada vez que una fracción suma o combina su valor con el cero, el resultado es la misma suma, sin que se produzca ningún tipo de alteración en ella, tal como puede verse a continuación:

Imagen: pixabay.com
El pensante.com (diciembre 20, 2017). Propiedad del elemento neutro en la suma de fracciones. Recuperado de https://elpensante.com/propiedad-del-elemento-neutro-en-la-suma-de-fracciones/