
Es probable que la mejor forma de aproximarse a una explicación sobre la Propiedad interna, inherente a la División de fracciones, sea comenzar por la revisión de algunos conceptos, que permitirán entender esta ley matemática en su contexto preciso.
Definiciones fundamentales
En este sentido, puede que también resulte prudente delimitar esta revisión teórica a dos nociones específicas: la primera de ellas, la de la propia fracción, a fin de tener presente la naturaleza de la expresión matemática involucrada en la operación que da lugar a la Propiedad interna, es decir, la División de fracciones, cuyo concepto también deberá ser tomado en cuenta. A continuación, cada uno de ellos:
Fracciones
De esta manera, se comenzará por decir que las Fracciones han sido explicadas por las Matemáticas como una de las dos posibles expresiones con las que cuentan los números fraccionarios, de ahí que se entienda entonces a las fracciones como la representación de cantidades fraccionarias o no exactas.
Por otro lado, esta disciplina también ha indicado que la Fracción estará siempre y sin excepción conformada por dos elementos, cada uno de los cuales ha sido definido a su vez de la siguiente manera:
- Numerador: en primer lugar, se encontrará el Numerador, el cual es el elemento numérico destinado a encontrarse en la parte superior de la expresión, y que cuenta con la tarea de señalar cuáles son las partes del todo de las que da cuenta la fracción.
- Denominador: en segunda instancia, estará el Denominador, elemento de la fracción que ocupa la parte inferior de esta, y que tiene como misión indicar en cuántas partes se encuentra dividido el todo, del cual el numerador señala algunas partes.
División de fracciones
Así mismo, será menester tomar un momento para revisar el concepto que dan las Matemáticas sobre la División de fracciones, las cuales por su parte serán entendidas como un tipo de operación por medio del cual se busca calcular cuál es el cociente obtenido al dividir una fracción entre otra, o lo que es igual: tratar de determinar cuántas veces cabe una fracción específica en otro.
En cuanto a la forma indicada de resolver este tipo de operaciones, las Matemáticas indican que deberá aplicarse el método de la multiplicación cruzada, multiplicando entonces el numerador de la primera fracción por el de la segunda, así también como el denominador de la primera fracción por el numerador de la expresión con la cual se encuentra dividiéndose. El resultado, de ser posible, deberá ser simplificado. Esta operación matemática podrá ser expresada de la siguiente forma:
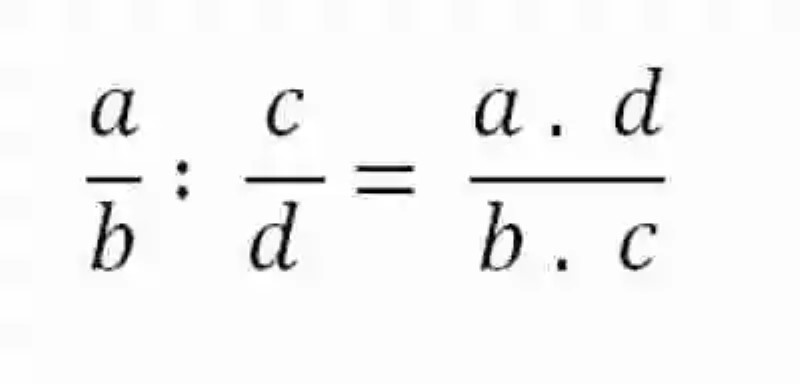
Propiedad interna en la División de fracciones
Teniendo presente cada una de estas definiciones, puede entonces que ciertamente resulte mucho más sencillo abordar una explicación sobre la Propiedad interna presente en la División de fracciones, la cual básicamente estipula que siempre -y sin excepción- que se realice una operación de este tipo, es decir, una División entre dos fracciones, el resultado será igualmente una fracción.
Por ende, esta Ley recibe el nombre de Propiedad interna pues apunta a que los resultados o cocientes obtenidos al solucionar la operación planteada, sea cual fuese, pertenecerá o podrá considerarse dentro de los números fraccionarios, y específicamente dentro de las fracciones.
Ejemplos de la Propiedad interna en la División de fracciones
Sin embargo, puede que la forma más eficiente de cerrar una explicación sobre la Propiedad interna de la División de fracciones sea exponer algunos ejemplos, que permitan ver de forma práctica cómo se cumple esta Ley, tal como puede verse seguidamente:

Imagen: pixabay.com
El pensante.com (enero 31, 2018). Propiedad interna en la División de fracciones. Recuperado de https://elpensante.com/propiedad-interna-en-la-division-de-fracciones/