Propiedad no conmutativa en la resta de fracciones

Definiciones fundamentales

En este sentido, quizás también sea pertinente delimitar esta revisión teórica a dos nociones específicas: la primera de ellas, la propia definición de Fracciones, pues esto permitirá tener presenta la naturaleza de las expresiones en base a las cuales se establece la operación de Resta de fracciones, cuya definición también se traerá a capítulo, por ser el procedimiento matemático en donde tiene lugar la Propiedad no conmutativa. A continuación, cada uno de estas definiciones:

Las fracciones

De esta manera, se comenzará por decir entonces que las fracciones son entendidas por las Matemáticas como una de las dos expresiones que pueden tener  los números fraccionarios, por lo que entonces se asume que la fracción da cuenta de una cantidad no exacta o no entera, de ahí su nombre, puesto que representa una parte o fracción de la cantidad.

Así mismo, la disciplina matemática ha indicado que la fracción se encontrará constituida como una división sostenida entre dos números enteros, cada uno de los cuales ocupan su propia posición, y cumple con su propia tarea, tal como puede verse seguidamente:

• Numerador: por un lado, las Matemáticas indican que el numerador corresponderá al número que ocupe la parte superior de la fracción. Este número tienen como misión el señalar cuál es la parte del todo, que representa la fracción, de la que este numerador hace parte.
• Denominador: por el contrario, el número que se encuentre ocupando la parte inferior de la fracción será entendido entonces como el denominador, el cual cumplirá con la función de señalar en cuántas partes se encuentra dividido el todo.

Resta de fracciones

En otro orden de ideas, también será necesario lanzar luces sobre la definición de Resta de fracciones, la cual será explicada por las Matemáticas como la operación que ocurre cuando una resta, que ejerce las veces de minuendo, suprime en ella la cantidad exacta que le indica una segunda fracción, que se explica como sustraendo, a fin de generar un resultado, que es visto como la diferencia.

No obstante, es importante señalar que las Matemáticas también indican que no existe un solo método para resolver una Resta de fracciones, sino que el método que se aplique dependerá directamente de las relaciones de homogeneidad o heterogeneidad entre las distintas fracciones, teniendo entonces dos casos precisos:

• Si las fracciones son de igual denominador: en caso de que las fracciones que participan de la resta cuenten con igual denominador, es decir, sean homogéneas, la solución a la operación se encontrará asumiendo un solo denominador, y restando los valores de los numeradores.
• Si las fracciones son de diferente denominador: empero, también puede suceder que las fracciones no coincidan en cuanto a sus numeradores o denominadores, lo cual ameritará la necesidad de emprender operaciones que permitan homogeneizar las fracciones, para lo que se aplicará la multiplicación cruzada de numeradores por denominadores, al tiempo que el denominador común se obtendrá multiplicando los valores de los numeradores de cada fracción, tal como se ve a continuación:

Propiedad no conmutativa en la Resta de fracciones

Teniendo presente estas definiciones, quizás ciertamente sea mucho más sencillo abordar una explicación sobre una de las propiedades que se pueden encontrar en la Resta de fracciones: la propiedad no conmutativa. Al respecto, las Matemáticas han señalado que en esta operación tiene lugar esta ley matemática que indica que en la Resta de fracciones toda modificación que se haga en relación al orden de los elementos, es decir, de las fracciones, implicarán cambios directos en la diferencia obtenida, puesto que “el orden de los factores sí altera el producto”, situación que puede ser expresada matemáticamente de la siguiente manera:

Ejemplo de Propiedad no conmutativa en la Resta de fracciones

Empero puede que todavía se necesite un ejemplo concreto que demuestre por qué toda vez que en una operación de resta se inviertan o alteren los lugares de las fracciones, se producirán cambios en el resultado, tal como puede verse a continuación:

Comprobar la Propiedad no conmutativa en la siguiente Resta de fracciones:

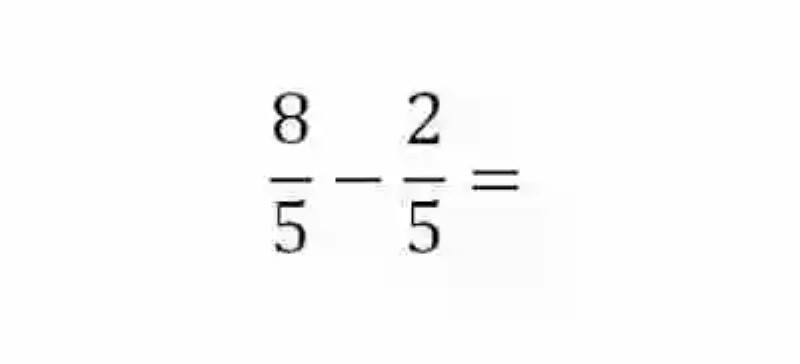
A fin de cumplir con lo que ha señalado el postulado de este ejercicio, será necesario resolver esta resta en los dos órdenes posibles:

Primer orden:

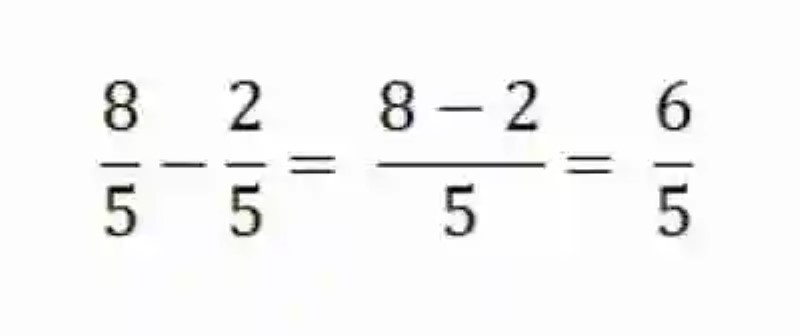
Segundo orden:

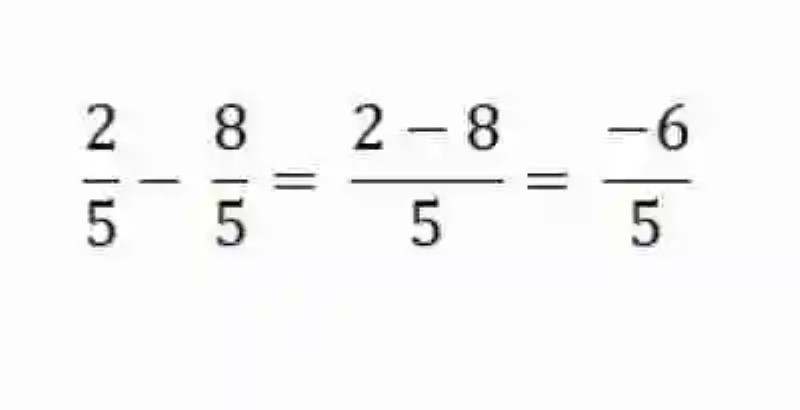
Por ende, al obtenerse resultados diferentes, los cuales incluso arrojan como resultado fracciones inversas, se considera entonces que se ha comprobado la Propiedad no conmutativa en la resta de fracciones, puesto que al variar el orden de sus factores, se obtienen resultados totalmente distintos. Esta relación, o propiedad matemática, en este caso específico, podrá ser expresada entonces de la siguiente manera:

En consecuencia, en una Resta de fracciones no se podrá cambiar el orden de los factores sin que esto conduzca a una alteración en el resultado o diferencia final.

Imagen: pixabay.com