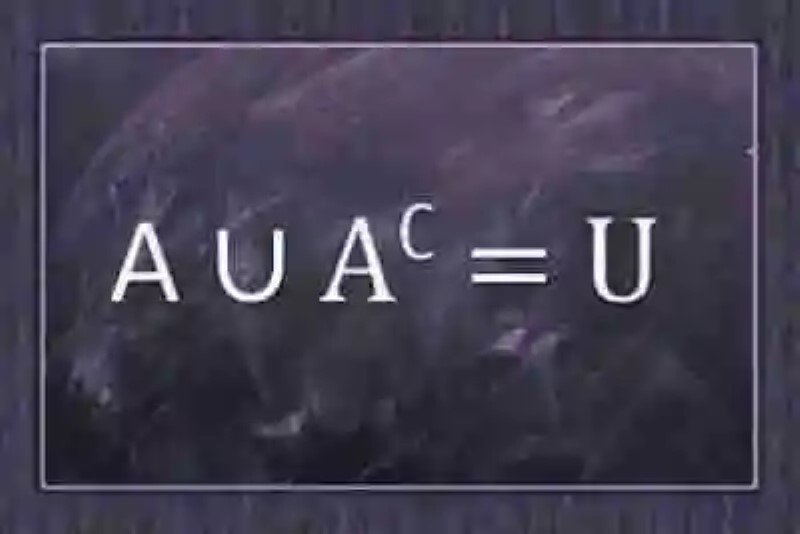
Es probable que antes de avanzar sobre la explicación de la Ley matemática que opera en el momento en que un conjunto determinado establece una operación de Unión con su propio complementario, sea necesario revisar algunas definiciones, indispensables para entender esta propiedad en su contexto adecuado.
Definiciones fundamentales
En este sentido, puede que resulte conveniente revisar entonces algunos conceptos básicos, entre los cuales se encuentran la del propio conjunto, así también como las definiciones de Conjunto Universal y de Conjunto complementario, pues teniéndolas presentes será mucho más sencillo aproximarse a esta Ley matemática entendiendo la terminología, operaciones y situaciones que ella plantea. A continuación, cada uno de estos conceptos:
Conjunto
En primer lugar, es importante referir que la mayoría de fuentes matemáticas describen al Conjunto como una colección abstracta de elementos, los cuales a su vez cuentan con la característica primordial de tener un rasgo en común, de ahí que puedan ser pensados como una agrupación o conjunto. Así mismo, las Matemáticas han señalado que algunas de las características que pueden encontrarse en el Conjunto es que éste está constituido por los elementos, los cuales a su vez cumplen con la función de definirlos de forma única.
Conjunto complementario
Por su parte, el Conjunto complementario es considerado por el Álgebra como un tipo de conjunto, en donde se pueden contar como elementos a todos aquellos elementos que no se encuentran en un conjunto determinado, usando como paradigma al Conjunto Universal. De esta forma, el Conjunto complementario necesita dos parámetros para conocerse, en primer lugar el Conjunto al cual complementa, así también como el Conjunto Universal en donde se encuentra el total de conjuntos que los conforman a los dos. Sabiendo esto, el Conjunto complementario se podrá obtener entonces en base a una operación de Diferencia entre el Conjunto dado y el universal (A∁= U\A).
Conjunto Universal
Así mismo, surge como necesario el definir al Conjunto Universal, el cual dentro del contexto del Conjunto Complementario, puede ser entendido como aquella colección abstracta, en donde pueden contarse de forma plena todos los elementos que hacen parte de una dimensión. Por ende, este conjunto cumple también el papel de ser un Conjunto de referencia, puesto que en él se encuentran contenidos tanto los elementos del Conjunto dado como del Conjunto Complementario.
Unión de un conjunto y su complementario
Teniendo en cuenta estas definiciones, quizás sea mucho más fácil entender la propiedad del Álgebra de Conjuntos, según la cual toda vez que el Conjunto dado establezca una operación de Unión con su Conjunto complementario el resultado no podrá ser otro que el Conjunto Universal. Al reflexionar sobre esta propiedad, se puede ver que resulta lógico que si el Complementario contiene todos los elementos que el conjunto dado no, usando como referente al Conjunto universal, en donde residen de forma plena todos los elementos, pues la Unión del conjunto dado y el complementario dé como resultado un conjunto en donde se encuentren la plenitud de todos los elementos, es decir, que esta operación producirá sin duda alguna al Conjunto Universal:
U= A U A∁
U = │A│+ │A∁│
Ejemplo de la unión de un conjunto y su complementario
Sin embargo, quizás la explicación teórica no sea suficiente para abarcar la explicación de esta propiedad matemática, por lo que no está demás exponer un ejemplo concreto de cómo la suma de la totalidad de los elementos del conjunto y su complemento arroja como resultado el Conjunto universal que ambos tienen como referencia. A continuación, un ejemplo de ello:
Dado un conjunto A, conformado por nombres femeninos que comienzan por la letra “n”: A= {Nadia, Nidia, Nereida, Naira, Noemí} comprobar si ciertamente al unirlo con su complementario se obtiene el Conjunto universal, el cual en este caso está conformado por los siguiente elementos: U= {Natalia, Nataly, Nadia, Nidia, Natasha, Nicole, Naira, Noemí, Nora, Norma}
A fin de dar cumplimiento con la solicitud hecha por este postulado, se deberá proceder en primer lugar a determinar cuál es el conjunto complementario de A, lo cual se hará expresando ambos conjuntos (A y U) y luego sometiéndolos a una operación de Diferencia:
A= {Nadia, Nidia, Nereida, Naira, Noemí}
U= {Natalia, Nataly, Nadia, Nidia, Natasha, Nicole, Naira, Noemí, Nora, Norma}A∁= U\A
A∁= {Natalia, Nataly, Nadia, Nidia, Natasha, Nicole, Naira, Noemí, Nora, Norma} \ {Nadia, Nidia, Nereida, Naira, Noemí}A∁= {Natalia, Nataly, Natasha, Nicole, Nora, Norma}
Obtenido el Conjunto complementario, se deberá entonces someter al Conjunto dado y al complementario a una operación de Unión, a fin de comparar el resultado con el Conjunto Universal, para ver si realmente coinciden o no:
A= {Nadia, Nidia, Nereida, Naira, Noemí}
A∁= {Natalia, Nataly, Natasha, Nicole, Nora, Norma}A ∪ A∁=
A ∪ A∁= {Nadia, Nidia, Nereida, Naira, Noemí} ∪ {Natalia, Nataly, Natasha, Nicole, Nora, Norma}A ∪ A∁= {Nadia, Nidia, Nereida, Naira, Noemí, Natalia, Nataly, Natasha, Nicole, Nora, Norma}
Al comparar el resultado con el Conjunto Universal puede verse cómo pese a no tener el mismo orden de elementos, estos coinciden de forma plena.
A ∪ A∁= {Nadia, Nidia, Nereida, Naira, Noemí, Natalia, Nataly, Natasha, Nicole, Nora, Norma}
U= {Natalia, Nataly, Nadia, Nidia, Natasha, Nicole, Naira, Noemí, Nora, Norma}Por ende se puede concluir entonces que realmente se cumple la propiedad matemática, ya que la operación de Unión de un conjunto con su complementario es equivalente al Conjunto Universal concerniente a los dos conjuntos:
A ∪ A∁= U
Imagen: pixabay.com
El pensante.com (julio 8, 2017). Propiedad sobre la Unión de un Conjunto y su complementario. Recuperado de https://elpensante.com/propiedad-sobre-la-union-de-un-conjunto-y-su-complementario/