Propiedades matemáticas presentes y ausentes en la división de fracciones

Definiciones fundamentales

En este sentido, será necesario también enfocar esta revisión a dos nociones precisas: las fracciones y la división de fracciones, por ser estas respectivamente la expresión y la operación matemática en base a las cuales tienen o no existencia las propiedades que les son atribuidas por esta disciplina. A continuación, cada una de ellas:

Fracciones

De esta manera, se podrá comenzar a decir que las fracciones han sido explicadas por la disciplina matemática como una de las dos posibles formas de expresión con las que cuentan los números fraccionarios, es decir, que las fracciones serán usadas para representar cantidades fraccionarias o no enteras.

Por otro lado, las diferentes fuentes optan por indicar que la fracción es una expresión conformada por dos elementos, cada uno de los cuales han sido descritos de la siguiente forma:

• Numerador: en primer lugar, las Matemáticas mencionan al Numerador, el cual se ubicará siempre y sin excepción en la parte superior de la expresión. Su tarea será señalar cuántas partes del todo se han tomado, o representa la fracción.
• Denominador: con respecto al Denominador, los diversos autores señalan que este ocupará el nivel inferior de la fracción, señalando por su lado en cuántas partes se encuentra dividido el todo, del cual el numerador representa solo una fracción.

División de fracciones

Así mismo, será de gran ayuda pasar revista sobre el concepto de División de fracciones, la cual es vista entonces como una operación matemática, por medio de la cual se busca calcular cuántas veces se encuentra contenida una fracción, que hace las veces de divisor, dentro de otra expresión del mismo tipo, que por su parte funge como dividendo.

En cuanto a la forma correcta en la que debe desarrollarse este tipo de operaciones, a fin de obtener el cociente, las Matemáticas señalan que el mejor método será el de la multiplicación cruzada, en donde el numerador de la primera expresión se multiplica por el denominador de la segunda, al tiempo que el denominador de la segunda fracción se multiplica por el numerador de la otra expresión involucrada. Esta operación podrá representarse matemáticamente de la siguiente manera:

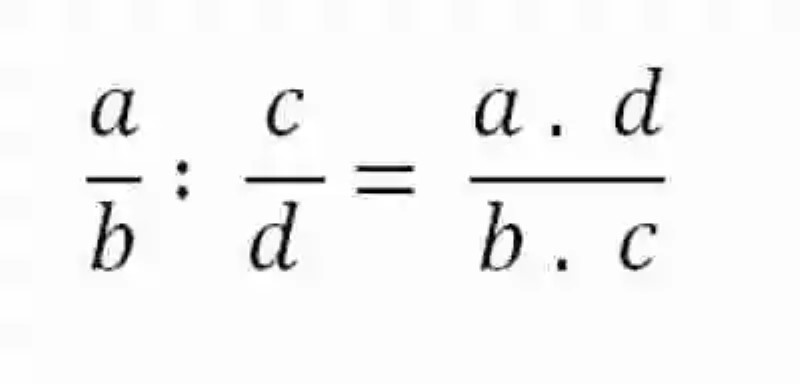
Propiedades de la División de fracciones

Una vez se han revisado estas definiciones, tal vez ciertamente sea mucho más sencillo aproximarse a cada una de las propiedades presentes o ausentes en la División de fracciones, las cuales también deberán ser estudiadas según existan o no en esta operación, tal como se muestra a continuación:

Propiedades existentes en la División de fracciones

En el caso de las Propiedades matemáticas que sí pueden encontrarse en la División de fracciones, las Matemáticas señalan que se pueden distinguir dos de ellas:

• Propiedad Interna: esta propiedad señalará que siempre que se realice una División en la que participen dos o más fracciones, el resultado será siempre y si excepción otra fracción, de ahí que reciba el nombre de Propiedad Interna, puesto que el cociente obtenido pertenecerá también a los números fraccionarios.
• Propiedad distributiva: en segundo lugar, las Matemática señalarán que en la División de fracciones podrá hablarse también de la Propiedad distributiva, la cual se da siempre en relación a la suma, toda vez que esta operación ocupe el lugar del diviso, pues de lo contrario la Propiedad será imposible. De esta forma, siempre que una suma de fracciones se divida entre otra fracción, esta ley matemática dicta que se podrá resolver la operación, dividiendo cada sumando entre la fracción que los divide a ambos, y luego sumar los respectivos resultados. Esta Propiedad puede expresarse de la siguiente manera:

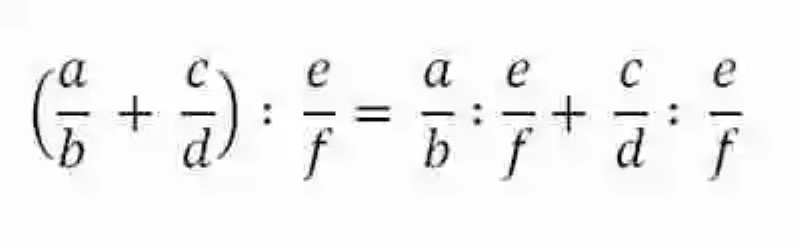
Propiedades no existentes en la División de fracciones

Por otro lado, será también pertinente explicar cuáles son las propiedades matemáticas que no se encuentran o no son posibles en la División de fracciones, y que según coinciden las diferentes fuentes, se trataría entonces de las siguientes:

• Propiedad conmutativa: de acuerdo a lo que señalan los diversos autores, en la División de fracciones no podrá hablarse de Propiedad conmutativa, puesto que toda vez se haya planteado una división, cualquier cambio o inversión entre sus respectivos factores, originará un cambio en el resultado. Esta Ley podrá ser expresada tal como se ve a continuación:

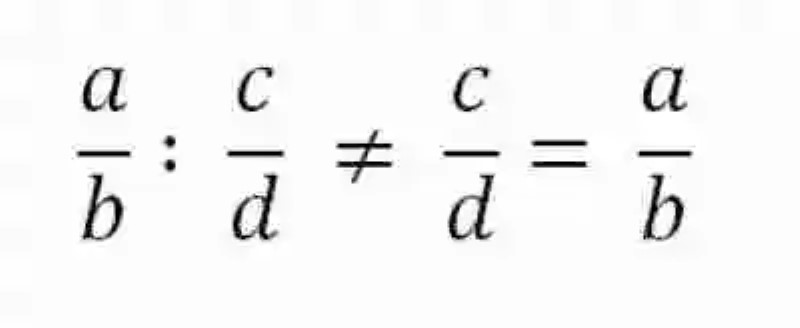
• Propiedad asociativa: así mismo, las Matemáticas indican que una vez se haya planteado una división entre tres o más fracciones, estas no contarán con la posibilidad de establecer diferentes relaciones entre sí, sin que esto no se traduzca en un cambio a los cocientes obtenidos, por lo que entonces se afirma que en la División de fracciones no es posible que suceda la Propiedad asociativa. Esta ley matemática contará con la siguiente expresión:

Imagen: pixabay.com

s

s

s

s

s

s

x

+d+d+d+s

s

s

ss

s

s

s

s

}}}}}}}}}}}}}}}}