
Tabla de contenido
Quizás lo mejor, previo a avanzar en una explicación sobre las diferentes propiedades matemáticas, presentes en la División de fracciones, sea revisar de forma breve algunos conceptos, indispensables para entender cada una de estas leyes matemáticas en su contexto preciso.
Definiciones fundamentales
En este sentido, puede entonces que también sea prudente delimitar esta revisión teórica a dos nociones específicas: las Fracciones y la División de fracciones, por ser estas respectivamente la expresión y la operación matemática en donde tienen lugar tanto la Propiedad interna como la Distributiva. A continuación, cada uno de estos conceptos:
Fracciones
De esta manera, se comenzará por señalar que las fracciones han sido explicadas como un tipo de expresión matemática, usada para representar cantidades no exactas o no enteras, de ahí que se entiendan también como una de las dos formas matemáticas usadas para dar cuenta de números fraccionarios.
Por otro lado, la disciplina matemática también ha señalado que las fracciones se encontrarán conformadas sin excepción por dos elementos, cada uno de los cuales podrán ser definidos de la siguiente manera:
- Numerador: en primer lugar, el Numerador será visto como el elemento que da cuenta de las partes que se han tomado del todo. Siempre ocupará la parte superior de la fracción.
- Denominador: por otro lado, la fracción contará con un segundo elemento, el cual ocupará siempre la parte inferior de la expresión, recibiendo el nombre de Denominador. Su tarea será señalar en cuántas partes se encuentra dividido el todo, del cual se ha tomado una o varias partes.
División de fracciones
Así mismo, será importante lanzar luces sobre el concepto de División de fracciones, operación que es descrita como el procedimiento matemático empleado con el fin de determinar cuántas veces se encuentra incluida una fracción en otra, es decir, cuál es el cociente resultante de dividir una fracción que hace las veces de dividendo entre una segunda expresión, la cual funge como divisor.
Respecto a la forma correcta de resolver este tipo de operaciones, las Matemáticas también han señalado que lo mejor será implementar el método de la multiplicación cruzada, la cual plantea que deberá multiplicarse el numerador de la primera fracción por el denominador de la segunda expresión, así como el denominador de la fracción que sirve de dividendo por el numerador del divisor, lo cual podrá expresarse matemáticamente de la siguiente manera:
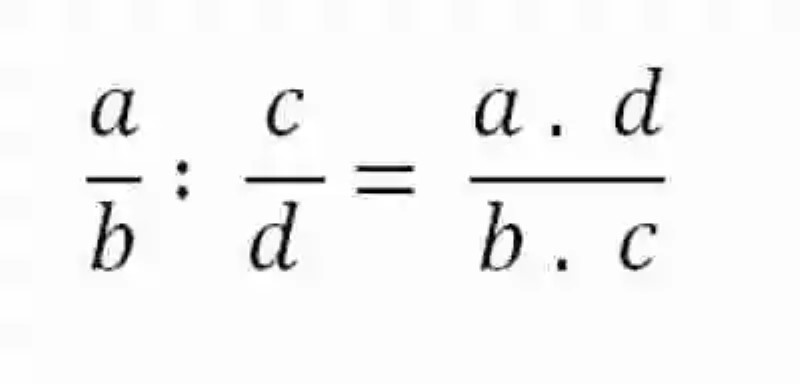
Propiedades matemáticas presentes en la división de fracciones
Teniendo presente cada una de estas definiciones, quizás entonces resulte mucho más sencillo entender cada una de las leyes matemáticas, que pueden encontrarse en la operación de división de fracciones, y que según señalan las distintas fuentes serán básicamente dos: la Propiedad interna y la Propiedad distributiva, leyes matemáticas que han sido explicadas a su vez de la siguiente manera:
Propiedad interna
En consecuencia, en cuanto a la Propiedad interna que existe en la División de fracciones, básicamente promulgará que siempre y sin excepción que se realice una operación de este tipo, el resultado será igualmente una fracción, de ahí que también reciba el nombre de Propiedad interna, puesto que los cocientes obtenidos siempre pertenecerán a los números fraccionarios, en específico a las fracciones.
La única excepción que plantea esta propiedad matemática es cuando el dividendo es cero, puesto que resulta un imposible matemático tratar de averiguar cuántas veces cabe una fracción en la ausencia plena de cantidad. De esta manera, toda división que cuente con el dividendo igual a cero será imposible, por lo que se considera que no da como resultado una fracción, por lo que se dice entonces que no se cumple la Propiedad Interna.
Propiedad distributiva
En segundo lugar, en la División de fracciones podrá encontrarse también la Propiedad distributiva, la cual se explica como la Ley matemática que se cumple toda vez que una suma ejerce como dividendo en una división con otra fracción, entendiéndose entonces que esta operación podrá ser resuelta, gracias a la Propiedad Distributiva, a través de la división de cada uno de los sumandos con la tercera fracción, para luego sumar los resultados. Esta propiedad podrá expresarse por su lado de la siguiente manera:
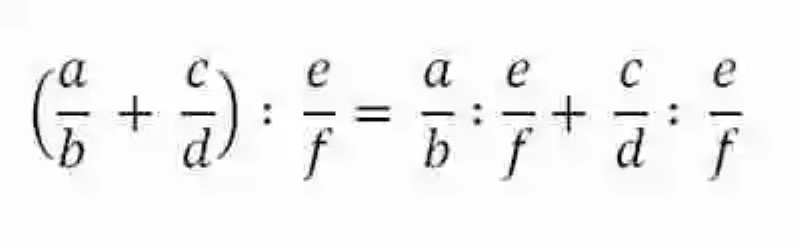
Imagen: pixabay.com
El pensante.com (enero 31, 2018). Propiedades presentes en la división de fracciones. Recuperado de https://elpensante.com/propiedades-presentes-en-la-division-de-fracciones/