Proporción continua

Definiciones fundamentales

En este sentido, puede que sea necesario entonces delimitar esta revisión a dos nociones específicas: Razones y proporciones, por encontrarse directamente relacionados con la relación que se estudiará posteriormente. A continuación, cada uno de ellos:

Razones

De esta manera, se comenzará por decir que las Razones han sido explicadas por las diferentes fuentes como una expresión matemática que da cuenta del cociente de dos números, lo cual podrá tener la siguiente forma:

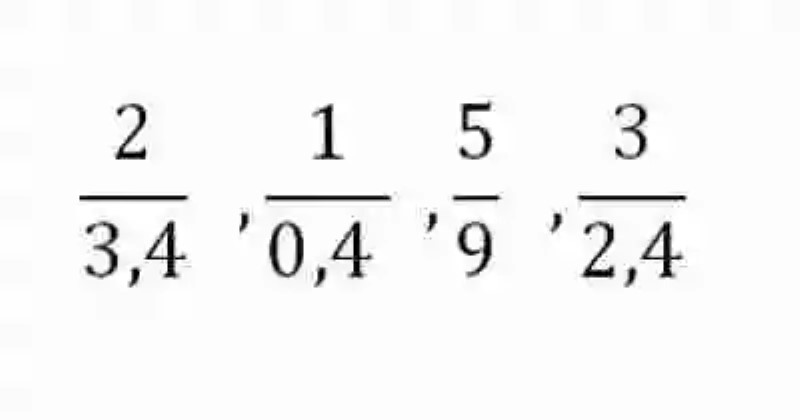
Sin embargo, en este punto, será necesario señalar la importancia de no confundir los conceptos de razones con los de fracciones. En este orden de ideas, se señalará entonces que mientras las fracciones –constituidas por los numeradores y denominadores, que además siempre resultarán ser números enteros- dan cuenta de la cantidad que se ha tomado de una unidad, dividida a su vez en partes iguales, las razones –constituidas por el ascendente y el consecuente, los cuales pueden resultar números no pares- darán cuenta del cociente de un número, es decir, de cuántas veces se encuentra contenido el Divisor dentro del Dividendo.

Proporciones

En segunda instancia, será necesario también pasar revista sobre la definición de Proporción, la cual ha sido explicada como la relación de igualdad que existe entre dos razones, cuando estas arrojan el mismo cociente al ser desarrolladas. No obstante, puede que sea necesario también contar con un ejemplo:

Si se tuviera la siguiente razón:

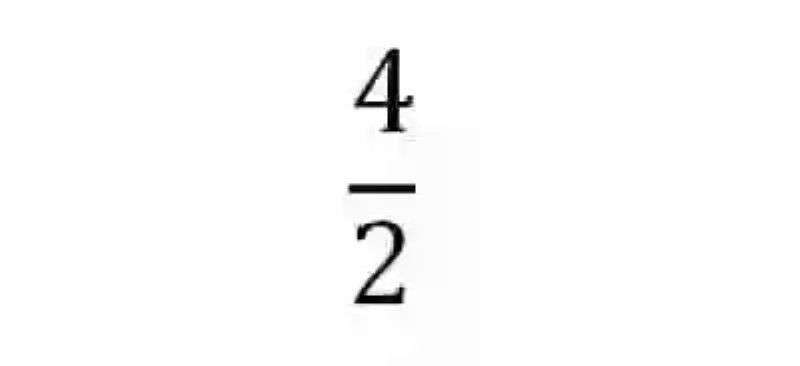
Así como la siguiente aplicación lineal: y = 3 . x Se tendrían entonces los siguientes originales e imágenes:

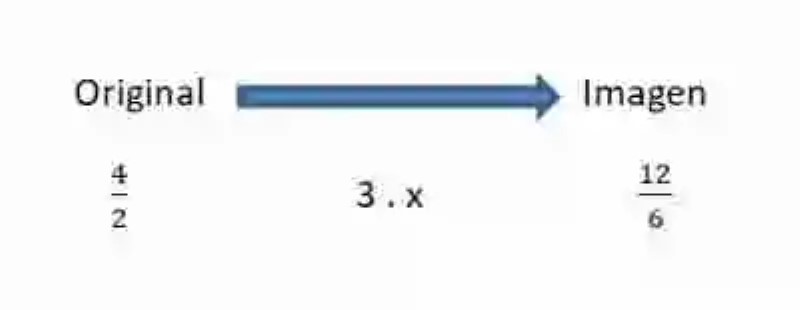
Al resolver ambas razones se obtendrán el mismo cociente, por lo que se les considerará proporcionales, por ser razones iguales. Empero, esta no es la única forma de comprobar la proporción de dos razones, sino que al multiplicar entre sí sus medios –constituidos por el consecuente de la primera razón y el ascendente de la segunda- así como sus extremos –conformados por el ascendente de la primera razón y el consecuente de la segunda- ambos productos deben coincidir, relación esta que ha sido representada de la siguiente forma:

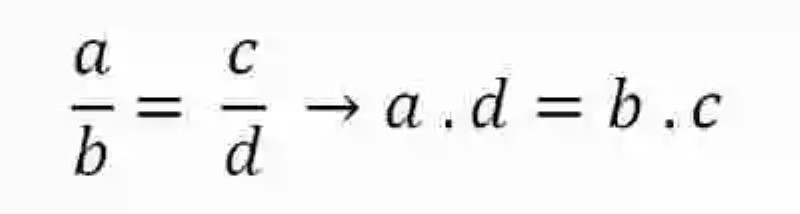
Si aplicáramos esta relación a las siguientes razones iguales, se obtendría lo siguiente:

Lo cual hace posible que se pueda conocer cualquiera de los miembros de una razón, que resulte proporcional a otra.

Proporción continua

Una vez se han explicado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre la Proporción continua, la cual ha sido explicada como la proporción que se da entre dos razones, que cuentan con medios que resultan iguales, es decir, dos razones en donde tanto el consecuente de la primera expresión como el antecedente de la segunda cuentan con igual valor. Un ejemplo de Proporción continua sería el siguiente:

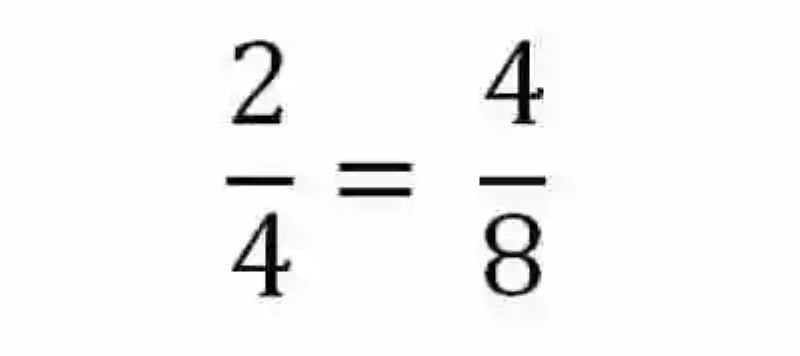
Esta relación de proporción continua será usada para determinar también la media geométrica, la cual explicaría que tal como x² = a . b entonces x = √ a. b

Por lo tanto, si se desconocieran los medios de dos razones iguales, a través de esta fórmula, se podrían conocer, solo sabiendo los extremos. Si se tomarán entonces estas proporciones, en el que no se conocieran los medios, se tendría lo siguiente:

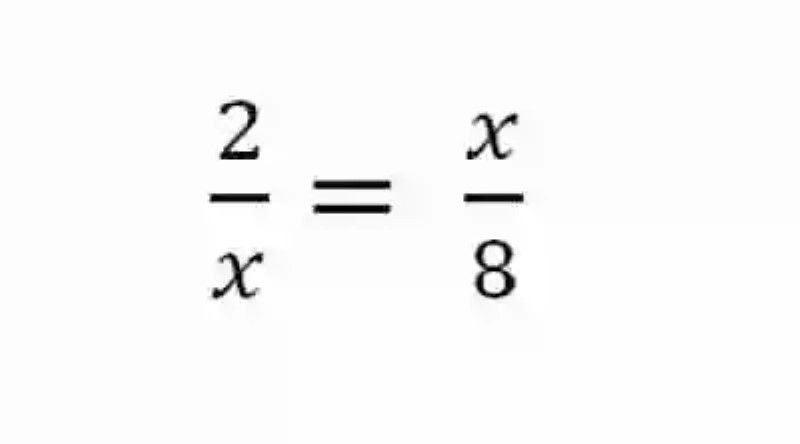
Al momento de determinar entonces los medios de esta proporción, será necesario aplicar la siguiente fórmula:

Se obtiene entonces que x es igual a 4, por lo que se puede completar entonces la proporción, la cual contando con iguales medios será considerada una Proporción continua: