Proyección de un punto sobre una recta

Definiciones fundamentales

En este sentido, puede que también sea necesario enfocar esta revisión teórica a dos nociones fundamentales: Punto, Recta y Rectas perpendiculares, por ser las entidades geométricas, directamente relacionadas con esta operación geométrica. A continuación, cada una de ellas:

Punto

De esta manera, se comenzará por decir que la Geometría considera al punto como la entidad geométrica más elemental, así como una de las esenciales, posición esta que comparte con la Recta. Así mismo, la Geometría ha definido al Punto como una entidad que no cuenta con ningún atributo geométrico, es decir, que no tiene dimensiones, ni altura, ni ninguna otra. De hecho, no será considerada en sí misma una figura geométrica, sino la ubicación de un objeto dentro de un plano o sistemas de coordenadas.

Recta

Por otro lado, la Geometría también se ha dado a la tarea de definir la Recta, la cual es explicada por las distintas fuentes como una figura geométrica unidimensional, es decir, que cuenta solo con una dimensión. Por igual, esta disciplina ha indicado que la Recta puede ser explicada como una sucesión infinita de puntos, los cuales deben contar con la misma dirección. Empero, este requisito no convierte para nada a la Recta en una figura con una sola orientación posible, ya que de hecho podrá contar con dos distintos sentidos, los cuales dependerán directamente de la lectura que se realice sobre esta figura. Así mismo, la Recta se distinguirá por contar con los siguientes rasgos:

• en primer lugar, la Recta ha de ser vista también como la distancia más corta entre dos puntos.
• de igual manera, la Geometría señala que la Recta puede ser descrita como la única figura geométrica que puede pasar por medio de ellas.
• también, esta disciplina afirma que entre dos puntos solo podrá pasar una recta por oportunidad.
• finalmente, la Recta deberá ser representada siempre por una letra minúscula.

Rectas perpendiculares

Por último, también será necesario señalar cuál es la definición de Rectas perpendiculares, las cuales deberán ser interpretadas como aquellas líneas rectas, es decir figuras unidimensionales constituidas por sucesiones infinitas de puntos, que se cortan entre sí de forma perpendicular, en algún lugar de su extensión. Esto se explica gráficamente como una recta horizontal que se corta con una recta vertical, y que en su disposición e intersección crean también cuatro ángulos rectos, entendiéndose esto como cuatro ángulos de 90º.

Proyección de un punto sobre una recta

Una vez se han revisado cada una de estas definiciones, será mucho más sencillo entender los elementos geométricos con los cuales deben realizarse la proyección de un punto sobre la recta. En este orden de ideas, se comenzará por decir entonces que toda vez que se tenga una recta determinada y un punto, que se ubique en el mismo plano que la recta, pero a una distancia determinada, podrá hacerse una proyección ortogonal de este punto sobre la recta, lo cual se podrá hacer trazando desde el punto una línea perpendicular con la cual se une el punto y la recta, y que constituirá dicha proyección.

Ejemplo de cómo realizar la proyección ortogonal

Sin embargo, puede que la mejor manera de abordar una explicación sobre este procedimiento geométrico sea exponer un ejemplo concreto, en donde se pueda ver cómo debe ser realizado este procedimiento, tal como puede verse a continuación:

1.- Dada una recta y un punto determinados, y ubicados en el mismo espacio, se deberá comprobar que el punto se encuentra en una posición desde la cual realmente se pueda trazar una línea perpendicular entre estas dos entidades:

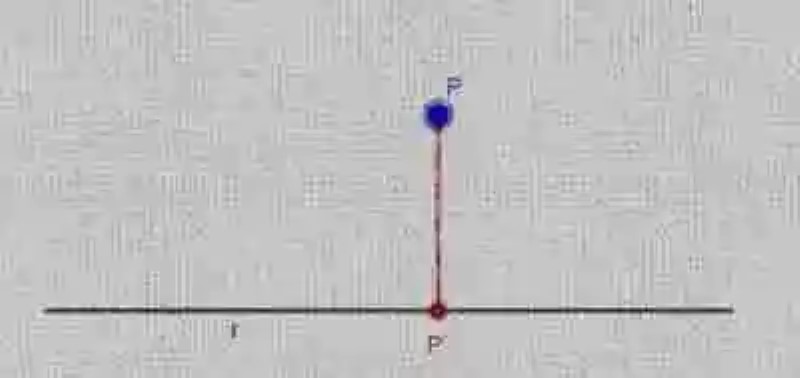
2.- Al hacerlo, simplemente se trazará la línea perpendicular, que una el punto con la recta, pues esta perpendicular será la proyección ortogonal. Hecho esto, se considera terminado el procedimiento.

Imágenes: 1.- pixabay.com / 2.- wikipedia.org