Racionalización de denominadores

Definiciones fundamentales

En este sentido, puede que también sea pertinente delimitar esta revisión a dos nociones específicas: Fracciones y Radicación, por ser estas las expresiones y operaciones, directamente relacionadas con el procedimiento por medio del cual se logra la Racionalización de denominadores. A continuación, cada uno de estos conceptos:

Fracciones

De esta manera, se comenzará por decir que las Matemáticas han explicado las fracciones como uno de los dos posibles tipos de expresión con los que cuentan los números fraccionarios o racionales, es decir, que las fracciones serán expresiones matemáticas que sirvan para representar cantidades no exactas o no enteras. Así mismo, las fracciones son señaladas por la mayoría de las fuentes como una expresión compuesta por dos elementos, cada uno de los cuales ha sido explicado de la siguiente forma:

• Numerador: en primer lugar, el Numerador será asumido como el elemento numérico que ocupa la parte superior de la fracción. Su misión básicamente es la de indicar cuántas partes del todo se han tomado, o son representadas por la fracción.
• Denominador: por otro lado, el Denominador puede ser entendido como el elemento que se encuentra ubicado en la parte inferior de esta expresión. Cuenta con la tarea de indicar en cuántas partes se encuentra dividido el todo, del cual el numerador señala solo algunas, y en algunas ocasiones todas.

Radicación

En otro orden de ideas, será necesario también detenerse en el concepto de Radicación, operación matemática cuyo principal propósito, según señalan los diferentes autores será determinar cuál es el número, que una vez elevado al índice que propone originalmente la operación, da como resultado el radicando que esta también plantea desde el principio. En consecuencia, se podría asumir también la Radicación como una expresión inversa de la Potenciación, puesto que si la operación se plantear en estos términos, se estaría buscando entonces la base.

Racionalización de denominadores

Una vez se han revisado cada uno de estos conceptos, podrá profundizarse de forma más sencilla en la definición de Racionalización de denominadores, operación matemática, cuya principal motivación es sacar de la raíz el número que sirve de denominador en una fracción, a fin de poder reducir la expresión matemática a una forma más reducida, lo cual no podría realizarse teniendo como denominador un radical.

Sin embargo, la operación que implica la racionalización de denominadores puede encontrarse con dos realidades, según si el denominador no cuenta con sumas o restas en su configuración, o si por el contrario sí las presenta, casos que implican por su parte maneras distintas de asumir el proceso de racionalización de denominadores. A continuación, cada una de las posibles opciones:

Si en el denominador no se presentan sumas o restas

En caso de que el denominador de una fracción sea un radical, el cual no se sume o reste con ningún otro elemento, y se desee aplicar un procedimiento de racionalización, se deberá tomar cada uno de los elementos de la fracción y multiplicarlos por el radical que constituye el denominador, a fin de obtener un cuadrado de este, que le permita salir de la raíz. Este procedimiento podría expresarse matemáticamente de la siguiente manera:

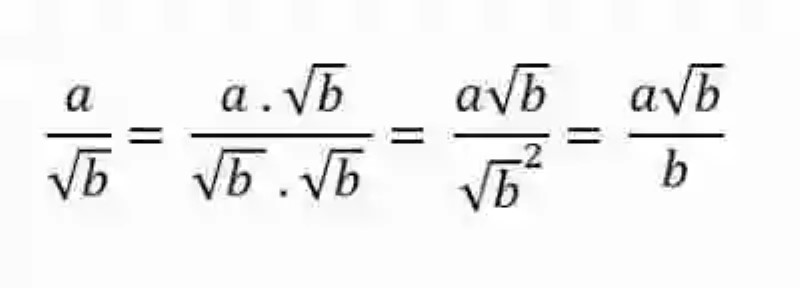
Sin embargo, puede que sea necesario ofrecer un ejemplo concreto de cómo proceder ante una Racionalización de denominadores, que implique un elemento en el cual no se presenten ni sumas ni restas, tal como el que se muestra a continuación:

Si el denominador sí presenta sumas o restas

Por el contrario, puede ocurrir también que el Denominador que se desea racionalizar cuenta en sí con operaciones de suma o resta, por lo que en este caso será necesario multiplicar cada uno de los elementos de la fracción, es decir, el numerador y el denominador por la expresión conjugada del denominador, la cual corresponderá con las siguientes lógicas:

Si la expresión es (a – b) la expresión conjugada será (a + b)
Si la expresión es (a + b) la expresión conjugada será (a – b)

En consecuencia, el procedimiento de racionalización de denominadores, en caso de que este cuente con un elemento en donde existan sumar o restas, podrá expresarse matemáticamente de la siguiente manera:

Si por el contrario, en el denominador se planteara una resta, se procedería de la siguiente manera:

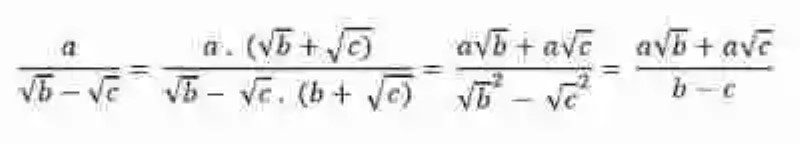
Se asume por demás que siempre la lógica de multiplicar una suma o resta por su expresión conjugada, implicará lo siguiente:

a + b . (a – b)=  a² – b²

No obstante, puede que también sea necesario exponer un ejemplo concreto, que permita ver de forma práctica cómo debe cumplirse cada uno de los pasos que implica racionalizar un denominador en donde hay presencia de sumas o restas, tal como puede verse a continuación:

Racionalizar el denominador en la siguiente fracción:

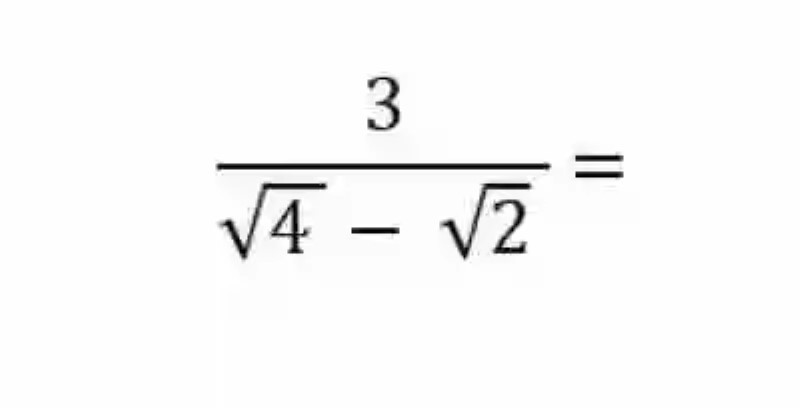
Para dar solución a esta operación se deberá multiplicar entonces cada elemento por la expresión conjugada del denominador:

Se tomará este como el resultado final de la operación de racionalización de denominadores, en vista de que se ha cumplido con la misión de extraer los elementos del denominador de los radicales que los arropaban.

Imagen: pixabay.com