Raíz cuadrada exacta

La radicación

En primer lugar, se podrá decir entonces que la mayoría de fuentes teóricas coinciden en señalar a la Radicación como una operación matemáticas, en donde dos números tratan de determinar un tercero, que tenga la capacidad de multiplicarse por sí mismo, tantas veces como señale uno de los números involucrados en la operación, dando como resultado el otro número implicado, de ahí que la Radicación haya sido explicada también por algunos autores como una operación de Potenciación inversa, o incluso como otra forma de expresar la Potenciación.

Elementos de la Radicación

Así mismo, puede resultar de gran importancia, en el entendimiento de la Radicación, al igual que de la Raíz cuadrada, pasar revista sobre la definición de cada uno de los elementos que constituyen una operación de Radicación, y que han sido explicados de la siguiente manera: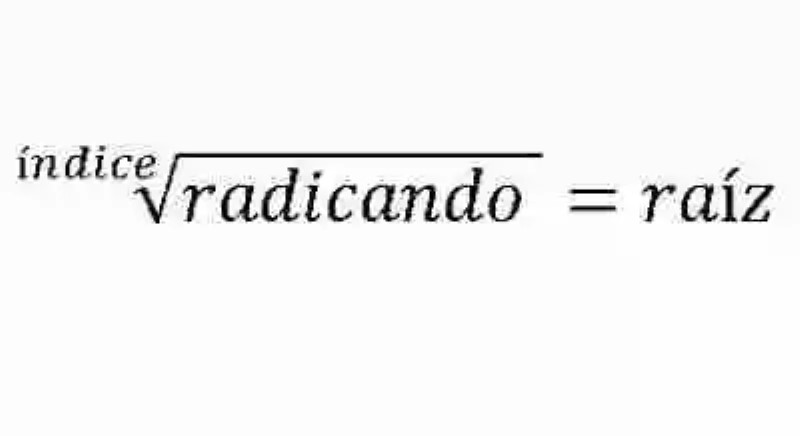

• Índice: en primera instancia se encontrará el índice, el cual cumple con la función de señalarle a la raíz cuál es el número de veces que deberá multiplicarse a sí misma, a fin de originar como producto un número equivalente al radicando. El índice se anotará en la esquina superior izquierda del signo radical.
• Radicando:  por su parte, el Radicando será el otro número en base al cual se llevará a cabo la operación de Radicación. Su función será señalarle a la raíz cuál debe ser el resultado de su multiplicación por sí misma, tantas veces como señale el índice.
• Raíz: de esta manera, la Raíz será asumida como el resultado final de la operación, así como el número que cumple con la tarea de señalar cuál sería la base de una Potencia constituida por el radicando, teniendo al índice como exponente.
• Signo: finalmente, el signo será considerado también parte de la operación de Radicación. En este caso, será ejercido por el símbolo radical, siendo su función ubicarse entre el índice y el radicando, a fin de señalar que entre ellos ocurre una operación de radicación.

Raíz cuadrada

Entre otras de las definiciones fundamentales que deben abordarse en pro del entendimiento de la Raíz cuadrada exacta se encuentra el concepto mismo de Raíz cuadrada, la cual ha sido explicada en rasgos generales, por las distintas fuentes matemáticas, como toda operación de Radicación, caracterizada por contar con un índice igual a 2.

Así también esta operación se caracteriza por no presentar un índice explícito, es decir, que por tradición, al momento de expresar una Raíz cuadrada, no se colocará ningún tipo de índice en el signo del radical, sobrentendiéndose que este es igual a 2.

Por otro lado, se podría decir entonces que una Raíz cuadrada será una operación en donde dos números –siendo uno de ellos el 2, que cumple función de índice- buscarán determinar cuál número, al multiplicarse por sí mismo dos veces, es decir, elevarse al cuadrado, da como resultado el Radicando.

Raíz cuadrada exacta

Teniendo presente estas definiciones, quizás entonces sea mucho más sencillo comprender el concepto de Raíz cuadrada exacta, estipulado por las Matemáticas, el cual puede explicarse como toda Raíz cuadrada, que origine una raíz que al ser elevada al cuadrado dé como resultado exactamente el radicando, es decir, toda raíz cuadrada que tenga como radicando un cuadrado perfecto.

Ejemplos de Raíz cuadrada exacta

Sin embargo, quizás la forma más eficiente de completar una explicación sobre la Raíz cuadrada exacta sea a través de la exposición de algunos ejemplos, en donde se pueda ver cómo al tratarse de este tipo de operaciones, se consigue en cada caso raíces que al ser elevadas al cuadrado, producen de forma exacta el número que cumple el papel de Radicando. A continuación, algunos ejemplos:

√16 = 4 → 4² = 16

√25 = 5 → 5² = 25

√36= 6 → 6² = 36

√100 = 10 → 10² = 100

√4 = 2 → 2² = 4

√9= 3 → 3² = 9

Imagen: pixabay.com