
Antes de avanzar sobre una explicación respecto a la propiedad matemática, conocida como Raíz de un cociente, quizás sea conveniente revisar de forma breve la definición misma de Radicación, a fin de comprender esta Ley, dentro de su contexto matemático.
La radicación
De esta manera, resulta pertinente señalar que las Matemáticas han explicado la Radicación como una operación que sucede entre dos números, los cuales tratan de hallar un tercero, caracterizado por la cualidad de multiplicarse a sí mismo, la cantidad de veces que índice uno de los números involucrado en la operación, y dar como resultado al otro de los números participantes, hecho que implica también que la mayoría de los autores reconozcan a la Radicación como una operación inversa a la Potenciación.
Elementos de la radicación
Así mismo, la disciplina matemática se ha dado a la tarea de promulgar una definición hacia cada uno de los elementos, sobre los cuales están constituida esta operación, y que han sido descritos de la siguiente manera:
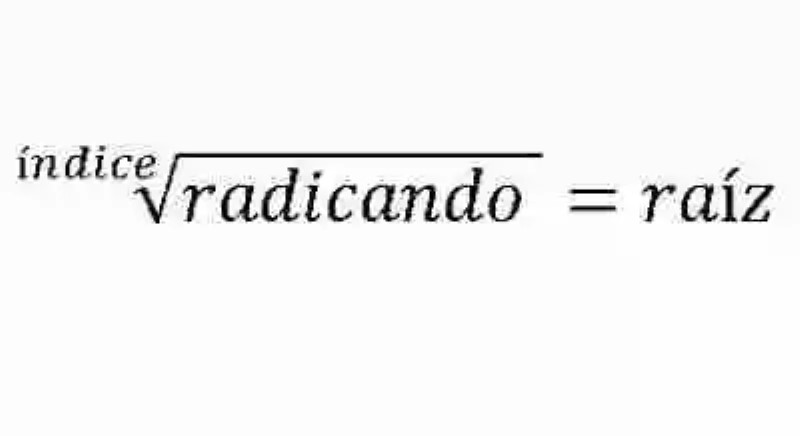
- Índice: en primer lugar, las Matemáticas señalan al índice como el número que se ubica, por fuera del signo de la operación, en su esquina superior izquierda. Se le atribuye la misión de señalarle a la raíz cuántas veces debe multiplicarse a sí misma, a fin de dar como resultado el radicando. Si la operación se expresara en forma de potenciación, el índice sería equivalente al exponente.
- Raíz: por su parte, la raíz ha sido explicada como el resultado final de la operación, así también como el número que tiene la cualidad de multiplicarse por sí mismo, tantas veces como señale el índice, dando como resultado el radicando. Si se piensa en términos de potenciación, la Raíz podría ser interpretada como la base de la operación.
- Radicando: de esta manera, el radicando sería entonces el producto obtenido en base a la multiplicación de la Raíz, tantas veces como ha señalado el índice. Es el segundo número involucrado en la operación. Si esta fuese expresada como una potenciación, al Radicando le correspondería entonces cumplir las veces de potencia.
- Signo: finalmente, el signo estará constituido por el símbolo √ conocido con el nombre de radical. Su misión es ubicarse entre el índice y el radicando, a fin de señalar que entre ellos ocurre una operación de radicación.
¿Cómo resolver una operación de radicación?
Sin embargo, la mejor forma de completar una explicación sobre la radicación será exponiendo un caso concreto, que permita ver de cerca cómo se resuelve esta operación, al menos en sus presentaciones más básicas, puesto que generalmente a la hora de resolver la raíz de un número, lo mejor será apoyarse en una calculadora, al menos que se cuenten con avanzados conocimientos matemáticos. A continuación, un ejemplo de radicación:
Suponiendo que se cuente con el número 8, y se desee calcular su raíz cúbica, será necesario seguir los siguientes pasos:
1.- Lo primero que se hará será plantear la operación en términos matemáticos, tomando en cuenta entonces que el 8 cumplirá el papel de radicando, mientras que al ser una raíz cúbica, le corresponde al número 3 hacer las veces de índice: ∛8
2.- Hecho esto, se deberá entonces encontrar un número, para la raíz, que cumpla con la propiedad de que al multiplicarse a sí mismo, en tres oportunidades, como señala el índice, dé como resultado 8, es decir, el número que sirve de radicando. De esta manera, se recurre entonces a la operación de la potenciación:
13 = 1
23 = 8
3.- Debido a que es una operación de números pequeños, rápidamente se encuentra que el número que cumple con los requerimientos de originar 8, en base a multiplicarse tres veces por sí mismo es el 2, por lo que es interpretado entonces como la raíz, es decir, el resultado final de la operación de radicación: ∛8= 2
Propiedad Raíz de un cociente
Teniendo presente estas definiciones, quizás sea mucho más sencillo abordar una explicación sobre la propiedad matemática, inherente a la Radicación, la cual es conocida por el nombre de Raíz de un cociente, y que dicta que toda vez que siempre que se esté frente a la raíz de una fracción, esta arrojará igual resultado que el cociente obtenido en base a dividir la raíz del denominador entre la raíz del numerador.
Igualmente, la mayoría de las fuentes coinciden en señalar que la propiedad matemática de la Raíz de un cociente puede ser también expresada matemáticamente de la siguiente manera:
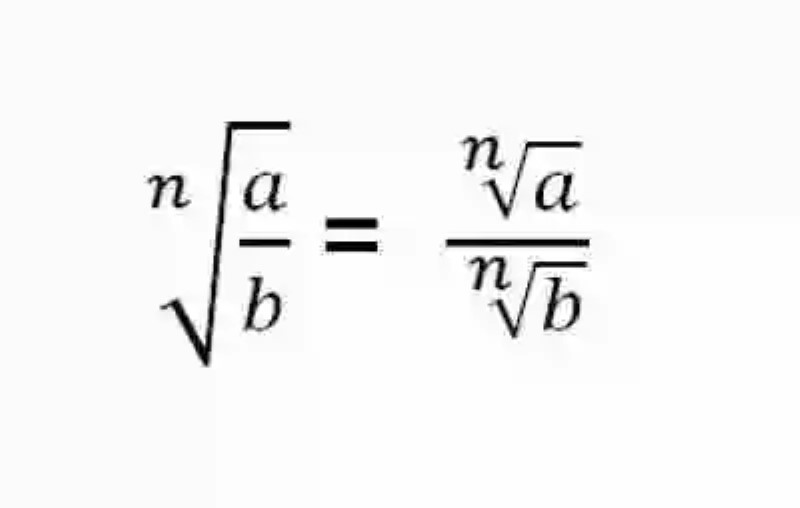
Ejemplo sobre la propiedad Raíz de un cociente
Sin embargo, quizás la mejor manera de completar una explicación sobre esta propiedad matemática que puede encontrarse en la Radicación, será a través de un ejemplo concreto, en donde pueda verse de cerca, si efectivamente se encuentran iguales resultados, si se calcula la raíz de la fracción, o por el contrario se obtiene un cociente en base a la división de las raíces de cada número de la fracción, tal como se ve en el caso que se muestra a continuación:
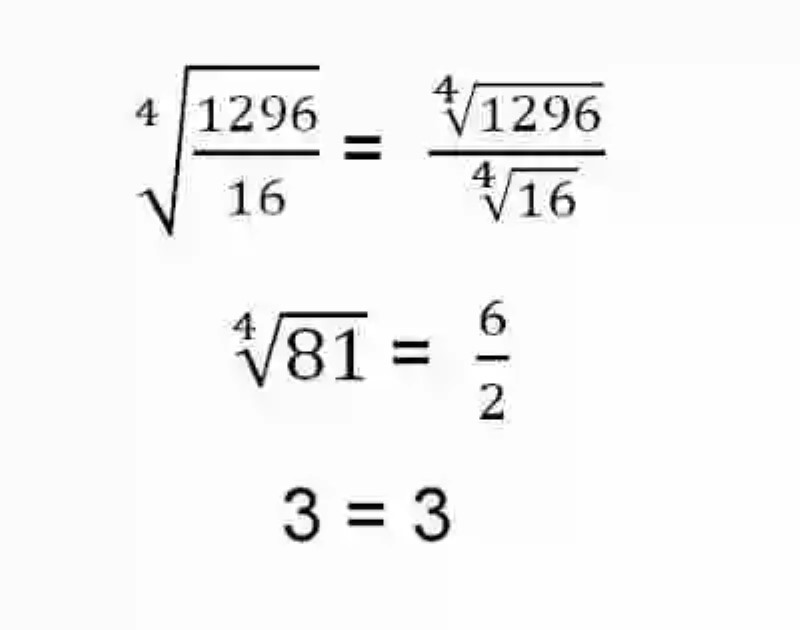
Imagen: pixabay.com
El pensante.com (octubre 26, 2017). Raíz de un cociente. Recuperado de https://elpensante.com/raiz-de-un-cociente/