
Antes de avanzar en las respectivas definiciones que pueden haber sobre las Razones y las Proporciones, quizás lo más recomendable hacer una breve revisión respecto a algunas definiciones, que de seguro permitirán entender este tipo de expresiones dentro de su justo contexto matemático.
Definiciones fundamentales
En este sentido, puede que también sea recomendable delimitar esta explicación a dos conceptos específicos: Fracciones y Cociente, por encontrarse directamente relacionadas con la posibilidad de poder entender las fracciones y las proporciones. A continuación, cada uno de estos conceptos:
Fracciones
En primer lugar, se encontrarán las fracciones, las cuales serán explicadas como una expresión matemática que refiere a la parte de una unidad, que a su vez ha sido dividida en partes iguales. De acuerdo a lo que señalan las distintas fuentes, una fracción se encontrará conformada a su vez por dos partes:
- Numerador: parte de la fracción que señala cuántas partes de la unidad se han tomado, o representa la fracción.
- Denominador: parte de la fracción que indica en cuántas partes iguales ha sido dividida la unidad.
Más que en el ámbito matemático, las fracciones resultan bastante usadas y útiles en la cotidianidad, pues sirven para expresar por ejemplo cuántas porciones de pizza o pastel se han tomado, o cuántos módulos de una materia han sido aprobados.
Cociente
Por otro lado, también será necesario revisar el concepto de Cociente, el cual ha sido explicado como un elemento más de la división, cuya función es indicar cuántas veces el número que sirve de Divisor se encuentra contenido en el Dividendo. Por ejemplo, si se realizara una división en donde el número 10 fuese el Dividendo y el número 5 hiciera las veces de Divisor, se tendría entonces como resultado el número 2, el cual sería identificado como cociente, puesto que estaría revelando que el número 5 se encuentra contenido 2 veces en el número 10.
Razones y proporciones
Una vez se han revisado estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre las Razones y las proporciones, expresiones matemáticas que serán necesarios para poder entender el concepto de Magnitudes proporcionales, así como el de Regla de tres. A continuación, cada una de estas definiciones:
Las razones
En primer lugar, se encontrarán las Razones, las cuales básicamente han sido definidas por las Matemáticas como el cociente que puede existir entre dos números. Las razones pueden expresarse de la siguiente forma:
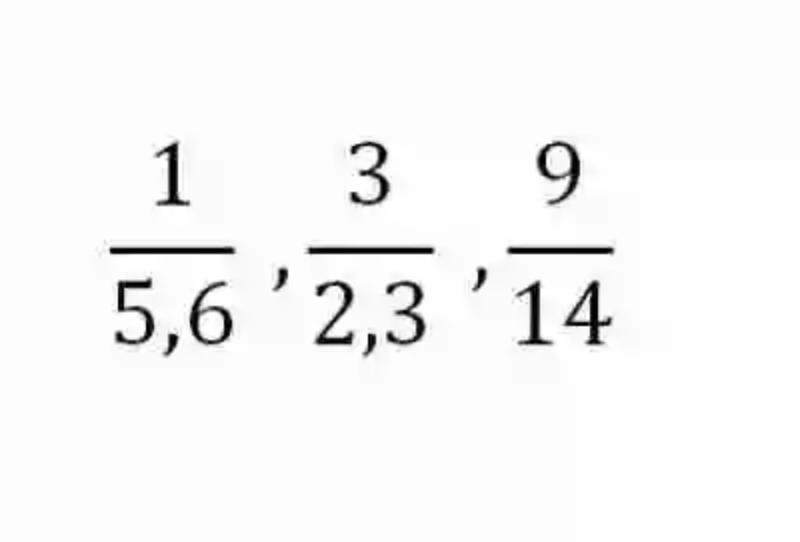
Sin embargo, las Matemáticas advierten la importancia de no confundir las razones con fracciones, puesto que si coinciden en cuanto a su forma, la principal diferencia será que mientras las fracciones estarán conformadas siempre por números enteros, que ocupen respectivamente la posición de numerador y denominador, cada una de las partes que conforman a las razones pueden ser números decimales.
Por otro lado, la disciplina matemática señala también que las partes que conforman una razón son llamados de la siguiente forma:
- el antecedente, el cual ocupará el lugar del numerador de la razón,
- mientras que el consecuente fungirá como el denominador.
Proporciones
En el caso de las Proporciones, las Matemáticas han señalado que esta puede ser definida como la igualdad que existen entre dos razones, y que puede ser determinada si esta igualdad ocurre entre las imágenes, es decir, si las razones originales son iguales a las razones formadas por las imágenes, y mientras esta sea constante.
Por ejemplo, si se tuviera una aplicación lineal y = 3. x, y se decidiera aplicarla en la razón en donde antecedente y consecuente asumen x respectivamente se tendría lo siguiente:
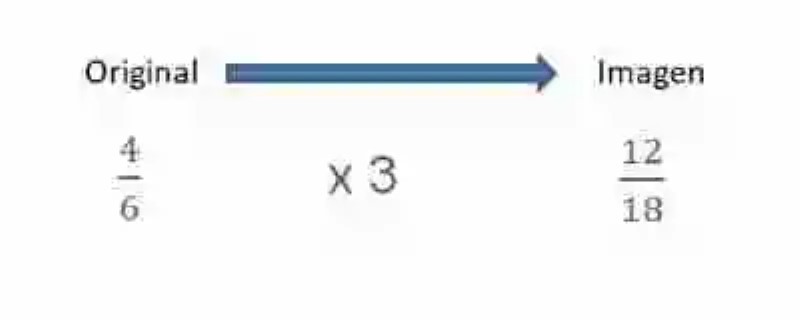
Si se resolviera cada una de estas razones, se obtendría el mismo cociente, por lo que al ser iguales se puede decir entonces que entre ellas existe proporción.
Imagen: pixabay.com
El pensante.com (octubre 17, 2018). Razones y proporciones. Recuperado de https://elpensante.com/razones-y-proporciones/