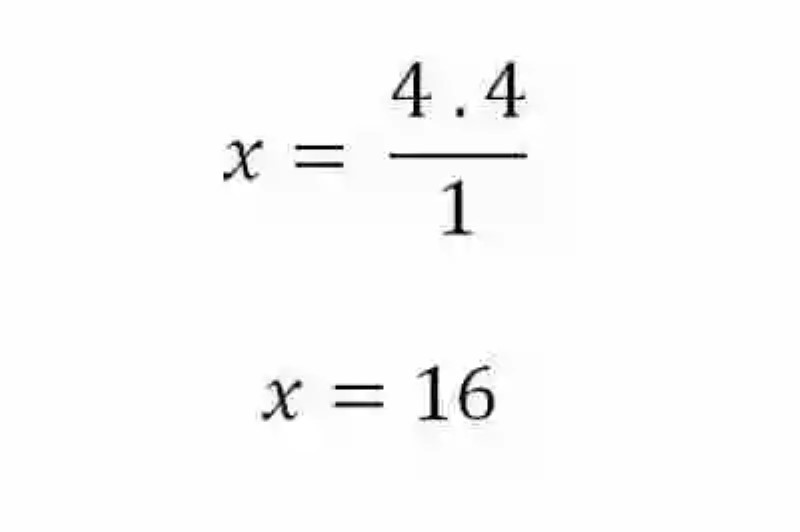Regla de tres directa

Definiciones fundamentales

En este sentido, puede que también resulte importante delimitar esta revisión teórica a tres nociones específicas: Razones, Proporciones y Magnitudes directamente proporcionales, pues estos conceptos se encuentran relacionados con el procedimiento que se estudiará posteriormente. A continuación, cada uno de ellos:

Razones

De esta manera, se comenzará por decir que las Razones han sido explicadas, por las Matemáticas, como la expresión del cociente existente entre dos números, y que responde a la siguiente forma:

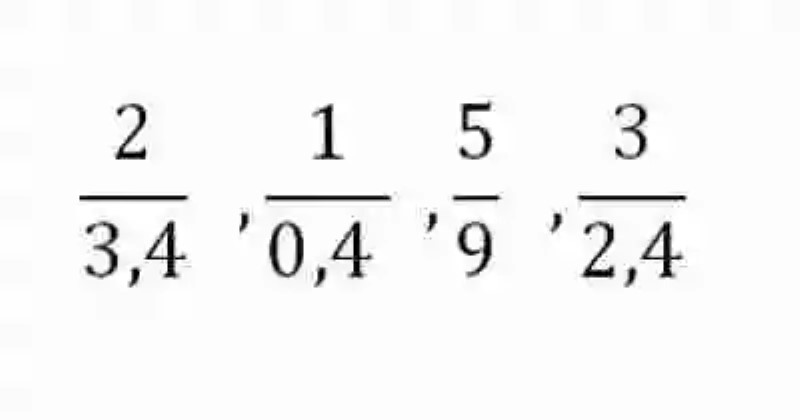
Así mismo, los diferentes autores han señalado la importancia de no confundir las Razones con las Fracciones, pues aun cuando presentan formas parecidas, en realidad refieren y se constituyen de maneras distintas.

En este orden de ideas, las fracciones –constituidas siempre por un numerador y un denominador- deberán entenderse como la expresión de las partes que se toman de una unidad previamente dividida en partes iguales, mientras que las Razones serán vistas como expresiones conformadas por un antecedente y un consecuente, que dan razón del cociente entre dos números, es decir, la cantidad de veces que se encuentra incluido el Divisor dentro del Dividendo. Por igual, las fracciones deberán estar conformadas siempre por números enteros, mientras que en las razones pueden existir, en algunas de sus partes o incluso en ambas, números fraccionarios.

Proporciones

En segunda instancia, será también importante señalar cuál es el concepto de Proporciones, las cuales han sido descritas de manera general como la relación de igualdad que existe entre dos razones, es decir, cuando dos o más razones, independientemente de los valores de sus diferentes partes, conducen al mismo cociente, o expresan el mismo cociente. Por ejemplo, si se tuvieran las siguientes razones:

Pese a tener diferentes valores sus respectivos antecedentes y consecuentes, en realidad son iguales, o en otras palabras proporcionales, puesto que al resolverse, ambas arrojan como cociente el número 2.

No obstante, esta no es la única forma en que las Matemáticas logran comprobar la proporcionalidad de dos razones, ya que por lo general se basan también en una de las leyes de la proporción, la cual dicta que siempre que dos razones son proporcionales, el producto del antecedente de la primera por el consecuente de la segunda –llamados extremos- debe ser igual al producto del consecuente de la primera por el antecedente de la segunda razón, elementos que a su vez se denominan medios:

Esta ley es bastante útil en caso de desconocerse algunos de los factores de dos razones que resultaran proporcionales, puesto que bastaría con resolver el producto de los que sí se conocen, y dividirlo entre el otro factor. Por ejemplo:

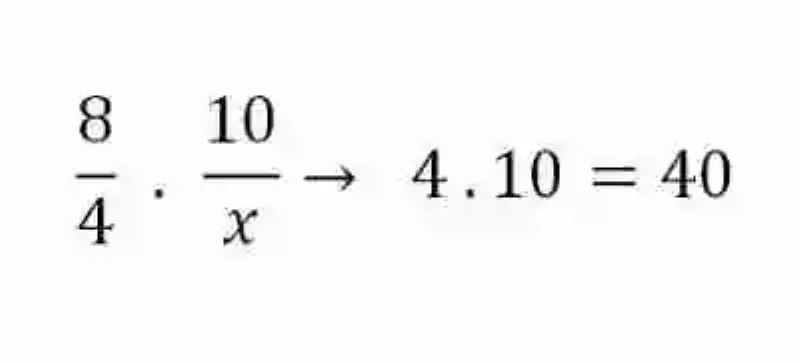
Si se tuviese la siguiente proporción, en la cual se desconociera uno de los elementos, y se quisiera resolver cuál es el número que corresponde, se debería proceder multiplicando los dos que se conocen:

Al hacerlo, se obtiene como producto 40. Este número deberá ser dividido entre 8, que es el único elemento de los extremos que se conocen:

40 : 8 = 5

El resultado es el otro elemento de los extremos que no se conocía, y que es necesario para establecer la proporcionalidad entre estas dos razones:

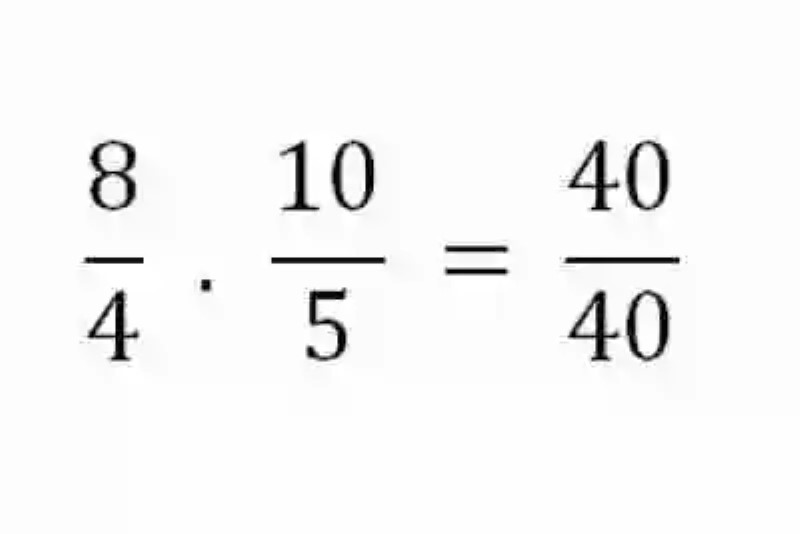
Magnitudes directamente proporcionales

Por último, será también necesario revisar el concepto de Magnitudes directamente proporcionales. Para esto, se deberá comenzar por decir que las Matemáticas han señalado las Magnitudes como aquellos conjuntos de elementos, que cuentan con la propiedad de sumarse, compararse u ordenarse.

Con respecto a las Magnitudes que pueden ser señaladas como directamente proporcionales, estas serán explicadas como aquellas magnitudes en donde siempre que una de ellas se multiplique por un número específico, la otra también quedará multiplicada por el mismo número.

Por ejemplo, si se entrara en una tienda, queriendo comprar un metro de tela y la vendedora informara que esta cantidad de material vale 5 dólares, entonces a la hora de querer saber cuál es el precio de tres metros de esta tela, se deberá simplemente multiplicar el precio por el número de metros, puesto que la cantidad de tela es directamente proporcional con su precio:

1 metro de tela → 5 dólares
3 metros de tela → 15 dólares

Esta relación de proporcionalidad directa entre estas dos magnitudes cuenta también con las propiedades de conformar razones proporcionales, al tiempo que forman serie de razones iguales

Regla de tres simple directa

Una vez se han explicado estos conceptos, puede que sea mucho más sencillo revisar el concepto de Regla de tres simple directa, la cual ha sido descrita como un procedimiento matemático usado para despejar o conocer algunos de los factores que puedan existir entre dos magnitudes directamente proporcionales.

Sin embargo, puede que la mejor forma de entender este procedimiento sea usar un ejemplo, que permita ver de forma concreta en qué consiste, tal como se muestra a continuación:

Suponiendo que se comiencen a producir lazos para cabello, y cada uno de ellos se quiera vender en 4 euros, y se quisiera saber cuál sería el precio en que deberían venderse cuatro lazos, pues entonces se deberá realizar una operación de regla de tres simple directa, lo cual se podrá hacer por ser estas magnitudes directamente proporcionales. Por lo tanto, se tendrá lo siguiente:

1 lazo  →  4 euros
4 lazos →  x

Al plantear el problema, este deberá resolverse tal como  se hace con las razones proporcionales, es decir, multiplicando los medios y dividiendo el resultado entre el único elemento de los extremos que se conoce:

Teniendo este producto, se considera despejada la operación. Si se deseara comprobar que se ha obtenido el resultado correcto, entonces se deberá buscar el producto de los extremos y los medios, lo cual debe originar el mismo resultado. Por ende, se considera despejada la Regla de tres simple directa:

1 lazo  →  4 euros
4 lazos →  16 euros

Imagen: pixabay.com