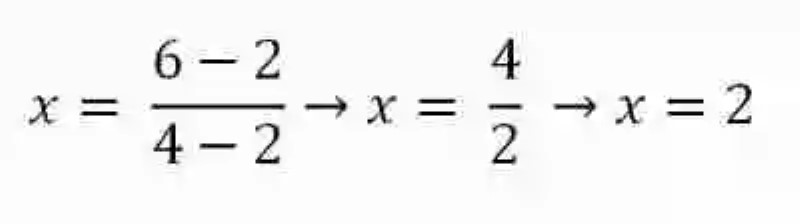Previo a abordar una explicación sobre la forma correcta de resolver una ecuación de primer grado, del tipo ax + b = cx + d, se revisarán brevemente algunos conceptos, que de seguro permitirán entender este procedimiento matemático dentro de su justo contexto matemático.
Definiciones fundamentales
En este sentido, puede que también resulte de provecho delimitar esta revisión teórica a tres definiciones específicas: Igualdades, Ecuaciones y Ecuaciones de primer grado, por encontrarse directamente relacionadas con el procedimiento que se estudiará posteriormente. A continuación, cada una de estas definiciones:
Igualdades
Por consiguiente, se puede comenzar por decir que las Igualdades han sido explicadas por las distintas fuentes matemáticas como la relación que existe entre dos términos o elementos que pueden considerarse como iguales. Así mismo, la disciplina matemática ha indicado que el signo para expresar esta relación es el signo igual (=).
Además, las igualdades pueden considerarse conformadas por dos distintos miembros, cada uno de los cuales han sido explicados de la siguiente manera:
- Primer término: considerado como el elemento o conjunto de elementos que se disponen de forma anterior al signo igual (=).
- Segundo término: por su lado, el segundo término de la igualdad será entonces el elemento o conjunto de elementos que se encuentran ubicados después del signo igual.
También, las Matemáticas han señalado que pueden identificarse dos distintos tipos de igualdades:
- Igualdades numéricas: cuando los elementos entre los que se sostiene la igualdad se encuentran conformados plenamente por números.
- Igualdades literales: cuando los elementos entre los que se establece la igualdad, además de elementos numérico, también cuentan con la presencia de elementos literales.
En segunda instancia, también será menester detenerse un momento en el concepto de Ecuaciones, las cuales han sido explicadas entonces como aquellas igualdades literales, que se caracterizan en la posibilidad de su elemento literal de sólo poder contar con un posible valor, capaz de hacer que la relación de igualdad se cumpla. Un ejemplo de este tipo de igualdades literales será el siguiente:
x – 4 = 6
Suponiendo que se tenga esta ecuación, se deberá probar con hacer que la x asuma distintos valores, a fin de poder comprobar ciertamente si esta relación de igualdad se cumple o no:
3 – 4 = 6 → -1 ≠ 6
5 – 4 = 6 → 1 ≠ 6
9 – 4 = 6 → 5 ≠ 6
10 – 4 = 6 → 6 = 6Al hacerlo, se encuentra entonces que ciertamente la igualdad literal planteada solo logra cumplirse cuando la x asume como valor el número 10. Siendo entonces una igualdad literal en donde solo es posible que la x tenga un valor, se habla entonces de una Ecuación.
Ecuaciones de primer grado
Por último, resultará también beneficioso lanzar luces sobre el concepto de Ecuaciones de primer grado, las cuales han sido explicadas entonces como aquellas igualdades literales, en donde el literal o incógnita solo puede asumir un valor, pues es el único que sirve para que la igualdad permanezca, y en donde además este literal se encuentra elevado a un exponente igual a la unidad.
En caso de que la ecuación presentara varios literales, entonces todos deberían estar elevados a un exponente igual a la unidad.
Resolución de ecuaciones de tipo ax + b = cx + d
Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre la forma adecuada en que debe realizarse la resolución de ecuaciones de primer grado, correspondientes al tipo ax + b = cx + d, procedimiento este que deberá regirse por los siguientes pasos:
1.- Una vez se ha planteado esta operación, y viendo que ambos términos de la ecuación cuentan con una x, entonces se procede a par ambas incógnitas al primer término. Al hacerlo, la x pasa junto al elemento que está multiplicándola, y si tiene un signo positivo, pasa al primer término, o se traspone, asumiendo el signo contrario, es decir, el signo negativo:
ax + b = cx + d → ax – cx + b = d
2.- El siguiente objetivo será entonces aislar las x en el primer término de la ecuación. Para esto, se pasa el elemento que no está acompañando a las x al segundo término, como está sumando, pasa al otro término como negativo:
ax – cx + b = d → ax – cx = d – b
3.- Sucediendo que en el primer término existen dos elementos que se multiplican por x, se procede a reducirlos, a fin de simplificar esta término:
ax – cx = d – b → (a – c)x = d – b
4.- Hecho esto, se procederá entonces a aislar a x en un solo término, por lo que se deberán pasar los elementos diferentes a ella del primer término al segundo. Como estos se encuentran multiplicando, pasan entonces al segundo término dividiendo:
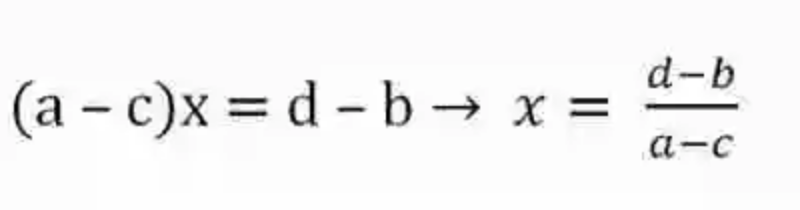
5.- El paso siguiente será resolver la operación planteada, puesto que esto significa descubrir o determinar el valor final de x.
6.- Finalmente, se podrá comprobar si se ha hallado la solución correcta. Para esto, bastará con sustituir en la igualdad literal original la x por el valor determinado, y resolver las operaciones planteadas, a fin de comprobar la igualdad.
Ejemplo
Sin embargo, puede que la forma más eficiente de completar esta explicación sea a través de la exposición de un ejemplo concreto que permita ver cómo se deben resolver en la práctica este tipo de ecuaciones. A continuación, la siguiente operación:
4x + 2 = 2x + 6
4x – 2x = 6 – 2
(4 – 2)x = 6 -2
Comprobación:
4x + 2 = 2x + 6
4.2 + 2 = 2.2 + 6
8 + 2 = 4 + 6
10 = 10
Imagen: pixabay.com
El pensante.com (enero 7, 2019). Resolución de ecuaciones del tipo ax + b = cx + d. Recuperado de https://elpensante.com/resolucion-de-ecuaciones-del-tipo-ax-b-cx-d/