
Tabla de contenido
Antes de avanzar en una explicación sobre la forma correcta en que debe abordarse el segundo caso de la Regla de compañía, es decir, en donde los socios de una empresa aportan igual cantidad de capital, pero cuentan con tiempos de inversión distintos, puede que sea recomendable revisar de forma breve algunas definiciones, que de seguro permitirán entender este caso en su justo contexto matemático.
Definiciones fundamentales
En este sentido, puede que quizás también sea de provecho delimitar esta revisión teórica a cuatro nociones específicas: Razones, Proporciones, Repartos directamente proporcionales y Regla de compañía, los cuales se tendrán en cuenta por encontrarse directamente relacionados con el caso de la Regla de compañía, que se estudiará posteriormente. A continuación, cada una de estas definiciones:
Razones
De esta manera, se comenzará por decir que las Razones han sido explicadas por las Matemáticas como una expresión, que sirve para dar cuenta de un cociente entre dos números, es decir, que las razones expresan cuántas veces se encuentra contenido un Divisor dentro de un Dividendo. Algunos ejemplos de razones pueden ser los siguientes:
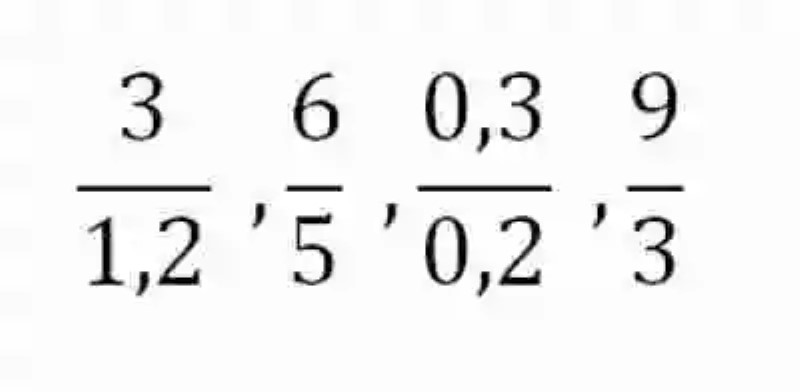
Así mismo, en este punto es importante advertir sobre la necesidad que existe de no confundir el concepto de Fracciones con el de Razones, en tanto que además de estar constituidas por elementos diferentes, cada una de ellas conforma expresiones de realidades matemáticas distintas.
En este sentido, se tendrá que las Fracciones –conformadas por el numerador y el denominador- dan cuenta de cuál es el número de partes que se han tomado de una unidad que se encuentra dividida en partes iguales. Por su lado, las Razones –constituidas por el Antecedente y el Consecuente- se dedican entonces a señalar cuál es el cociente entre dos números.
Otra importante diferencia entre estas dos expresiones matemáticas será que mientras las Fracciones deben tener sus elementos conformados necesariamente por números enteros, las Razones por su parte pueden estar conformadas tanto por números enteros como decimales.
Proporción
En segunda instancia, también será necesario tomar un momento para lanzar luces sobre el concepto de Proporción, el cual es tenido entonces por las Matemáticas como la relación de igualdad que existe entre dos razones, es decir, que la Proporción básicamente es la relación que surge entre dos razones que expresan el mismo exponente. Por ejemplo, si se tuvieran las dos razones siguientes:
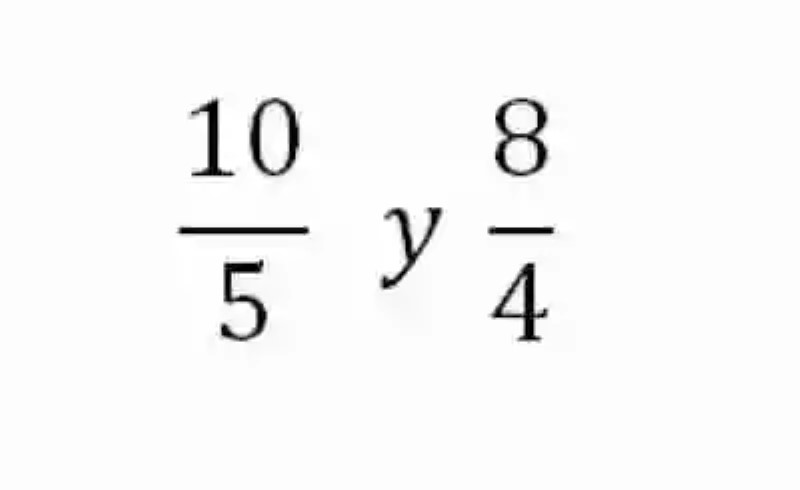
Se podría ver cómo estas expresiones, pese a tener cada uno de sus elementos conformado por valores distintos pueden ser consideradas como razones iguales, en tanto que ambas conducen al cociente 2. Por ende, estas razones son tenidas como proporcionales.
Sin embargo, esta no es la única forma de determinar si dos razones son o no iguales. Otra de los métodos concebidos por las Matemáticas para este fin es aquel en donde se procede a multiplicar entre ellos los extremos de las razones (es decir, el antecedente de la primera expresión, así como el consecuente de la segunda) al igual que los medios (el consecuente de la primera razón y el antecedente de la segunda expresión). Si las razones son proporcionales, estas multiplicaciones deben arrojar el mismo producto:

Esta cualidad de las razones proporcionales, se conoce como una de las dos principales leyes de la proporcionalidad, y es sumamente útil a la hora de despejar o conocer algunos de los elementos de las proporciones, pues para esto será necesario solo multiplicar los dos elementos que se conocen de los extremos o de los medios, para proceder posteriormente a dividir este producto entre el único elemento que se conoce del ámbito de la proporcionalidad que desea conocerse:
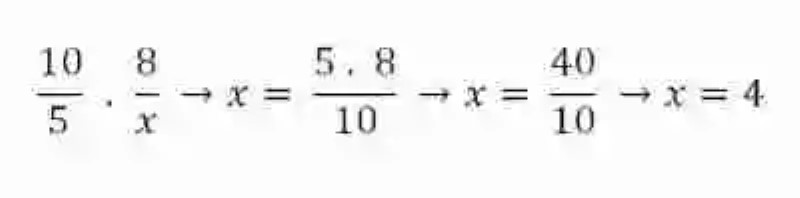
Reparto directamente proporcional
Así también, será necesario tomar un momento para detenerse sobre el concepto de Reparto directamente proporcional, el cual será entendido como el procedimiento matemático dirigido a determinar cuál es la manera correcta en que debe repartirse, de forma proporcional, una cantidad entre elementos o números específicos.
Este procedimiento resulta bastante útil tanto en la vida académica, como en la cotidiana. Por ejemplo, podría ser usada para conocer cuál es la paga específica que le corresponde a cada empleado, que haya participado en un trabajo para el cuál hubo una paga general. Sin embargo, este tipo de procedimiento es mejor explicarlo con un ejercicio concreto, tal como el que se muestra a continuación:
En una carpintería se fabricaron 6 mesas, por las cuales se pagaron un total de 600 euros. En este trabajo participaron tres carpinteros, quienes elaboraron cierta cantidad respectiva de mesas: Juan hizo 3, Pedro tan solo 1 y Mauricio 2 de ellas. ¿Cómo saber cuánto dinero debe recibir cada uno de ellos por su trabajo realizado?
Al momento de iniciar la resolución de este ejercicio, puede que lo mejor sea empezar por expresar la información que se tiene:
Juan: 3 mesas
Pedro: 1 mesa
Mauricio: 2 mesasTotal de mesas: 6 mesas
Total de paga: 600 eurosLuego de saber cuáles son los datos con los que se cuenta, se escogerá el método de la reducción a la unidad, para descubrir cuál es el valor unitario de cada mesa:
Al saber que cada una de las mesas cuesta 100 euros, ya se podrá determinar cuáles son las pagas individuales que le corresponde a cada uno de los carpinteros, y para lo que simplemente será necesario multiplicar el valor de cada mesa por el número de mesas que fabricó cada uno:
Juan: 3 x 100 = 300 euros
Pedro: 1 x 100 = 100 euros
Mauricio: 2 x 100 = 200 euros
Regla de compañía
Por último, será necesario revisar el concepto de Regla de compañía, la cual ha sido explicada de forma general como el método o procedimiento que se realiza para determinar la forma proporcional en que deben repartirse las ganancias o las pérdidas de una empresa, entre cada uno de los socios que han participado de ellos, según el capital que han aportado, o el tiempo que han estado dentro del negocio.
Por lo general, esta repartición se hace según los reglamentos o estatutos legales en base a los cuales se ha creado la empresa. Sin embargo, también puede aplicarse el método de Regla de compañía.
Segundo caso: capitales iguales, tiempos de inversión distintos
Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre lo que matemáticamente se conoce como el Segundo caso de la Regla de compañía, el cual tratará de establecer cómo debe repartirse proporcionalmente las ganancias o pérdidas de una compañía, en donde los socios han invertido igual cantidad de capitales, pero han permanecido tiempos diferentes en la inversión.
No obstante, puede que la mejor forma de cerrar una explicación sobre el Segundo caso de la Regla de la compañía, sea exponer un ejemplo concreto, que permita ver de forma práctica cómo abordar este tipo de ejercicios, tal como se puede ver a continuación:
Suponiendo que en una empresa existen dos socios que han invertido cada uno por su lado unos 500 euros, pero el primero estuvo en el negocio 6 meses, y el segundo tan solo 5 meses, y que durante su participación se produjo una ganancia de 1200 euros, ¿de qué forma se debe repartir esta ganancia?
Lo primero que deberá hacerse antes de comenzar a resolver este ejercicio será exponer la información con la que se cuenta:
Ganancia total: 1200 euros
Suma de tiempos: 6 + 5= 11 mesesAsí mismo, se deberá construir una razón entre la cantidad de la ganancia total, la cual se establecerá como el antecedente, mientras el consecuente será establecido en cuanto a la suma de los meses que cada socio ha estado en el negocio:
Por último, a la hora de querer saber cuál es la ganancia de cada socio, será necesario entonces multiplicar esta razón, construida entre el total de la ganancia y el número de meses, por el tiempo de participación de cada uno de los socios:
Otros casos de la Regla de la compañía
De igual forma, en este procedimiento matemático pueden encontrarse otros dos casos, los cuales se encontrarán constituidos por los siguientes argumentos:
Primer caso: capitales distintos, tiempo de inversión iguales
Este método será usado para saber cuál es la ganancia que le corresponde a cada uno de los socios que hayan participado en una empresa, a la cual hayan aportado capitales diferentes, pero que hayan permanecido tiempos iguales en la empresa. Para determinar este valor, será necesario seguir los pasos que se nombran a continuación:
- Establecer una razón entre la ganancia total de la empresa y la suma de cada uno de los capitales aportados por los socios entres los que se deben repartir las ganancias.
- A la hora de establecer cuál es la ganancia que le corresponde a cada socio, será necesario multiplicar la razón obtenida por el capital que el socio ha aportado.
Tercer caso: capitales distintos, tiempos de inversión distintos
Por otro lado, la Regla de la compañía podrá usarse también para establecer la ganancia que le corresponde a cada socio de una compañía, cuando estos han aportado capitales diferentes, y así mismo han permanecido durante tiempos diferentes en la empresa. En este tipo de caso, se deberá proceder de la siguiente forma:
- Se establece una multiplicación entre el capital aportado y la cantidad de tiempo que ha permanecido en la empresa.
- Crear una razón entre la cantidad total de ganancia total y la suma de los productos entre el capital aportado y el tiempo de participación de cada socio.
- Multiplicar esta razón por el producto entre el capital aportado y el tiempo de participación de cada socio.
Imagen: pixabay.com
El pensante.com (noviembre 6, 2018). Segundo caso de la Regla de compañía (Matemáticas / Proporcionalidad directa). Recuperado de https://elpensante.com/segundo-caso-de-la-regla-de-compania-matematicas-proporcionalidad-directa/


