Semejanzas (figuras geométricas)

Definiciones fundamentales

Por consiguiente, se tomará también la decisión de delimitar esta revisión teórica a tres nociones específicas: Polígonos, Lados y Ángulos, por encontrarse directamente vinculadas a la relación geométrica, que se estudiará posteriormente. A continuación, cada una de estas definiciones:

Polígono

De esta manera, podrá comenzarse a decir que los Polígonos han sido explicados figuras geométricas, planas y bidimensionales, las cuales cuentan tan solo con las dimensiones de Alto y Ancho, es decir, que en ellas no se puede encontrar la tercera dimensión de la profundidad.

Así mismo, las Matemáticas han señalado que los Polígonos se caracterizan también por ser figuras geométricas, completamente cerradas, gracias a la unión de puntos que protagonizan los distintos segmentos de recta que las delimitan.

De igual forma, la Geometría ha señalado que los Polígonos tienen igualmente como rasgo el tener todos sus lados rectos, al tiempo que se distinguen también por tener lados, ángulos, vértices y diagonales.

Lados

En segunda instancia, será también necesario abordar una explicación sobre los Lados, los cuales han sido explicados, de forma general, como uno de los cuatro atributos con los que cuentan las figuras geométricas, en especial, los polígonos.

De igual forma, la Geometría ha señalado que los Lados pueden ser descritos como segmentos de recta, que unen sus puntos en determinados momentos, delimitando un espacio geométrico, y constituyendo así un polígono. Dependiendo del número de lados, se clasificarán los polígonos.

Ángulos

Por último, también se lanzarán luces sobre el concepto de Ángulos, los cuales han sido explicados como otro de los atributos que se pueden encontrar en los polígonos, junto a los Lados, vértices y diagonales.

De forma mucho más específica, los Ángulos pueden ser descritos como el espacio geométrico delimitado por dos segmentos de recta, que se unen en un punto específico, delimitando un espacio geométrico, y creando un vértice. Los ángulos se distinguen por tener una amplitud, que es medida en grados sexagesimales.

Semejanzas

Toda vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre las Semejanzas, las cuales han sido explicadas como aquellas figuras geométricas –o polígonos- que coinciden plenamente en sus formas, pese a tener diferencias en cuanto a sus tamaños respectivos. Un ejemplo de figuras semejantes podría ser el siguiente:

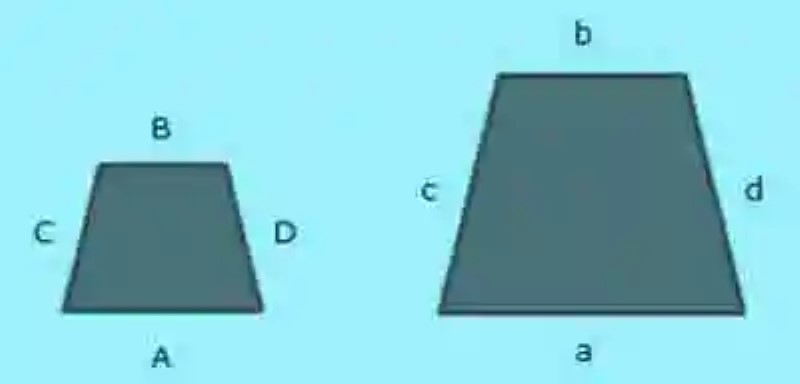
Si se toman estas figuras geométricas, o polígonos, podrán considerarse semejantes, puesto que tienen dos características básicas:

1.- En primer lugar sus lados son proporcionales, esto quiere decir que la Razón de semejanza de los lados horizontales y verticales de cada figura es igual.

2.- Así mismo, las figuras semejantes se caracterizan por tener los mismos ángulos, es decir, que los ángulos que contiene presentan igual amplitud.

Razón de semejanza

Por otro lado, será prudente también pasar revista sobre el concepto de Razón de semejanza, el cual ha sido explicado como una medida que sirve para determinar la proporción entre los lados de dos o más polígonos.

En este orden de ideas, las distintas fuentes han señalado que siempre que se quiera determinar la Razón de semejanza entre dos o más figuras, se deberán seguir los pasos que se mencionan a continuación:

1.- Se enumeran los lados de las figuras, procedimiento que se realiza bautizando los lados con letras. Para figuras que se sospeche que son semejantes, los lados que cuenten con la misma orientación serán bautizados con la misma letra, solo que unos lo harán con letras mayúsculas, y otros con letras minúsculas:

2.- No obstante, también podrá colocarse a cada uno de los lados que conforman las figuras semejantes la medida que presenta.

3.- Se toma entonces las medidas del lado horizontal de la figura 1 y se divide entre la medida del lado horizontal, que le resulta equivalente, en la figura 2.

4.- Se procede de igual forma con los lados verticales, es decir, se toma la medida del lado vertical de la figura 1, y se divide entre la medida del lado vertical de la figura 2.

5.- Ambos cocientes deben ser iguales, lo cual comprueba que las figuras son semejantes.

6.- El cociente que se ha obtenido en ambas divisiones es entendido como Razón de semejanza, la cual es posible sólo si los lados resultan totalmente proporcionales entre ellos.

Ejemplo de cómo se determina la Razón de semejanza

Empero, quizás la forma más eficiente de completar una explicación sobre la Semejanza en las figuras geométricas, y cómo se determina la Razón de semejanza sea revisando de forma breve un ejemplo, que permita ver de forma concreta cómo se debe proceder. A continuación, el siguiente ejercicio:

Suponiendo que se tengan dos rectángulos, determinar si son figuras geométricas semejantes, y de serlo calcular la Razón de semejanza:

Lo primero que se hará será observar las figuras dadas, al hacerlo se puede determinar que las dos son rectángulos, pero de diferentes tamaños. Por lo tanto, coincidiendo en cuanto a sus formas, número de lados y ángulos, entonces ciertamente son Figuras geométricas semejantes.

En este sentido, también se podrá determinar la Razón de semejanza entre sus lados proporcionales:

Razón de semejanza de los lados horizontales → 2 : 3 = 0,66
Razón de semejanza de los lados verticales → 1 : 1,5 = 0,66

La Razón de semejanza de estas figuras es 0,66

Imagen: pixabay.com