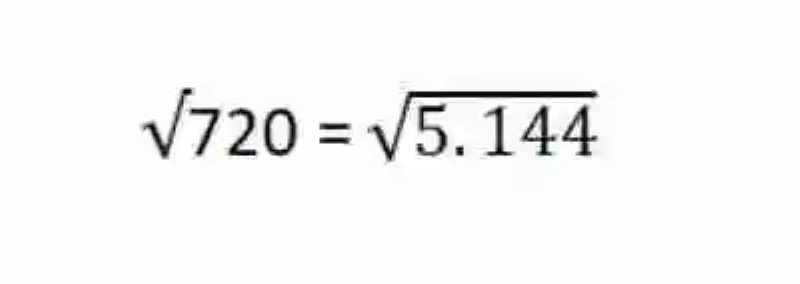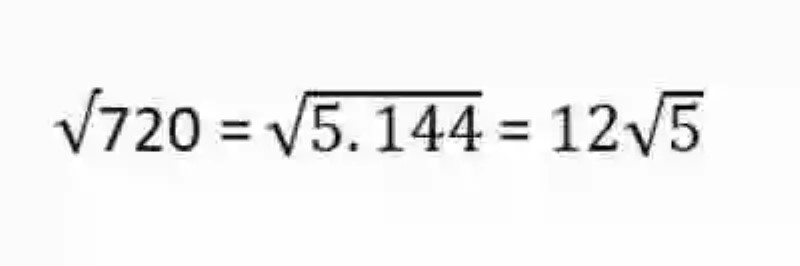Simplificación de raíces

La Radicación

De esta manera, se puede comenzar por decir que las Matemáticas han concebido la Radicación como una operación que sucede entre dos números que tratan de determinar un tercer número, que tenga la propiedad de multiplicarse a sí mismo tantas veces como indique uno de los números involucrados, dando como resultado el otro número participante de la operación, de ahí que algunos autores hayan expresado que la Radicación puede ser vista también como una forma inversa de Potenciación.

Descomposición de raíces

Por su parte, la Descomposición de raíces es vista como el procedimiento matemático por medio del cual se busca que un elemento o el radicando completo puedan ser extraído de la raíz. Si se trata de una raíz exacta, el radicando o el número podrán salir de forma exacta, si es una raíz entera, se deberá descomponer el radicando en factores, y sacar de la raíz, aquellos que se puedan. El objetivo de esta operación es expresar la raíz de forma simplificada.

Factorización de raíces en números primos

Así también, la Factorización de raíces en números primos será vista entonces como otro de los procedimientos matemáticos que permitirán la simplificación de la raíz. En consecuencia, esta operación es vista como una técnica matemática en donde el radicando se descompone en factores, constituidos por números primos, entre los cuales se establece una operación de multiplicación, a fin de dar con la forma más básica y simple en la que pueda ser expresada la raíz.

Simplificación de raíces

Teniendo presente estas definiciones, se podrá concluir entonces que la Simplificación de raíces es vista un método o procedimiento aplicados con el propósito de determinar cuál es la forma más simple en la que pueda expresarse una raíz, lo cual pasa necesariamente por su descomposición o factorización.

Sin embargo, no está demás observar cómo se llevan a cabo cada uno de estos métodos, tal como se muestra seguidamente:

Simplificación por descomposición de raíces

En la descomposición, se hace necesario entonces descomponer el radicando en factores, cada uno de los cuales pueda ser extraído de la raíz, lo cual se lleva a cabo, determinando cuál es el número que elevado al índice, es capaz de ser equivalente al radicando, a fin de obtener la forma más simple en que pueda ser expresada una operación. Un ejemplo de este método podría ser el siguiente:

Descomponer la siguiente raíz: √720

1.- Al tratar de extraer el radicando, se determinará que este no cuenta con una raíz exacta, por lo que es necesario descomponerlo entre los factores más básicos, que puedan después salir de la raíz:

2.- Al hacerlo, se consigue que el factor 144 al ser multiplicado por 5, da como resultado 720, pero a su vez puede ser extraído de la raíz:

3.- Si se quisiera comprobar el resultado, sería necesario simplemente optar por la composición de la raíz, elevando al cuadrado el 12, para que pudiera volver a ser un radicando, y multiplicándolo por 5:

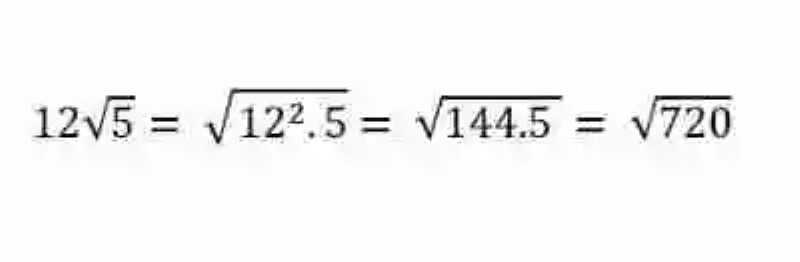
Simplificación por Factorización de raíces

En cambio, si la operación de Simplificación de raíces quiere llevarse a cabo por medio de la Factorización, se deberán seguir los pasos que se muestran en el siguiente ejemplo:

Simplificar por medio de la Factorización de raíces en números primos la siguiente raíz: √720

1.-En primero lugar, se deberá comenzar a dividir el radicando entre los número primos más básicos, siempre que sea una división exacta. En caso de que no se pueda seguir dividiendo por el número por el que se ha comenzado, se puede usar otro número primo de distintos valor:

2.- Acto seguido, se expresarán los distintos factores dentro de la raíz. En caso de que uno de ellos se repita, deberá ser escrito como potencia, siendo el número la base, y el exponente el número de veces que se repite:

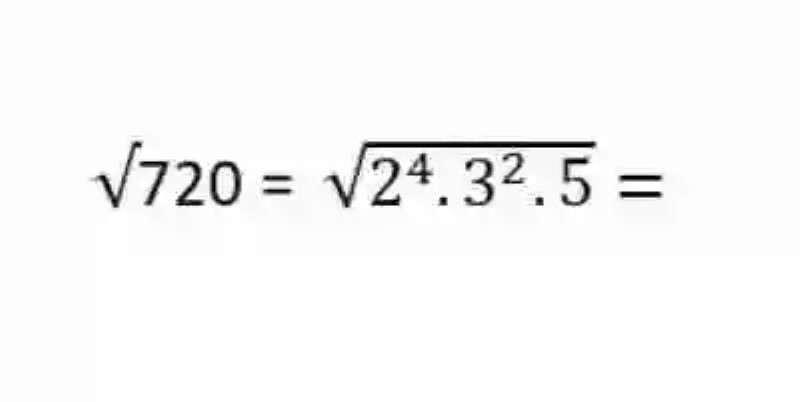
3.- Así mismo, se buscará entonces extraer cada uno de los factores en los que ha podido factorizar la raíz. Para esto, se dividirán los exponentes entre el índice de la raíz, siempre que sea divisible entre 2, que es el índice de la raíz cuadrada:

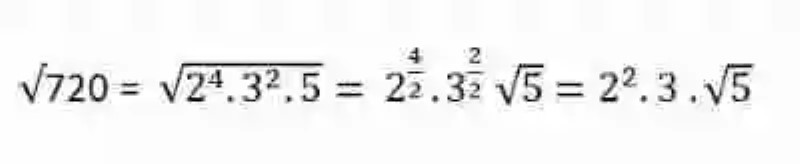
4.- Se resuelven las potencias y las operaciones de multiplicación:

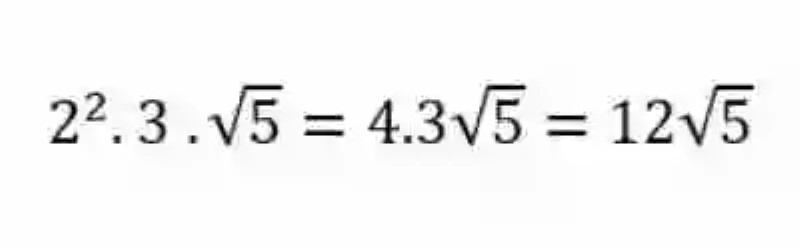
5.- Se interpretará este como el resultado de la operación:

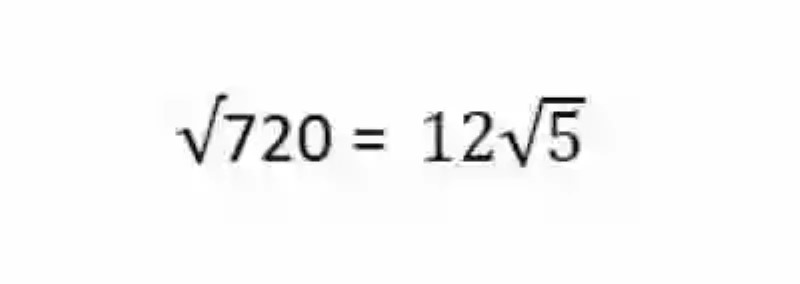
6.- Hecho esto, se puede comprobar que la operación ha sido exitosa, a través de la composición de raíces, para lo cual se incorporará el número fuera de la raíz, nuevamente como radicando, elevándolo al índice de la raíz, y multiplicándolo por el número que ha permanecido dentro de esta:

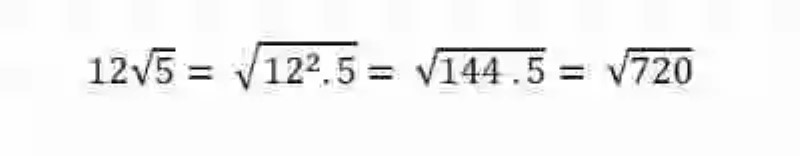
Imagen: pixabay.com