
Antes de entrar a definir de qué se trata la suma de polinomios, así como las distintas operaciones relacionadas, resulta pertinente recordar la propia definición de Polinomios, a fin de poder entender esta operación en su contexto preciso.
Definición de Polinomios
De esta forma, viene bien a recordar que el Álgebra elemental define el Polinomio como una expresión algebraica, compuesta por una suma finita de monomios, los cuales deben cumplir con la principal característica de contar con variables que se encuentren elevadas a exponentes, conformados por números enteros positivos, requisito indispensable para que la suma de monomios pueda ser considerada un polinomio. Así mismo, a pesar de que la definición algebraica de polinomios indica que debe ser una suma de monomios, entre estos términos algebraicos también se tiene en cuenta como posible operaciones de suma y multiplicación, quedando descartada dentro de los polinomios, la operación de división.
Elementos del polinomio
Con respecto a los distintos elementos que conforman el Polinomio, el Álgebra indica que esta expresión algebraica está compuesta esencialmente por monomios. Empero, se pueden distinguir cuatro elementos fundamentales, cada uno de los cuales puede definirse a su vez de la siguiente manera:
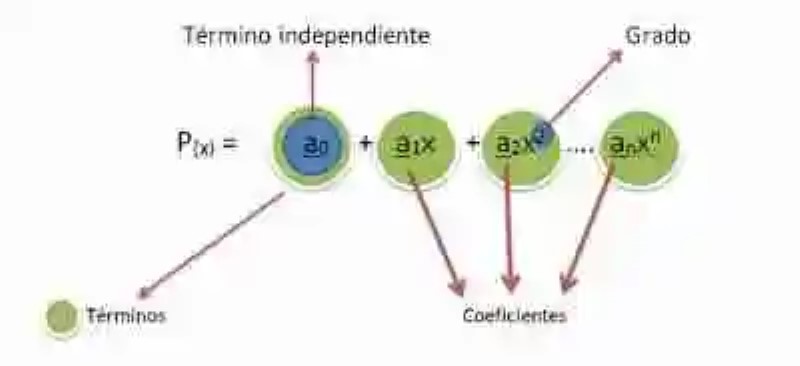
- Términos: cada uno de los sumandos del polinomio.
- Términos independientes: elementos numéricos que no cuentan con presencia de variable.
- Coeficientes: elementos numéricos que acompañan a la variable.
- Grado: elemento determinado por el grado de mayor valor que pueda determinarse en los monomios que conforman el polinomio.
Suma de polinomios
Entre las distintas operaciones que pueden darse entre y en relación con los polinomios, se encuentra la de la suma de polinomios, la cual consiste en sumar cada uno de los términos semejantes (es decir, que posean igual variable y grado) a fin de poder tener una sola expresión algebraica. No obstante, el Álgebra contempla dos posibles métodos, con los cuales llevar a cabo la suma de polinomios:
Método 1
La primera opción, cuando se plantea la suma de polinomios, consiste en -una vez ordenados ambos polinomios- anotarlos como una sola expresión algebraica ordenada, para posteriormente entrar a sumar los coeficientes de aquellos términos que coincidan en cuanto a sus variables y exponentes. Para ilustrar esta definición, lo mejor será usar el siguiente ejemplo:
Dados los siguientes polinomios:
P(xy)= 5x2y3 – 4 – 5x2 – 5xy – 5 + x3x4
Q(xy)= -3xy + 6x2y3 – 4x2 – 8x3y4 – 3 + 3
El primer paso a seguir será organizar cada uno de los polinomios planteados, a fin de poder precisar mucho mejor los términos semejantes. Al tratarse de polinomios de más de una variable, el ordenamiento se hará en base a la letra ordenatriz escogida, así como a la disposición que se desee. En este caso, la ordenatriz será la variable x, y el orden descendente, por lo que se buscará entonces el máximo exponente de esta variable, para ordenar los términos de cada polinomio a partir de ella:
P(xy)= x3y4 + 5x2y3– 5x2 – 5xy – 4– 5
Q(xy)= – 8x3y4 + 6x2y3– 4x2 – 3xy – 3 + 3
Hecho esto, se debe buscar entonces la forma de convertir ambos polinomios en una sola expresión algebraica:
P(xy) + Q(xy)= x3y4–8x3y4+5x2y3+ 6x2y3– 5x2– 4x2–5xy–3xy– 4–3 –5 +3
Así mismo, se procederá entonces a sumar los coeficientes de los términos semejantes, a fin de culminar la suma de polinomios:
P+Q(=(x3y4–8x3y4)+(5x2y3+ 6x2y3)+(-5x2–4x2)+(-5xy–3xy)–4-3–5 +3
P(xy) + Q(xy)= (1–8)x3y4+ (5+ 6)x2y3 + (-5-4)x2+(-5–3)xy– 4–3 –5 +3
P(xy) + Q(xy)= -7x3y4+ 11x2y3 – 9x2 – 8xy – 4–3 –5 +3
Así mismo, se resolverán los términos independientes según la Ley de signos:
– 4–3 –5 +3
números positivos: 3
números negativos: -4-3-5= -123-12=-9
Por ende, el resultado de la suma de estos polinomios, será entonces:
P(xy) + Q(xy)= -7x3y4+ 11x2y3 – 9x2 – 8xy – 9
Método 2
No obstante, el Álgebra elemental también concibe un segundo método con el cual se puede realizar la suma de polinomios, la cual consiste en ordenar los polinomios que participarán en la operación, a fin de poder ver de una forma mucho más gráfica cuáles son los términos semejantes que deben sumarse. Un ejemplo de esto, se puede ver usando los mismos polinomios que en el método anterior:
P(xy)= 5x2y3 – 4 – 5x2 – 5xy – 5 + x3x4
Q(xy)= -3xy + 6x2y3 – 4x2 – 8x3y4 – 3 + 3
De esta forma, el primer paso que debe seguirse será el de ordenar cada uno de esto polinomios, al tratarse de polinomios de más de una variable, se decidirá que la letra ordenatriz sea la x, así como que el orden sea ascendente. Identificado el 4 como el mayor grado, el ordenamiento se hará a partir de esta variable:
P(xy)= x3x4 + 5x2y3 – 5x2 – 5xy – 4– 5
Q(xy)= – 8x3y4 + 6x2y3 – 4x2 -3xy– 3 + 3
Hecho esto, se deben colocar uno sobre otro, cuidando de dejar un espacio vacío en caso de que el término correspondiente a la sucesión ininterrumpida falte, es decir, que no se trate de polinomios completos.
x3y4 + 5x2y3 – 5x2 – 5xy – 9
– 8x3y4 + 6x2y3 – 4x2 – 3xy +0
________________________-7x3y4+ 11x2y3 – 9x2 – 8xy – 9
Al comparar los resultados de ambos métodos, se puede observar cómo son iguales:
Método 1: P(xy) + Q(xy)= -7x3y4+ 11x2y3 – 9x2 – 8xy – 9
Método 2: P(xy) + Q(xy)= -7x3y4+ 11x2y3 – 9x2 – 8xy- 9
Imagen: flickr.com
El pensante.com (abril 24, 2017). Suma de polinomios. Recuperado de https://elpensante.com/suma-de-polinomios/