
Antes de abordar una explicación sobre la Tabla de valores de una función, así como el modo de completarla, se revisarán algunas definiciones, que de seguro permitirán entender este procedimiento dentro de su justo contexto matemático.
Definiciones fundamentales
De esta manera, se decidirá igualmente delimitar esta revisión teórica a tres nociones específicas: Conjuntos, Correspondencia y Función, por encontrarse directamente relacionadas con el procedimiento matemático, que se estudiará posteriormente. A continuación, cada una de las siguientes definiciones:
Los conjuntos
Por consiguiente, podrá comenzarse por decir que los Conjuntos han sido explicados por las Matemáticas como un objeto, conformado en base a la reunión de una serie de elementos, que pueden ser identificados como pertenecientes a la misma especie. Por ende, la disciplina matemática, ha señalado que los Conjuntos pueden ser también comprendidos como colecciones abstractas y homogéneas.
Así también, los diversos autores han señalado que los Conjuntos contarán con la característica de ser constituidos por elementos, que cuentan con la capacidad de determinarlos, de forma única y exclusiva. Con respecto a la manera en que estas colecciones deben expresarse, las distintas fuentes señalan que los conjuntos deberán ser siempre denominados a través de letras mayúsculas, mientras que sus elementos deberán presentarse como una enumeración, separados por comas y entre signos de llaves: { }.
Correspondencia
Por otro lado, se precisará también lanzar luces sobre el concepto de Correspondencia, el cual ha sido explicado como una relación matemática, que ocurre entre dos conjuntos, toda vez que uno, algunos o todos los elementos de una de las colecciones encuentren correspondencia, según un criterio de relación específico, entre los elementos de uno, algunos o todos los elementos del segundo conjunto. Un ejemplo de este tipo de relación sería el siguiente:
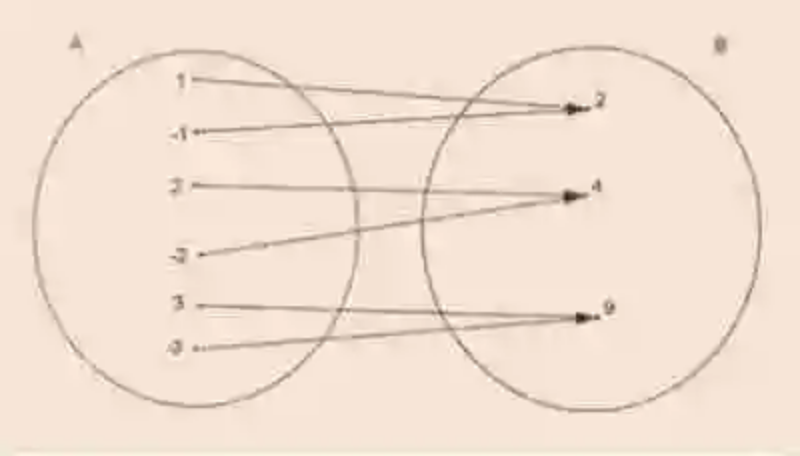
Por otro lado, las Matemáticas han señalado que en toda relación de Correspondencia se pueden encontrar tres distintos conjuntos:
- Conjunto inicial: constituido por los elementos de la colección desde la cual surge la correspondencia, así como las flechas que la señalan. Así mismo, los elementos que conforman este conjunto reciben el nombre de elementos antiimagen, correspondiéndoles además ejercer como primer elemento del par de correspondencia. En el caso del ejemplo usado para ilustras la Correspondencia, el conjunto inicial será el siguiente: A = {1, -1, 2, -2, 3, -3}
- Conjunto final: de igual manera, en la Correspondencia, se encontrará el Conjunto final o de llegada, el cual básicamente se puede definir como la colección en la cual desembocan las flechas que señalan la correspondencia. Los elementos de este conjunto, que participen de la correspondencia, serán denominados por su parte como elementos imagen, teniendo la responsabilidad de ejercer como segundos elementos del par de correspondencia. Este conjunto, en el caso del ejemplo usado, se escribirá de la siguiente manera: B= {2, 4, 9}
- Grafo: finalmente, dentro de los distintos conjuntos que se establecen en la Correspondencia, se encontrará el Grafo, colección conformada en base a los distintos pares de correspondencia, creados entre los elementos del conjunto inicial y los elementos del conjunto final. En el ejemplo usado, el Grado sería el siguiente: G = {(1, 2), (-1,2), (2, 4), (-2, 4), (3, 9), (-3, 9)}
Función
Otro de los conceptos que deben tomarse en cuenta es el de Función, la cual ha sido definida como la relación matemática de correspondencia, que existe entre dos conjuntos, toda vez que los elementos del conjunto final o de llegada sirven de imagen una sola vez a algún elemento del conjunto inicial, es decir, se asumirá que existe una Función cuando los elementos del conjunto de partida, que participan de la correspondencia, cuentan con una sola imagen. Un ejemplo de este tipo de relación será el siguiente:
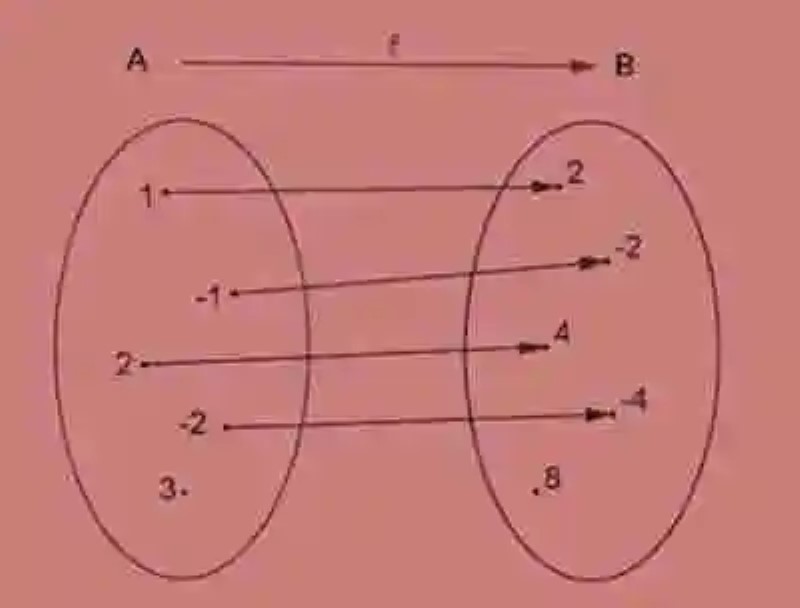
En este ejemplo puede verse cómo los elementos del conjunto A (conjunto inicial) cuentan con tan solo una imagen en el conjunto B (conjunto de llegada) relacionándose en base al criterio de correspondencia (el doble de). Los cual hará que sus variables se expresen también de la siguiente forma:
- Variable independiente: denominada como x, podrá ser ejercida por cualquier valor del conjunto inicial, que participe de la correspondencia.
- Variable dependiente: estas se encontrarán en función de x, y estará conformada por el número que dé como resultado la aplicación de la función. En este caso, y siempre será el doble de x.
Por ende, a la hora de expresar algún valor o variables de esta relación se hará de la siguiente manera:
f (x) = y
Sabiendo entonces que y = 2.x
Tablas de valores de una función
Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre la forma en que deben ser completadas las tablas de valores de una función, la cual puede ser definida como el gráfico en el cual se van anotando los distintos valores que va asumiendo x, y cómo según el criterio de correspondencia se van manifestando en y.
Por ejemplo, si se tuviera la función de x, siendo definida y en base al criterio del cuadrado de, entonces se tendría lo siguiente:
fx(y) → x2
Entonces, x puede tomar como valores a todos los números enteros. Por su parte, y será igual al cuadrado del valor que tome x para cada ocasión. Si se quisiera llenar una tabla de valores deberíanir proponiéndose valores para x, y calculando según el criterio establecido, valores para y:
f (1) = 12 = 1 → f(1) = 1
f (2) = 22 = 4 → f(2) = 4
f (3) = 32 = 9 → f(3) = 9
f (4) = 42 = 16 → f(4) = 16
Obtenidos los valores para x y para y, entonces se procede a llenar la tabla:
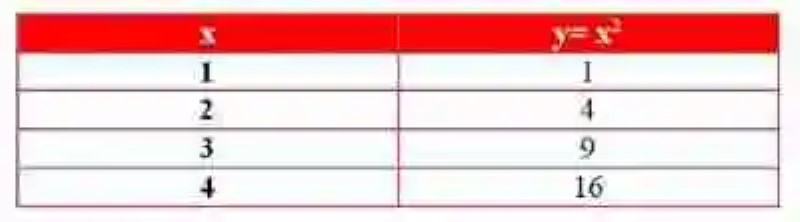
Imagen: pixabay.com
El pensante.com (marzo 14, 2019). Tabla de valores de una función. Recuperado de https://elpensante.com/tabla-de-valores-de-una-funcion/