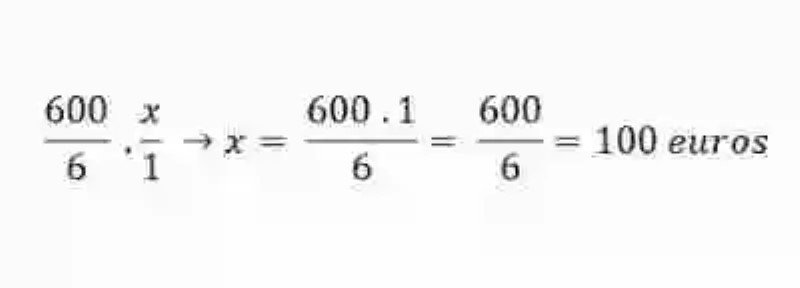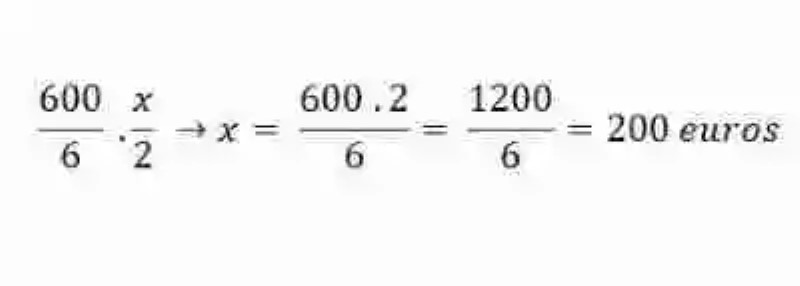Utilizando la regla de tres (problemas de reparto directamente proporcional)

Definiciones fundamentales

En este sentido, puede que también sea necesario delimitar esta explicación a cuatro nociones fundamentales: Razones, Proporciones, Magnitudes directamente proporcionales y Repartos directamente proporcionales, por encontrarse relacionados con el método que se estudiará posteriormente. A continuación, cada uno de ellos:

Razones

Por consiguiente, se tendrá que las Razones han sido explicadas, de forma general, como una expresión matemática, que da cuenta del cociente existente entre dos números, es decir, de la cantidad de veces de un Divisor se encuentra contenido dentro de un Dividendo. A continuación, algunos ejemplos de Razones:

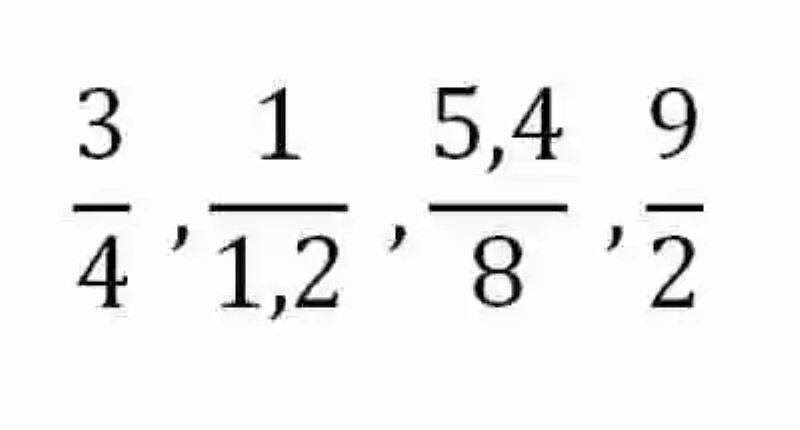
De acuerdo a lo que señalan los distintos autores, en toda Razón se pueden encontrar dos distintos elementos: el Antecedente, el cual cumple con la función de señalar el Dividendo; y el Consecuente, elemento que ejerce las veces de Divisor.

Proporciones

En segunda instancia, también será de provecho lanzar luces sobre el concepto de Proporciones, las cuales han sido explicadas como la relación de igualdad que puede encontrarse entre dos razones. Un ejemplo de proporción ocurre en las dos razones que se ofrecen a continuación:

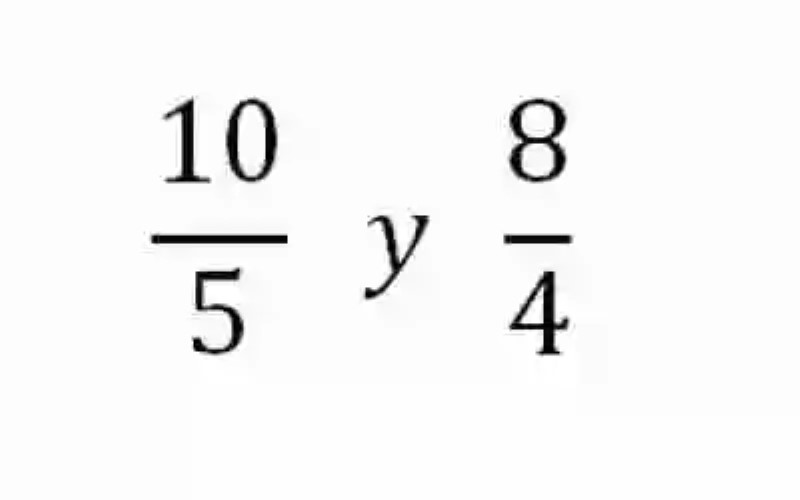
Pese a que todos los elementos de estas razones cuentan con elementos diferentes, ellas pueden ser consideradas como iguales, o proporcionales, en tanto que dan cuenta del mismo cociente, puesto que si se resolvieran las divisiones que ellas plantean, en ambos casos se obtendría un cociente igual a 2.

Sin embargo, este no es el único método que las Matemáticas consideran para determinar la proporción entre dos razones. En este sentido, la disciplina matemática señala que siempre que se quiera establecer la proporcionalidad entre dos razones habrá que recurrir a multiplicar sus extremos –conformado por el antecedente de la primera razón y el consecuente de la segunda- y los medios –constituidos por el consecuente de la primera y el antecedente de la segunda razón- procedimientos que, si las razones son proporcionales, deberían arrojar exacto resultado. Por ejemplo:

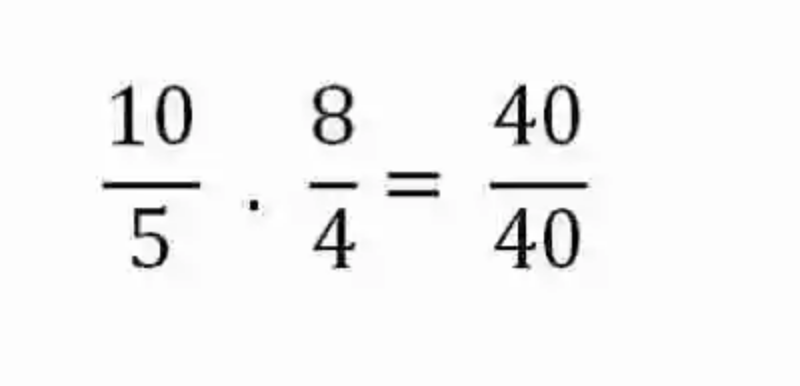
Este procedimiento resulta bastante útil, cuando por ejemplo se desconoce uno de los elementos de dos razones que se saben proporcionales, puesto que para conseguir despejar el número conocido será necesario simplemente el multiplicar los dos elementos conocidos, bien si son los extremos o los medios, y dividirlo entre el único elemento que se conoce de alguno de los dos ámbitos de la proporción, tal como puede verse en el caso que se presenta a continuación:

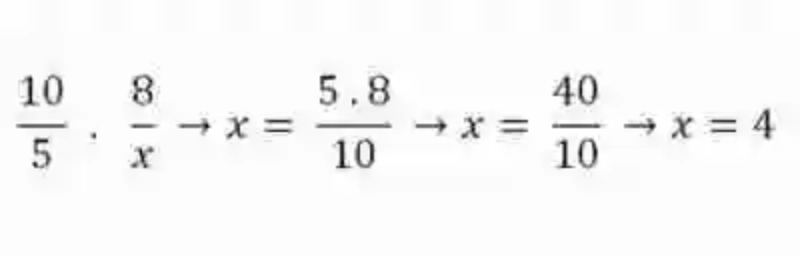
Magnitudes directamente proporcionales

Así también, resultará conveniente detenerse un momento en el concepto de Magnitudes directamente proporcionales. No obstante, antes de continuar con esta definición, puede que sea necesario el traer a capítulo el concepto de Magnitudes, la cuales han sido explicadas de forma general como el conjunto de elementos, que cuentan con la propiedad de sumarse, compararse y ordenarse.

Con respecto entonces a las Magnitudes directamente proporcionales, se tendrá también que estas han sido explicadas como el conjunto de magnitudes, en donde se cumple la propiedad de que si una de ellas es multiplicada por un factor o número, las otras también. Sin embargo, es probable que la mejor manera de entender este concepto sea a través de un ejemplo concreto, tal como el que se muestra a continuación:

Si se en un tienda de telas se ofertara 1 metro de terciopelo por tan solo 4 euros, ¿en cuánto se podrían adquirir 5 metros de este material?

Al ser identificadas como Magnitudes directamente proporcionales, en tanto que si aumenta una de ellas, la otra también en igual cantidad, la solución de este problema puede darse entonces de dos formas: o se multiplica tanto los metros como el precio por 5, que es el factor que debe despejarse, o simplemente se hace un ejercicio de regla de tres simple directa, puesto que todo conjunto de magnitudes directamente proporcionales establecen entre ellas también proporciones:

1 metro → 4 euros
5 metros →  20 euros

Repartos directamente proporcionales

Por último, será también necesario detenerse en la definición de Repartos directamente proporcionales, los cuales han sido explicados como aquellos procedimientos matemáticos dirigidos a establecer en qué forma debe ser repartido justa o proporcionalmente un elemento dentro de un conjunto de elementos. Este tipo de problemas son bastante útiles en la vida diaria, por ejemplo cuando de un total de dinero, pagado por un trabajo, se necesita establecer qué monto le corresponde a cada uno de los trabajadores, según su producción u horas trabajadas.

Utilizando la regla de tres en repartos directamente proporcionales

Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre cómo pueden resolverse problemas de repartos directamente proporcionales, usando la regla de tres. Sin embargo, puede que la forma más idónea de abordar esta explicación, sea a través de un ejemplo concreto, tal como el que se muestra a continuación:

Si en una carpintería, se realizaron 6 mesas, con un valor de 600 euros, y en el trabajo participaron tres carpinteros, quienes fabricaron proporcionalmente las siguientes cantidades de mesas: Mario hizo 3, Juan, 1 y Ricardo, 2, ¿cuánto debería recibir cada uno de ellos por su trabajo realizado?

Se tendrá en primer lugar que revisar la información con la que se cuenta, y que se mostrará de la siguiente manera:

6 mesas → 600 euros

Mario → 3 mesas
Juan → 1 mesa
Ricardo → 2 mesas

En este caso, recordando que todo problema de regla de tres, establecido entre magnitudes directamente proporcionales, responde también a la primera ley de la proporción, se buscará entonces sacar razones de las magnitudes, siendo la primera la conformada por la cantidad de dinero ganado por las mesas y el total de mesas fabricadas:

Si por cada trabajador se estableciera una razón entre el monto que debe cobrar, el cual no se conoce, y funcionaría como antecedente de la razón, y el número de mesas que fabricó, y que serviría como consecuente, se tendrían que entre estas y la obtenida por el total se pudieran establecer a su vez proporciones, que dieran como resultado, mediante la regla de tres directa simple, el total que le corresponde cobrar a cada trabajador:

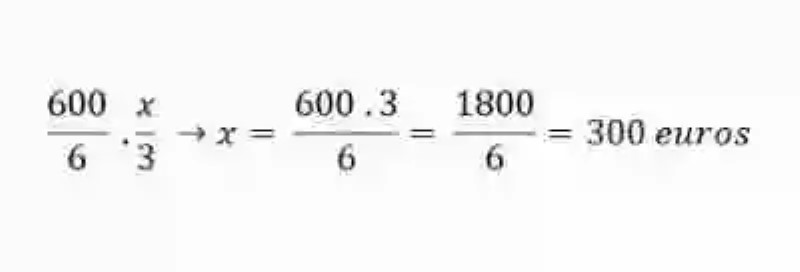
Proporción Mario:

Proporción Juan:

Proporción Ricardo:

Se tiene entonces que el dinero debe ser repartido proporcionalmente de la siguiente manera:

Mario → 300 euros
Juan → 100 euros
Ricardo → 200 euros

Imagen: pixabay.com