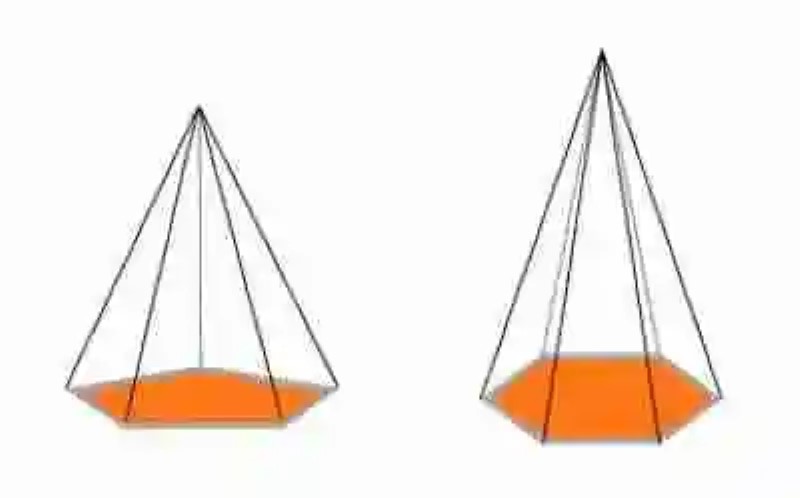
Quizás lo mejor, antes de abordar una explicación sobre el volumen de las pirámides, sea revisar de forma breve algunas definiciones, que de seguro permitirán entender este tipo de medida dentro de su contexto geométrico específico.
Definiciones fundamentales
Por consiguiente, puede que también sea recomendable delimitar esta explicación a cuatro nociones específicas: Polígonos, Triángulos, Poliedros y Pirámides, por encontrarse directamente relacionadas con la medida que se abordará posteriormente. A continuación, cada una de estas definiciones:
Los polígonos
De esta manera, se comenzará por decir que los Polígonos han sido descritos por los Polígonos como un tipo de figura geométrica, que se caracteriza por ser totalmente plana, o bidimensional, es decir, por contar tan solo con dos dimensiones, alto y ancho, sin que en ellas pueda encontrarse la tercera dimensión: la de la profundidad.
Así mismo, los polígonos han sido descritos como figuras completamente cerradas, las cuales se encuentran delimitadas por un conjunto de segmentos de recta, elementos estos que le otorgan a los polígonos otra de sus características básicas: la de contar con todos sus lados rectos. Por otro lado, la disciplina geométrica también señala que los Polígonos se encontrarán conformados por cuatro distintos elementos: lados, vértices, ángulos y diagonales.
Triángulos
En segunda instancia, será también necesario tomar un momento para pasar revista sobre la definición que da la Geometría respecto a los Triángulos, los cuales son considerados como uno de los principales tipos de polígonos que existen, así como una figura geométrica plana y completamente cerrada, la cual se encuentra delimitada por tres lados rectos. Así también, en los Triángulos existen varios elementos: tres lados, tres vértices, tres ángulos y no hay diagonales, debido a que para que existan en realidad deben disponerse entre vértices no contiguos, elementos que no existen tampoco en los triángulos.
Poliedros
Por igual, la Geometría indica que los Poliedros pueden ser considerados como espacios geométricos, que se encuentran completamente delimitados por un conjunto de polígonos. Así mismo, esta disciplina ha señalado que en los Poliedros se pueden encontrar también varios elementos, entre los que se encuentran las caras, aristas, vértices, ángulos diedros y ángulos poliedros.
Pirámides
Finalmente, también será necesario lanzar luces sobre la definición de Pirámides, las cuales serán vistas como un tipo de poliedro, es decir, como un espacio geométrico, que se encuentra delimitado por un conjunto de polígonos. En el caso específico de las pirámides, estos poliedros contarán con tres características específicas:
- contará con un conjunto de caras verticales, constituidas por triángulos.
- en segundo lugar, estos poliedros tendrán un vértice superior, en donde se encontrarán todos los triángulos que constituyen sus caras verticales.
- finalmente, en las pirámides también existirá una base, la cual puede estar conformada por polígonos distintos al triángulo. El número de lados que tenga cada polígono que se establezca como base, determinará el apellido de la pirámide: pirámide triangular, pirámide cuadrangular, etc.
Volumen de la pirámide
Una vez se han revisado cada uno de estos casos, puede que ciertamente sea mucho más sencillo abordar una explicación sobre el Volumen de la pirámide, el cual es entendido como una medida o propiedad geométrica, que da cuenta sobre el espacio que ocupa una pirámide determinada en un espacio específico.
Así mismo, la Geometría ha señalado que el Volumen de una pirámide en realidad resulta igual a un tercio del producto del área de la base por la altura. El área de la base, por cierto, se calculará según la fórmula que corresponda al tipo de polígono que constituye esta área de la pirámide. Esta relación geométrica para determinar el Volumen de este tipo de poliedro podrá expresarse a través de la siguiente fórmula:
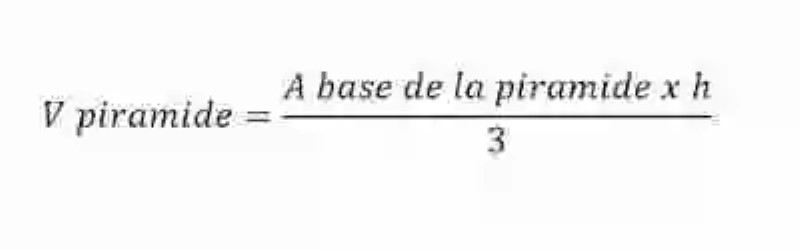
Imagen: wikipedia.org
El pensante.com (septiembre 30, 2018). Volumen de la pirámide. Recuperado de https://elpensante.com/volumen-de-la-piramide/